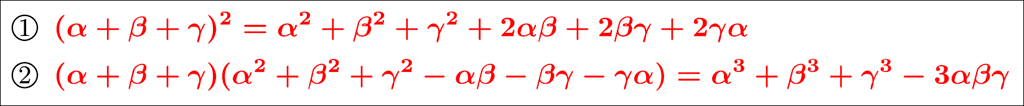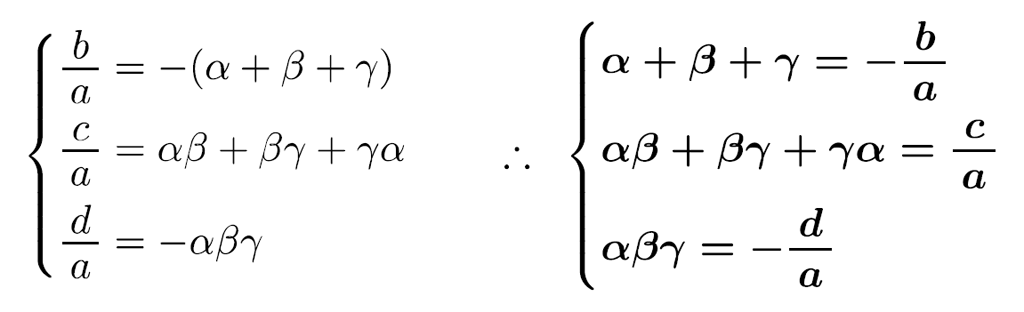以前の連載記事『大山壇の入試問題Pick Up !』とテーマが重複することもあるかもしれませんが,主に高校生・大学受験生に向けた内容にしていきます。生徒のみなさんにとっての演習に,先生方にとっては日々の指導の参考に,少しでも役立てば幸いです。
前回に続いて第2回も「対称式」がテーマです。
基本的な対称式計算は前回確認したので,今回は文字が増えたり,対称式が関係する応用問題にチャレンジです。頑張ってみてください!
2.1 3文字の対称式
前回は \(\alpha\) と \(\beta\) の2文字の対称式計算を扱いました。今回は3文字の対称式を扱いたいと思います。
3文字の場合の基本対称式は
\(\alpha+\beta+\gamma\),\(\quad \alpha\beta+\beta\gamma+\gamma\alpha\),\(\quad \alpha\beta\gamma\)
の3つになります。つまり,3文字の対称式はこの3つの基本対称式の四則演算で表せるということです。
さて,3文字の対称式計算でよく使う公式を2つ紹介しておきましょう。
どちらも,左辺を展開・整理すれば右辺になるので,各自で確認してみてください。
なお,②を右辺から左辺に変形する(因数分解する)のも良い計算練習になります。大山は次のように変形しています。
まず(前回扱った)
\(\alpha^{3}+\beta^{3}=(\alpha+\beta)^{3}-3\alpha\beta(\alpha+\beta)\) …… \((*)\)
を適用し,その後,順番を入れ替えて
\(\begin{aligned}& {\color{#0693e3}{\alpha^3 + \beta^3}}+ \gamma^3 – 3\alpha\beta\gamma \\[5pt]
&= {\color{#0693e3}{(\alpha + \beta)^3 – 3\alpha\beta(\alpha + \beta)}} + \gamma^3 – 3\alpha\beta\gamma \\[5pt]
&= (\alpha + \beta)^3 + \gamma^3 – 3\alpha\beta(\alpha + \beta) – 3\alpha\beta\gamma
\end{aligned}\)
とできます。さらに,\((\alpha+\beta)^{3}+\gamma^{3}\) の部分に再び \((*)\) を適用し,その後あれこれすると
\(\begin{aligned} & \alpha^{3}+\beta^{3}+\gamma^{3}-3\alpha\beta\gamma \\[5pt]
& =(\alpha+\beta)^{3}-3\alpha\beta(\alpha+\beta)+\gamma^{3}-3\alpha\beta\gamma \\[5pt]
&= {\color{#0693e3}(\alpha+\beta)^{3}+\gamma^{3}}-3\alpha\beta(\alpha+\beta)-3\alpha\beta\gamma \\[5pt]
&= {\color{#0693e3}\{(\alpha+\beta)+\gamma \} ^{3}-3(\alpha+\beta)\gamma \{(\alpha+\beta)+\gamma \} } -3\alpha\beta(\alpha+\beta)-3\alpha\beta\gamma \\[5pt]
&=(\alpha+\beta+\gamma)^{3}-3(\alpha+\beta)\gamma(\alpha+\beta+\gamma)-3\alpha\beta(\alpha+\beta+\gamma) \\[5pt]
&=(\alpha+\beta+\gamma) \{(\alpha+\beta+\gamma)^{2}-3(\alpha+\beta)\gamma-3\alpha\beta\} \\[5pt]
&=(\alpha+\beta+\gamma)(\alpha^{2}+\beta^{2}+\gamma^{2}+2\alpha\beta+2\beta\gamma+2\gamma\alpha-3\alpha\beta-3\beta\gamma-3\gamma\alpha) \\[5pt]
&=\boldsymbol{(\alpha+\beta+\gamma)(\alpha^{2}+\beta^{2}+\gamma^{2}-\alpha\beta-\beta\gamma-\gamma\alpha)}\end{aligned}\)
となります。
では,上記の2つの公式を使う練習をしてみましょう。
(2)の \(a^{3}+b^{3}+c^{3}\) を,前回の2文字と同様に \((a+b+c)^{3}\) からツジツマを合わせようとすると,なかなかにメンドウです。そこで,上記の公式②が有効です♪
(3)の「存在しないこと」の証明には背理法が有効であることが多いので,まず「存在する」と仮定してみましょう。(解答例はこちら)
また,上の公式②に関連する問題として,このような出題もありました。
(1)(2)ともに
\(a^{3}+b^{3}-c^{3}+3abc=a^{3}+b^{3}+(-c)^{3}-3ab\cdot(-c)\)
と考えれば,公式②が使えますね♪(解答例はこちら)
2.2 対称式と方程式
前回と同様,\(\alpha,\beta,\gamma\) を解とする3次方程式 \(ax^{3}+bx^{2}+cx+d=0\) を考えてみましょう。
方程式の両辺を \(a\) で割って
\(x^{3}+\cfrac{b}{a}x^{2}+\cfrac{c}{a}x+\cfrac{d}{a}=0\)
とでき,これの解が \(\alpha,\beta,\gamma\) なので,方程式の左辺は
\(x^{3}+\cfrac{b}{a}x^{2}+\cfrac{c}{a}x+\cfrac{d}{a}=(x-\alpha)(x-\beta)(x-\gamma)\)
と因数分解でき,この右辺を展開することで
\(\begin{aligned} & x^{3}+\cfrac{b}{a}x^{2}+\cfrac{c}{a}x+\cfrac{d}{a} \\
& =x^{3}-(\alpha+\beta+\gamma)x^{2}+(\alpha\beta+\beta\gamma+\gamma\alpha)x-\alpha\beta\gamma\end{aligned} \)
という恒等式が成り立ちます。よって,係数を比較して
が成り立ちます。これが,3次方程式の解と係数の関係です。
前回も書いたように,大山はこれの丸暗記を推奨していません。上記のように因数分解から作れるように練習しておきましょう!
ところで,上記の内容から,方程式
\(x^{3}-(\alpha+\beta+\gamma)x^{2}+(\alpha\beta+\beta\gamma+\gamma\alpha)x-\alpha\beta\gamma=0\)
の解が \(\alpha,\beta,\gamma\) なので
\(\begin{eqnarray} \left\{ \begin{array}{l} \alpha^{3}-(\alpha+\beta+\gamma)\alpha^{2}+(\alpha\beta+\beta\gamma+\gamma\alpha)\alpha-\alpha\beta\gamma=0\\\beta^{3}-(\alpha+\beta+\gamma)\beta^{2}+(\alpha\beta+\beta\gamma+\gamma\alpha)\beta-\alpha\beta\gamma=0\\\gamma^{3}-(\alpha+\beta+\gamma)\gamma^{2}+(\alpha\beta+\beta\gamma+\gamma\alpha)\gamma-\alpha\beta\gamma=0 \end{array} \right. \end{eqnarray}\)
すなわち
\(\begin{eqnarray} \left\{ \begin{array}{l} \alpha^{3}-\alpha\beta\gamma=(\alpha+\beta+\gamma)\alpha^{2}-(\alpha\beta+\beta\gamma+\gamma\alpha)\alpha\\\beta^{3}-\alpha\beta\gamma=(\alpha+\beta+\gamma)\beta^{2}-(\alpha\beta+\beta\gamma+\gamma\alpha)\beta\\\gamma^{3}-\alpha\beta\gamma=(\alpha+\beta+\gamma)\gamma^{2}-(\alpha\beta+\beta\gamma+\gamma\alpha)\gamma\end{array} \right. \end{eqnarray}\)
が成り立ちます。この3式を加えることで
\(\begin{aligned} & {\color{#ff0000}\alpha^{3}+\beta^{3}+\gamma^{3}-3\alpha\beta\gamma} \\[5pt]
& =(\alpha+\beta+\gamma)(\alpha^{2}+\beta^{2}+\gamma^{2})-(\alpha\beta+\beta\gamma+\gamma\alpha)(\alpha+\beta+\gamma) \\[5pt]
& =(\alpha+\beta+\gamma)\{(\alpha^{2}+\beta^{2}+\gamma^{2})-(\alpha\beta+\beta\gamma+\gamma\alpha)\} \\[5pt]
& ={\color{#ff0000}(\alpha+\beta+\gamma)(\alpha^{2}+\beta^{2}+\gamma^{2}-\alpha\beta-\beta\gamma-\gamma\alpha)}\end{aligned} \)
と,2.1で紹介した公式を作ることができます♪
さて,前回同様
基本対称式の値が分かっていれば,\({\color{#0693e3}\boldsymbol{\alpha}}\) と \({\color{#0693e3}\boldsymbol{\beta}}\) と \({\color{#0693e3}\boldsymbol{\gamma}}\) を解とする3次方程式を作れる
ということなので,このことを利用するのが次のような問題です。
(2)では,直方体の3辺の長さを \(\alpha,\beta,\gamma\) とおき,体積を \(V\) とすれば,(1)を利用できることに気付けるはずです。ここで注意しなければいけないのが,「 \(\alpha,\beta,\gamma\) はすべて正の実数でなければいけない」ということです。(解答例はこちら)
そして,次の問題はこちら。
点 \((s+t,st)\) が動く領域の図示なので
\(X=s+t,Y=st\)
とおいて,\({\color{#0693e3}\boldsymbol{X}}\) と \({\color{#0693e3}\boldsymbol{Y}}\) の関係式を作ることが目標です。
しかし,ここで,見えている条件式 \(s^{2}+t^{2}\leqq6\) に飛びついて
\((s+t)^{2}-2st\leqq6\quad \therefore\quad X^{2}-2Y\leqq6\)
とするだけではダメなのです。例えば,点 \((0,1)\) は
\(0^{2}-2\cdot1=-2\leqq6\)
なので,条件 \(X^{2}-2Y\leqq6\) を満たしますが
\(\begin{eqnarray} \left\{ \begin{array}{l}s+t=0 \\ st=1\end{array} \right. \end{eqnarray}\)
とすると,\(s,t\) を解とする \(x\) の方程式が
\(x^{2}-0x+1=0\quad \therefore\quad x^{2}+1=0\)
となり,この解は \(x=\pm i\) なので実数ではありません。
つまり,適切な実数 \(\boldsymbol{s,t}\) が存在しないということになります。(1)は「気付いてね」という出題者のメッセージなのでしょう。
というわけで,\(X=s+t,Y=st\) という置き換えをしたときには(他にも色々な場合がありますが),実数 \(\boldsymbol{s,t}\) の存在条件を考える必要があるわけです。入試においては頻出なので,しっかりと理解しておきましょう!
一般的に,軌跡・領域を求めるときには,パラメータの存在条件を考えることが大切なのですが,それはまた別の機会にお話ししたいと思います。(解答例はこちら)
第2回は以上になります。前回より少しレベルの高い内容になっていましたが,理解できましたか?
次回は,「関数の最大・最小」について基本から確認したいと思います。それでは,また!
宇都宮北高校,東北大学理学部数学科卒。
2006年度から代々木ゼミナールの講師となり,現在は新宿本部校と札幌校に出講しています。対面・映像の授業の他にも,テキスト・模試・解答速報の作成なども行っています。
もっと毒をはいている大山を見たい方は,X(旧Twitter)をどうぞ!→ @dan_oyama_0206
《著書》
・『全国大学入試問題正解』(旺文社)解答執筆(京大,一橋大,東北大など)
・『整数 分野別標準問題精講』(旺文社)
・『全レベル問題集③』(旺文社)
・『全レベル問題集⑤』(旺文社)
・『大山壇の基本から身につける計算力IA』(KADOKAWA)
・『大山壇の基本から身につける計算力IIB』(KADOKAWA)
その他のコンテンツ