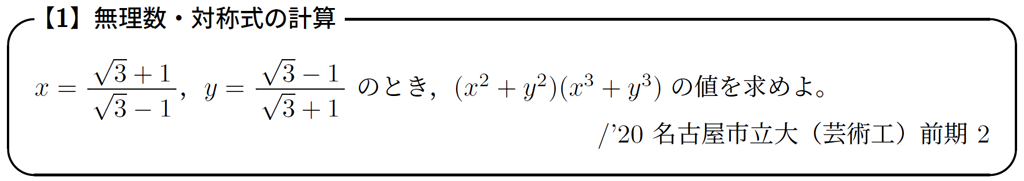以前の連載記事『大山壇の入試問題Pick Up !』とテーマが重複することもあるかもしれませんが,主に高校生・大学受験生に向けた内容にしていきます。生徒のみなさんにとっての演習に,先生方にとっては日々の指導の参考に,少しでも役立てば幸いです。
皆さん,こんにちは!
第1回の今回は「対称式」がテーマです。数学は何だかんだ言っても「計算力」が大切です。方針が見えて,立式もできたけど,計算ができなくて最終結果までたどり着けなかったという経験が誰にでもあるでしょう。そういうことを減らす為にも,計算力を鍛えることはとても大切です。
いろいろな計算がある中で,今回は「対称式」をpick up したいと思います。
1.1 対称式の計算
\(\alpha^2+\beta^2\) や \(\alpha-\alpha^3 \beta^3 +\beta\) などのように,式中のどの2文字を交換しても式全体は変わらない式のことを対称式と言います。
特に,対称式の中でも基本となる式
\(\alpha+\beta\)(和),\(\alpha \beta\) (積)
を(そのままですが)基本対称式と言い
すべての対称式は基本対称式の四則演算で表せる
ことが知られています。
例えば
\(\alpha+\beta=3\),\(\alpha \beta=1\) のとき,\(\alpha^2+\beta^2\) の値を知りたい
としましょう。
この2 式を「\(\alpha\),\(\beta\) についての連立方程式」と見て解くと…
\(\alpha+\beta=3\) から \(\beta=3-\alpha\) なので
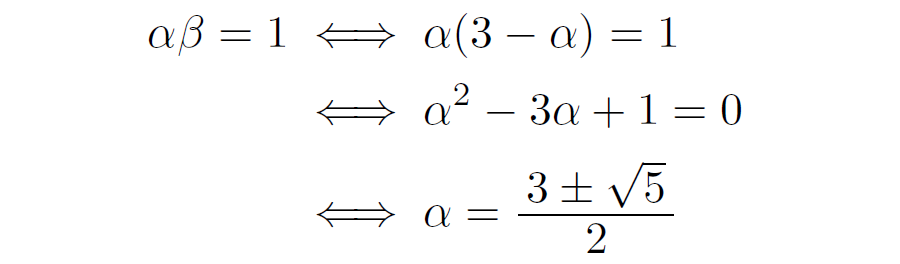
\(\beta=3-\alpha\) だから
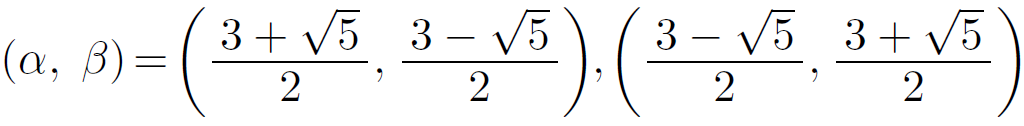
となります。これらの値を代入することで(2組のどちらの場合でも)
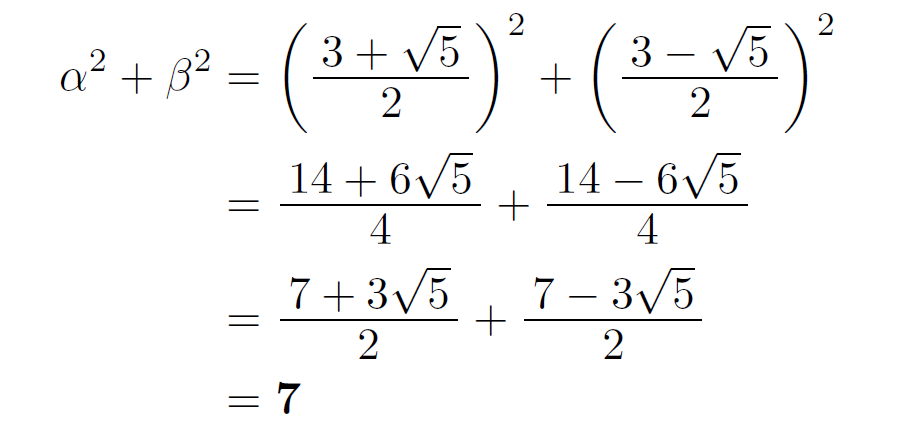
と,結果を得られますが,展開公式(因数分解公式)
\(\color{#ff0000}\boldsymbol{(\alpha+\beta)^2=\alpha^2+2\alpha \beta +\beta^2}\)
を利用して
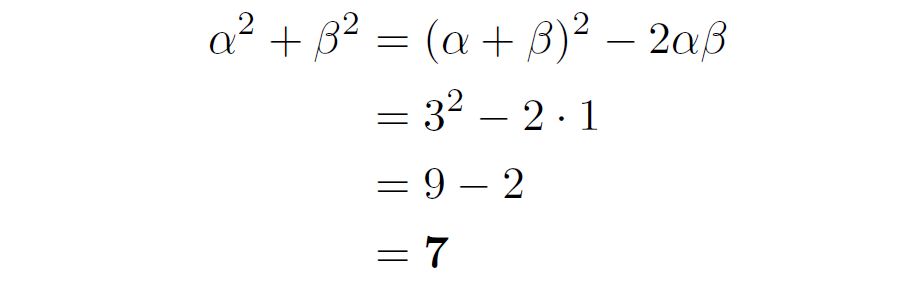
とする方が速くて安全です♪
\(\alpha^3+\beta^3\) も,公式
\(\color{#ff0000}\boldsymbol{(\alpha+\beta)^3=\alpha^3+3\alpha^2 \beta +3\alpha \beta^2+\beta^3}\)
を利用して
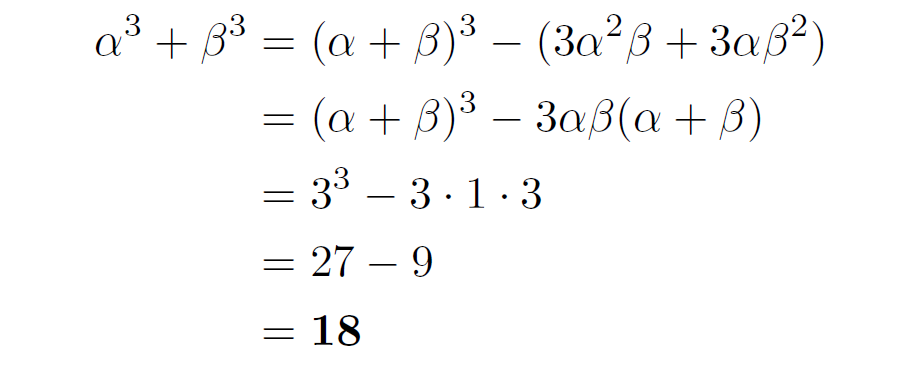
とできます。
このような対称式計算は,次のような無理数の計算にも有効です。
もちろん,直接代入して気合と根性で攻めることもできますが,求めるものが「対称式の値」なので
まず,基本対称式の値を求めておく!
と考えると,安全な計算に落とし込めます♪ (解答例はこちら)
続いて,次の問題はどうでしょう?
典型的な対称式計算に見えますが,求めるものが \(a^7+b^7\) という7次式になっているという点がポイントです。\(a^2+b^2\) や \(a^3+b^3\) なら,\((a+b)^2\),\((a+b)^3\) の展開式からツジツマを合わせれば良かったわけですが,\((a+b)^7\) の展開式から考えるのはメンドウです(できないわけではありません)。そこで,ひと工夫することを考えてみてほしいのです。(解答例はこちら)
1.2 対称式と方程式
\(x\) についての2次方程式 \(ax^2+bx+c=0\) すなわち \(x^2+\cfrac{b}{a}x+\cfrac{c}{a}=0\) の解が \(\alpha\) と \(\beta\)(重解は \(\alpha=\beta\) と考える)であるとき,方程式の左辺は
\(x^2+\cfrac{b}{a}x+\cfrac{c}{a}=(x-\alpha)(x-\beta)\) ………①
と因数分解でき,この右辺を展開することで
\(x^2+\cfrac{b}{a}x+\cfrac{c}{a}=x^2-(\alpha+\beta)x+\alpha \beta\)
という恒等式が成り立ちます。よって,係数を比較して
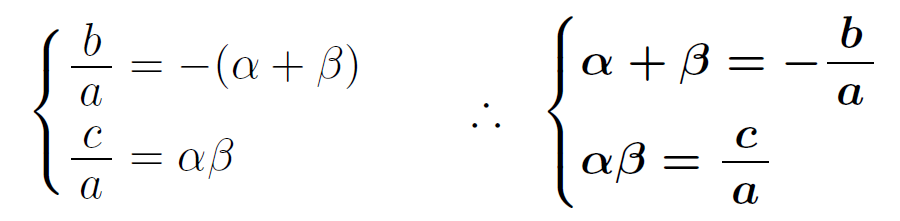
が成り立ちます。これを解と係数の関係と言います。
大山は,この結果を丸暗記することよりも,上の①式のように
解が分かれば因数分解できる♪
という考え方が大切だと思っています。丸暗記だと符号をミスしたり,3次方程式や4次方程式になると手を出せなくなってしまったりする可能性もありますが,因数分解から導出するようにしていれば大丈夫です。
さて,この解と係数の関係を見ると,基本対称式 \(\alpha+\beta\),\(\alpha \beta\) が出てきましたね。ということは
基本対称式の値が分かっていれば,\(\boldsymbol{\alpha}\) と \(\boldsymbol{\beta}\) を解とする2次方程式を作れる
ということです。
前節の例と同じ \(\alpha+\beta= 3\),\(\alpha \beta= 1\) を考えてみましょう。このとき,\(x\) の2次方程式で \(\alpha\) と \(\beta\) を解とするものを作ると
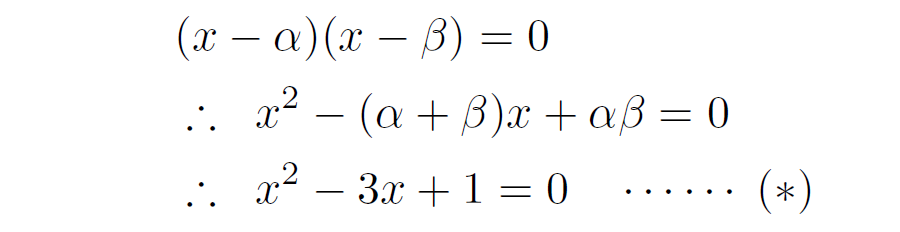
となります(他にも,この式の両辺に5をかけた \(5x^2-15x+5=0\) なども考えられますが,解が変わるわけではないので,ここでは重要ではありません)。
この方程式(*)の解が \(\alpha\),\(\beta\) なので
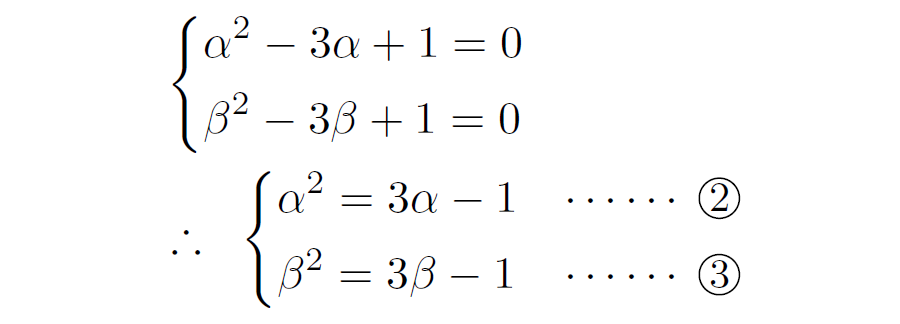
ここで②+③を考えると
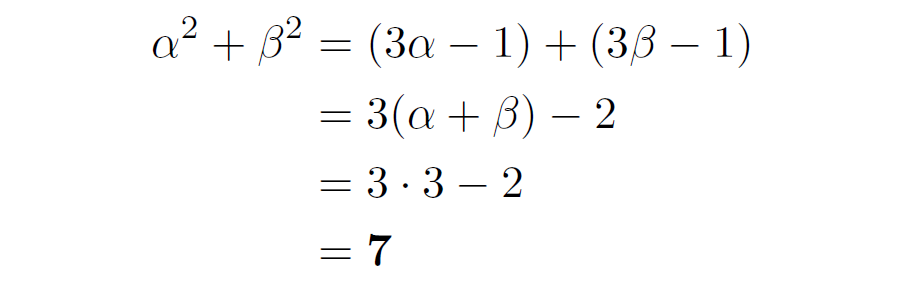
②× \(\alpha\) +③× \(\beta\) を考えれば
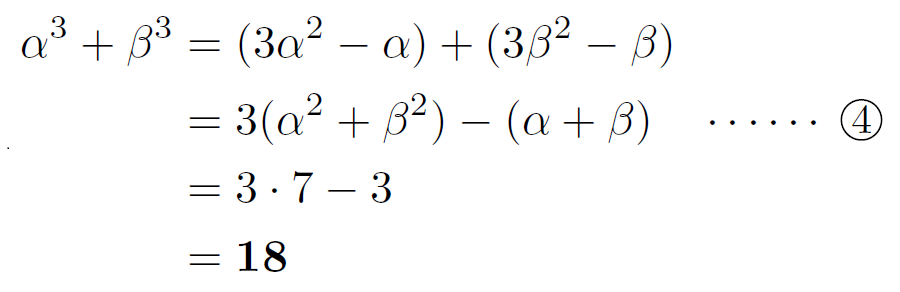
とできます。
②式は「\(\alpha^2\) を \(\alpha\) の1次式で表している」ことになるので,次数が下がり,扱いやすくなっています。このような計算を次数下げと言います。対称式の計算に限らず,方程式の解を代入したいときによく使う方法なので,ぜひ練習しておきましょう!
ところで,④式は「\(\alpha^3+\beta^3\) を \(\alpha^2+\beta^2\) と \(\alpha^1+\beta^1\) で表している」形になっているので,数列 \(\{ \alpha^n+\beta^n \} \) の漸化式がぼんやりと見えています。このことを踏まえて,次の問題を見てみましょう。
方程式 \(x^2-3x+5=0\) を解くと
\(x=\cfrac{3 \pm \sqrt{11}i}{2}\)
という虚数になってしまうので,この値を用いて証明するのは骨が折れそうです。そこで,一般項を
\(a_n=\alpha^n+\beta^n-3^n\)
とする数列 \(\{ a_n\}\) を設定し,数学的帰納法に持ち込むのが良さそうです。
ちなみに,数学的帰納法については以前の連載記事『大山壇の入試問題Pick Up!』でも 扱っているので,ぜひ読んでみてください!(解答例はこちら)
次の問題も同様に処理できますので,類題として練習してみましょう!
(4)で出てくる「互いに素」というのは,最大公約数が1という意味です。言い換えると, 「1 より大きな公約数は存在しない」ということなので,「存在する」と仮定して矛盾を導くのがセオリーです。つまり,背理法の出番です。(解答例はこちら)
第1回は以上になります。どうでしょうか。楽しんでいただけましたか?
次回は,今回の内容の続きとして「対称式にまつわるエトセトラ(その2)」を予定しています。お楽しみに♪
宇都宮北高校,東北大学理学部数学科卒。
2006年度から代々木ゼミナールの講師となり,現在は新宿本部校と札幌校に出講しています。対面・映像の授業の他にも,テキスト・模試・解答速報の作成なども行っています。
もっと毒をはいている大山を見たい方は,X(旧Twitter)をどうぞ!→ @dan_oyama_0206
《著書》
・『全国大学入試問題正解』(旺文社)解答執筆(京大,一橋大,東北大など)
・『整数 分野別標準問題精講』(旺文社)
・『全レベル問題集③』(旺文社)
・『全レベル問題集⑤』(旺文社)
・『大山壇の基本から身につける計算力IA』(KADOKAWA)
・『大山壇の基本から身につける計算力IIB』(KADOKAWA)
その他のコンテンツ