特集記事（高校）

　皆さん，こんにちは。大山です。
　最終回となる今回は，2025年度の入試問題から教科書から入試への橋渡しとなる問題を選んでみました。教科書の内容を一通り学んだ段階では，各単元の知識がバラバラになっていて，分野を越えた繋がりや複雑な問題への対応の仕方が見えている生徒はそう多くはありません。そんな生徒たちを少しずつステップアップさせるためにオススメの問題を4つ紹介します。

問題の特徴を理解する

　まず最初の問題はこちら。

 　\(f(x)=0\)は3次方程式ですが，因数分解されているので，2次方程式 \(x^2+2ax+b=0\) がどのような解をもてばよいかを考える問題です。実際に生徒たちに解かせてみると

などで混乱した答案がとても多いです。

　①，②は，「3次方程式は～するもの」というパターンマッチングで解いてきていて，目の前の問題の特徴を考えていないタイプ。
　③は，教科書レベルの単問は考えられるけど，複数の要素が絡んだ問題になると整理しき
れないタイプ。
　この①～③のタイプは，定期テストではそこそこの点数を取りますが，受験学年になってからの記述模試・共通テスト模試で思った通りに点数が取れなくなってしまうでしょう。
　④は，よく考えてはいるけど，記述答案を人に見てもらう（添削してもらう）という経験が少ないため，自分の答案を客観的に見ることができずに起こりやすい現象です（上位の大学を目指す浪人生に多い）。実力がなかなか点数に現れず，もったいないタイプですね。

　というわけで，受験生として学習してほしいことを色々と伝えられる一問になっていると思います。（解答例はこちら）

分野をまたいだ問題

　2問目は「確率漸化式」のド定番問題です。

　「確率漸化式」に慣れていない生徒たちに，最初の一問として解かせたい問題です。
　2点 \(\text{A，B}\) を移動する点 \(\text{P}\) の位置を追っていくことが，そのまま推移図（遷移図）に繋がるので漸化式への誘導がしやすく，また，点 \(\text{P}\) が \(\text{A}\) にある確率と \(\text{B}\) にある確率の和が1であることも理解しやすいので，スムーズに受け入れられやすいでしょう。

　よく「サイコロを \(n\) 回投げたときに出た目の総和が偶数である確率」などが確率漸化式の一問目として載っていたりしますが，これは「奇数の目が偶数回出る」と考える方が自然な発想なので，漸化式に持っていくこと自体がやや不自然です。したがって，名城大の問題のような「点の移動」の問題で確率漸化式を紹介してから，その有用性を他の問題で実感してもらうという流れの方が，大山は好みです。（解答例はこちら）

誘導の意味を捉える

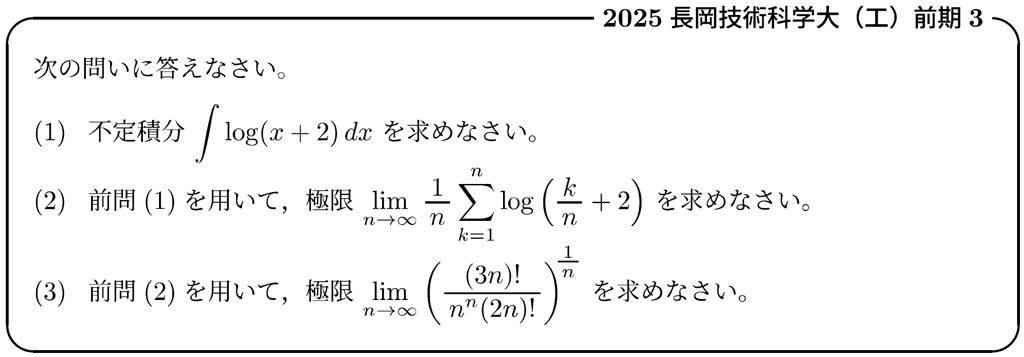
　3問目は「区分求積法」です。

　(3)の「対数をとってから区分求積」という問題は少しレベルが高いのですが，(1），(2）からの流れで初見でも想像しやすい構成になっています。

　例えば，いきなり(3)だけを生徒たちに解かせて，それで気づいたらもちろんOKだし，ヒントとして本間の全体を見せて改めて考えさせるなどの工夫も良いですね。
　ちなみに大山は，(2)の極限は \(\int_0^1 \log (x+2) dx\) とするのではなく，\(\int_2^3 \log x \!\ dx\) とする方が自然であると考えているので，この問題のそこだけは嫌いです（笑）（解答例はこちら）

図形の条件式の意味を考える

　最後は，複素数平面上の「図形の式」についての問題です。

　(1)は所謂「アポロニウスの円」と呼ばれる問題ですが，この式変形も苦手な生徒が多いですね。

　(2)は，「2つの条件をともに満たす \(z\)」を「2つの図形（円）の共有点」と見ることができれば(1)を利用できるのですが，\(xy\) 平面の話であれば慣れているこの議論も複素数平面では使えていない生徒が多いものです。また，\(a=1\) の場合を考えない，もしくは，\(a=1\) の場合の条件 \( | z-1 | = | -z+1 | \) が何を表しているのか分からない，という誤答が多発します。

　「図形の式」とは何か（前回の記事でも扱いました）を考えさせたい問題ですね。（解答例はこちら）

　最終回は以上になります。
　1年間にわたる連載は，締め切りに追われてメンドウなときもあったけど，自分の指導方針や問題選定の基準などを改めて言語化する良い機会でした。学校の教員をしている知人や，イベント授業などでお会いした先生方から「読んでるよ」「次が楽しみです」などと言ってもらえたり，ネット上で話題に上がっているのを見たりして，嬉しく思い，それが励みになり，執筆意欲に繋がりました。
　このような機会をくださった東京書籍の皆様，数多くの講師の中から大山に白羽の矢を立てた代ゼミの担当者，そして何よりも読者の皆様には感謝の気持ちしかありません。またいつか，お会いできる日が楽しみです。一年間，ありがとうございました♪