特集記事（高校）

　みなさん，こんにちは。今回は『場合の数』の指導時に大山が気を付けていることをお話ししたいと思います。

数えあげ

　この分野の一番の基本は数えあげです。樹形図や表を活用して数えあげることがまず大切なのですが，苦手な生徒ほど「どの公式を当てはめようか？」と考えてしまいがちです。
　したがって，指導者が樹形図や表を描くところを何度も何度も見せることが大切だと思います。指導者が最初から計算していたら，生徒たちも「最初から計算するもの」と思ってしまっても不思議ではありません。
　さて，今年の北大（文系）でこんな出題がありました。

　条件「 \(2\leqq a \lt b \lt c \leqq 6\) 」を満たす整数 \(a，b，c\) の組は \(_5\text{C}_3=10\) 組しかないので，全部書きあげても大したことはありません。（解答例はこちら）

選ぶと並べる

　大山はよく生徒たちに「何を1と数えているのかを理解しろ」と話します。つまり、例えば，\((A，B)\) と \((B，A)\) を同一視して「1通り」と数えるのか、それとも別物視して「2通り」と数えるのかを明確に区別してほしいということです。
　これを指導する為に大山が気を付けているのが，「選ぶ」と「並べる」の言葉の使い分けです。上記の例で言えば，\((A，B)\) と \((B，A)\) を同一視するときには「選ぶ」，別物視するときには「並べる」と表現しながら授業しています。ときには問題文を言い換えることも大切です。

• 男子3人，女子4人を両端に男子がくるように横一列に並べる
  → 左端の男子1人と右端の男子1人を選び，残りの5人をあいだに並べる

\(3\cdot 2\cdot 5!=3\cdot 2\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1=720\) （通り）

• 委員会のメンバー7人から，委員長、副委員長、書記の3人を選ぶ
  → 7人から3人を選んでから並べる

\(_7\text{C}_3\cdot 3!=\frac{7\cdot 6\cdot 5}{3\cdot 2\cdot 1}\cdot 3\cdot 2\cdot 1=210\) （通り）

　なお，大山は「 \(_n\text{P}_k\) 」を使いません。これは「選びながら並べる」計算です。上記のように「選んでから並べる」と指導する方が，生徒の理解度が高いと感じています。

　また，大山は「同じものを含む順列」を席選びと教えています。例えばこのように。

　このように教えておくと，あとで「反復試行の確率」や「二項定理」を教えるときに統一感があって，伝わりやすいです。

　とにかく、指導者側が「選ぶ」と「並べる」を意識的に使い分けることで，生徒たちの理度・再現度が高まります。
　さて，この「選ぶ」と「並べる」の練習にちょうど良い問題を2題紹介します。まずはこちら。

　シンプルな問題ですが、「この問題って \(\text{P}\) と \(\text{C}\) のどっちを使うの？」なんて考えている生徒に有効です！（解答例はこちら）

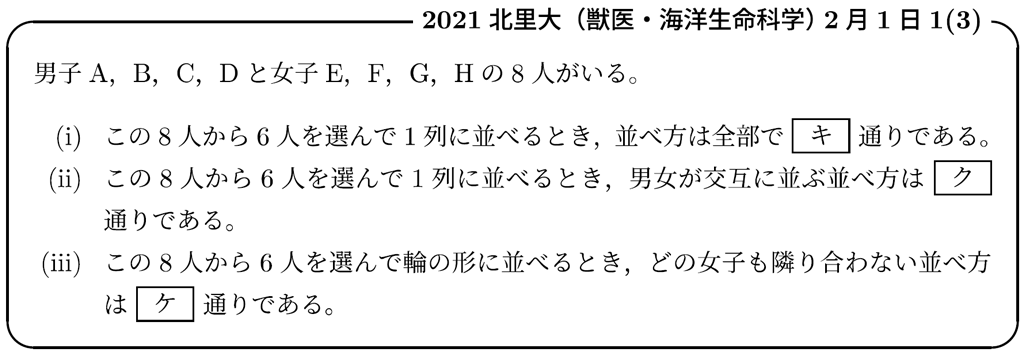
　そして次に，円順列も絡んだ問題がこちら。

　「隣り合わない」はあとからスキマに入れる作戦が有効です。（解答例はこちら）

　第8回は以上になります。『場合の数』と『確率』をまとめて書くつもりだったのですが，思ったよりも長くなりそう（苦笑）なので、今回は『場合の数』だけにしました。
　したがって，次回は今回の続きとして『確率』について書きます。お楽しみに♪