特集記事（高校）

　コンビニやスーパーの弁当に次のようなラベルが貼ってありました。電子レンジ \(500\text{W}\) で1分30秒，つまり90秒温めると適切な温度になっておいしくいただけることを意味しています。

【疑問】 電子レンジ \(500\text{W}\) で90秒温めるとき，\(500\times 90=45000\) は何の数値を表しているのでしょう。

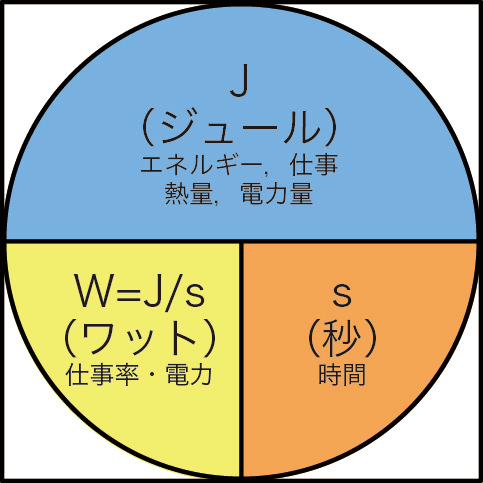
【答え】 \(\text{W}\) は単位ワット（Watt）で，1秒 \([\text{s}]\) に1ジュール \([\text{J}]\) の仕事（エネルギー，熱量，電気量）が行われるときの仕事率（仕事の変化率）と定められています。
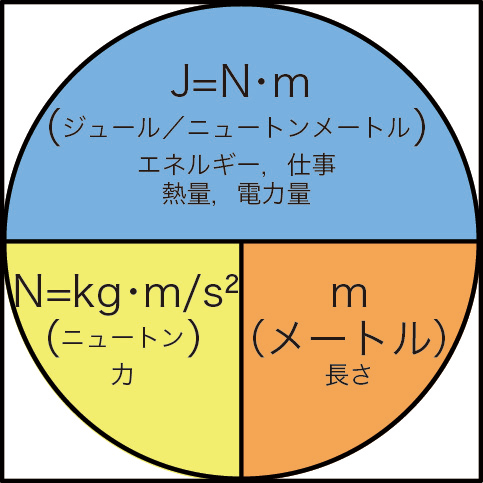
　単位だけ書くと，\(\text{W}=\text{J}/\text{s}\) と定義されます。これより，\(\text{J}=\text{W}\cdot \text{s}\) という単位の関係がわかります。よって，\(500\text{W}\times90\text{s}=45000\text{J}\) という意味になります。つまり，弁当に \(45000\text{J}\) の熱量を与えて，温めることになります。

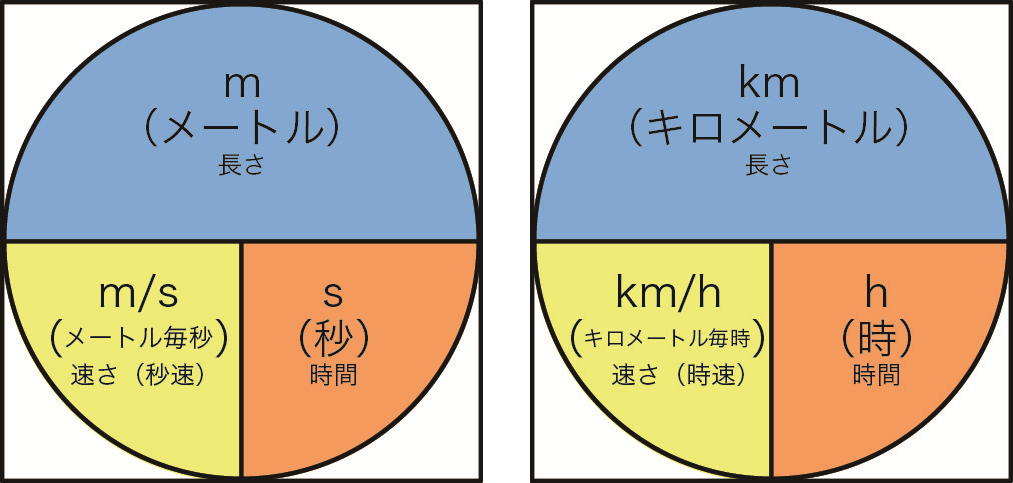
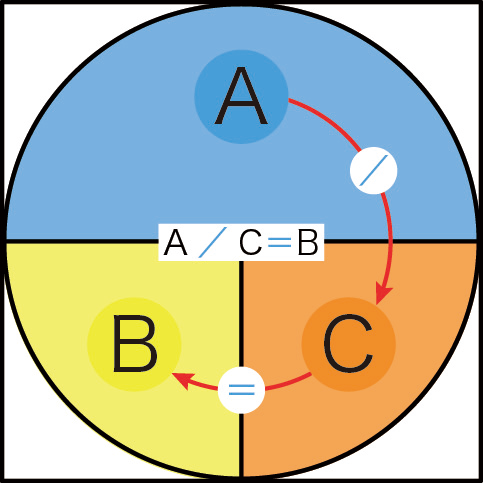
【注意】 \(\text{W}=\text{J}/\text{s}\) の関係は，下図のような，\((\text{速さ})=(\text{長さ})/(\text{時間})\)の関係と同じですね。

　なお，キロ（kilo）は，基本単位の1000倍（10の3乗倍）という意味です。例えば， \(1\text{km}=1000\text{m}\) であり，\(45000\text{J}=45\text{kJ}\) です。　
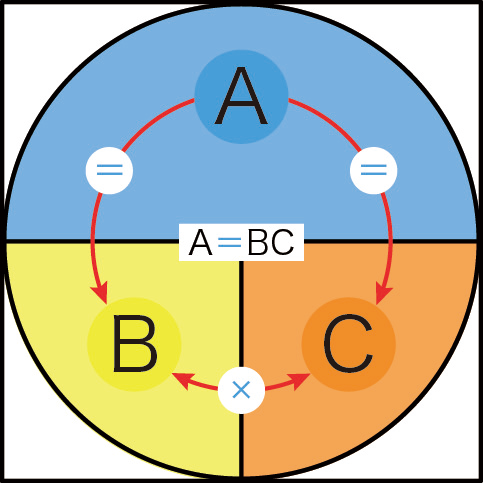
　この図の一般的な見方は，下図のように，量Aが量Bと量Cの積に等しいと見ます。

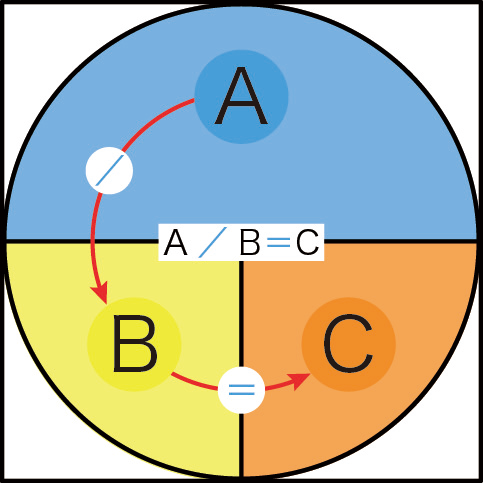
　したがって，量A÷量Bは量Cに等しくなります。

　あるいは，量A÷量Cは量Bに等しいことになります。

【疑問の深掘り】
　\(45\text{kJ}\) の熱量を与えると弁当はどのくらい温まるのでしょうか？

【答え】 物質の温度を1℃上げるのに必要な熱量を熱容量，物質 \(1\text{g}\) あたりの熱容量を比熱（比熱容量）と呼びます。
　熱量の単位カロリー \([\text{cal}]\) と，セルシウス温度の単位セルシウス度[℃]の代わりに絶対温度の単位ケルビン \([\text{K}]\) を使って，例えば，水の比熱は \(1\text{cal}/(\text{g}\cdot\text{K})\) となります。（温度間隔1℃と \(1\text{K}\) は等しいです。）
　実は，比熱は水の温度によって変わるので，カロリーを単位にすると定義としては値にぶれが生じることから，熱量の単位は国際的にジュールに統一されています。（ただし，日本では人や動物が摂取する物の熱量などについてだけはカロリーが用いられています。）

　カロリーとジュールの関係は，\(1\text{cal}=4.184\text{J}\) と厳密に変換の数値が定められています。例えば，水 \(1\text{g}\) を標準大気圧の下で14.5℃から15.5℃に上げるのに必要な熱量は約 \(4.1855\text{J}\) です。19.5℃から20.5℃に上げるには約 \(4.182\text{J}\) の熱量が必要です。ちなみに，20℃の空気の比熱は約 \(1\text{J}/(\text{g}\cdot\text{K})\)，プラスチックは \(1.5\text{J}/(\text{g}\cdot\text{K})\) 程度です。比熱が大きい物質は温まりにくい（冷めにくい）です。

　さて，疑問の深掘りに答えましょう。ある温度の水の比熱がちょうど

\(c=1\text{cal}/(\text{g}\cdot\text{K})=4.184\text{J}/(\text{g}\cdot\text{K})\)

であったとします。この水 \(500\text{ml}\) に \(45\text{kJ}\) の熱量を与えたら \(\varDelta T\) だけ温度が上昇したとします。\(500\text{ml}\) の水は \(500\text{g}\) ですから，\(45\text{kJ}=500\text{g}\times c\times\varDelta T\) から，\(\varDelta T=45000\text{J}/(500\text{g}\times \text{c})\fallingdotseq 21.5\text{K}\) だけ温度が上がります。
　実際は，弁当箱ごと熱量を与えて，弁当の容器の比熱や具材によって温度上昇の程度が変わるので，正確な値はわかりませんが，大雑把にいって，電子レンジ \(500\text{W}\) で90秒温めると20℃くらいは温度が上がると思ってよいでしょう。

※\(\varDelta T\) は温度差を表す記号として使いました。\(\varDelta T\) の \(T\) は温度temperatureの頭文字の大文字です。（小文字の \(t\) は時間timeの頭文字として使うことが多いです。）また，\(\varDelta\) はアルファベットの \(d\) に対応するギリシャ文字 \(\delta\)（デルタ，delta）の大文字です。\(d\) は差differenceの頭文字です。\(dT\) と書くと \(T\) の微分differentialの意味になりますので，差や増分を表すときには通常 \(\varDelta T\) と書きます。

【疑問】 以下のラベルが貼ってある弁当を電子レンジ \(900\text{W}\) で温めたい場合，適切な温め時間は何分何秒でしょうか。

【答え】 ラベルに従うと電子レンジで

\(500\text{W}\times 180\text{s}=1500\text{W}\times 60\text{s}=90000\text{J}=90\text{kJ}\)

の熱量を与えることになります。よって，\(900\text{W}\) で温める場合は，\(90\text{kJ}/900\text{W}=100\text{s}\)，つまり1分40秒です。

【疑問】 以下のラベルが貼ってある弁当を電子レンジ \(900\text{W}\) で温めたい場合，適切な温め時間は何分何秒でしょうか。

【答え】 ラベルに従うと電子レンジ \(500\text{W}\) で \(500\text{W}\times 240\text{s}=120\text{kJ}\) の熱量を与えますが，\(1600\text{W}\) だと \(1600\text{W}\times 70\text{s}=112\text{kJ}\) の熱量を与えることになります。よって，\(500\text{W}\) の方の熱量を採用すると，\(900\text{W}\) で温める場合は \(120\text{kJ}/900\text{W}\fallingdotseq 133\text{s}\) ですが，電子レンジの温め時間が10秒おきにしか設定できない場合，2分10秒〜2分20秒です。
　一方，\(1600\text{W}\) の方の熱量を採用すると，\(112\text{kJ}/900\text{W}\fallingdotseq 124\text{s}\) なので，2分〜2分10秒です。ふたつの間をとって，2分10秒くらいが妥当でしょうか。

※ワット数によって熱量が異なる理由はこのラベルの弁当が置いてある店に設置してある業務用電子レンジの設定が \(1600\text{W}\) だからだと思われます。仮に \(1600\text{W}\) で1分20秒の温め時間とすると，熱量は \(128\text{kJ}\) となって，\(500\text{W}\) のときの熱量を超えてしまいます。したがって，\(500\text{W}\) の熱量を基準とすると，温め過ぎになってしまいます。

ジュールの贈り物

　ジュール \([\text{J}]\) は，イギリスの物理学者ジェームズ・プレスコット・ジュール（James Prescott Joule，1818－1889）にちなんだ，エネルギー，仕事，熱量，電気量の単位である。
　上述したように20℃の空気の比熱は約 \(1\text{J}/(\text{g}\cdot\text{K})\) である。ある温度の水の比熱がちょうど \(4.184\text{J}/(\text{g}\cdot\text{K})=1\text{cal}/(\text{g}\cdot\text{K})\) だったとすると，その水 \(1\text{g}\) の温度を \(1/4.184\fallingdotseq 0.24\) ℃上げるのに必要な熱量が \(1\text{J}\) である。つまり，\(1\text{J}\) の熱を与えると，空気の温度は1℃上がるが，水の温度は0.24℃しか上がらないから，水の方が温まりにくいことがわかる。

　ジュール \([\text{J}]\) は，仕事の単位でもあるので，\(1\text{J}\) は 1ニュートン \([\text{N}]\) の力で物体を \(1\text{m}\) 動かしたときの仕事の大きさに等しい。ニュートンは力の単位で，質量 \([\text{kg}]\) と加速度 \([\text{m}/\text{s}^2]\) の積の単位である：\(\text{N}=\text{kg}\cdot\text{m}/\text{s}^2\) 。これより，単位の関係は，\(\text{J}=\text{N}\cdot\text{m}=\text{kg}\cdot(\text{m}/\text{s})^2\) となる。（質量と速度の2乗の積）
　\(1\text{N}\) の力というのはわかりづらいが，重力加速度が \(g=9.8\text{m}/\text{s}^2\) なので，\(1\text{N}/g\fallingdotseq 102\text{g}\) の物体にかかる重力であり，それを \(1\text{m}\) 持ち上げると \(1\text{J}\) の仕事をしたことになる。キウイ1個が \(100\text{g}\) 程度である。

　ジュールは，おもりを降下させ，滑車を通して水を攪拌し，水の温度を上昇させるという実験をおこなった。これより，仕事（エネルギーの増加）が温度上昇と等しいことを看破した。つまり，力学的エネルギーが熱エネルギーに変換されるということである。
　例えば，\(100\text{m}\) の高さから落ちる滝において，\(100\text{m}\) の高さにある \(1\text{kg}\) の水の塊の位置エネルギー \(E\) がすべて熱エネルギーに変換されたとする。\(E=1\text{kg}\times 9.8\text{m}/\text{s}^2\times 100\text{m}=980\text{J}\) より，\(E/(1000\text{g}\times 4.184\text{J}/(\text{g}\cdot\text{K}))\fallingdotseq 0.23\text{K}\) となって，約0.23℃温度が上昇する。

※「つい考えてしまう数学」の記事一覧はこちら