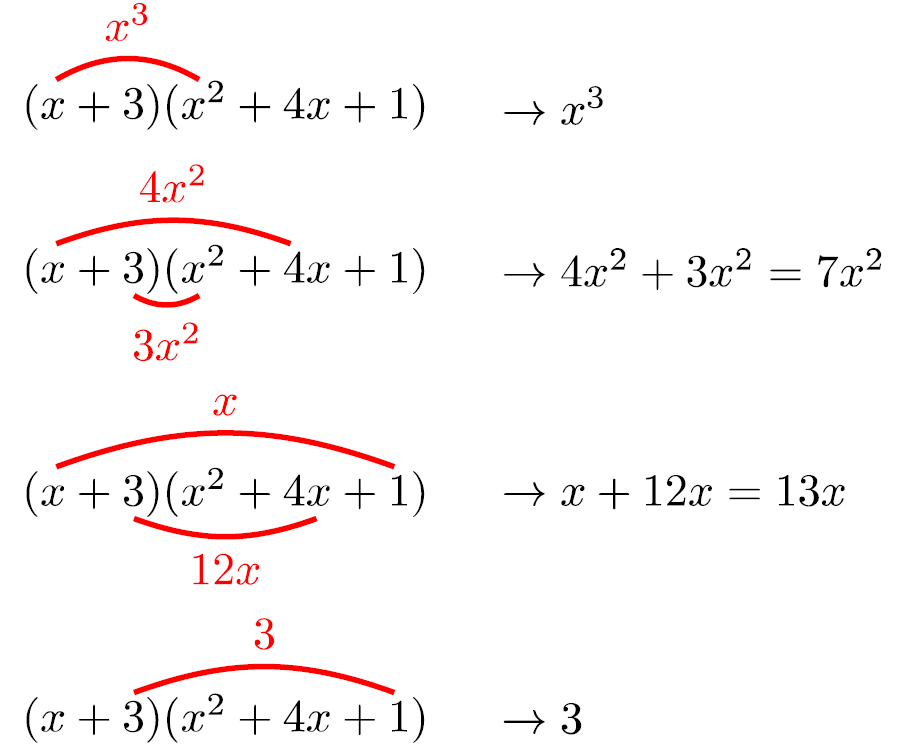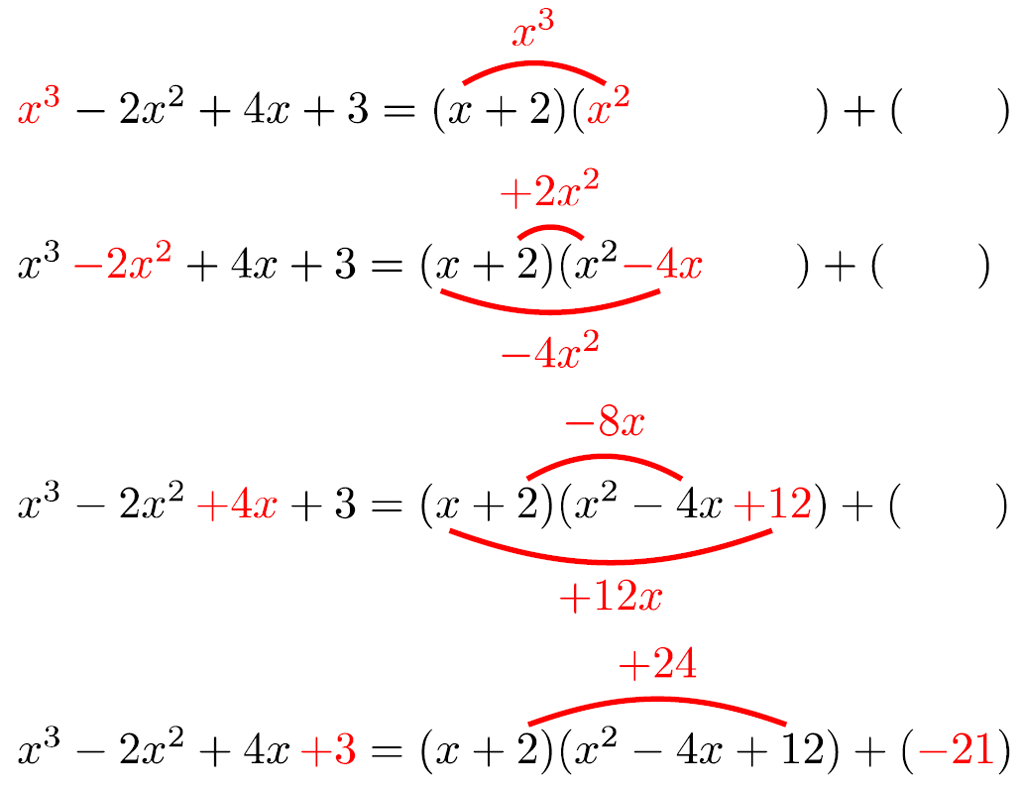特集記事（高校）

　みなさん，こんにちは。
　数学の勉強において，なんだかんだ言って，計算力は大切です!
　いくら理屈が分かって立式ができても，その後の計算ができなければ正しい結果を得られません。(1)でミスしていれば，(2)以降に大きく影響します。計算が遅い人は，再計算して確かめることもできないし，行き詰まったときに別の方法を試すこともできません。
　計算力を鍛えるには地道にコツコツと練習するしかないので，口うるさく生徒たちに言い続けましょう!

多項式の計算

　大学入試では様々な計算力が試されますが，その中でも圧倒的に触れる機会が多いのが「多項式の計算」です。ここでの計算力が色々な分野に影響します。したがって，学習初期の段階から，ある程度先を見越した指導が必要です。
　例えば，多項式の展開では，最初に仕組み（ここでは分配則）の理解の為に

という指導をすることは良いことだと思います。そして，ここから，できるだけ置き換えずに（カタマリを上手く見て）展開することを目指すというのも良いですね。特に，因数分解するときに，この「カタマリで見る」という感覚がとても大切になります。
　しかし，ここまでで終わってしまっては，結局「展開してから同類項をまとめる」という作業から抜け出せません。多項式の整理・処理がウマい人は同類項としてまとまる所を展開するのです。上記の例であれば

よって，これを整理して

\((x+3)(x^2+4x+1)=x^3+7x^2+13x+3\)

と暗算するということです。
　これを当たり前のようにできると，多項式の除法でも，筆算をせずに商と余りを求められます。例えば，\(x^3-2x^2+4x+3\) を \(x+2\) で割るときには，まず，ざっくりと

\(x^3+2x^2+4x+3=(x+2)(\color{#ff0000}{\text{2次式}}\color{#000000}{)+(}\color{#ff0000}{\text{定数}}\color{#000000}{)}\)

とイメージして，次数の高い方からツジツマをあわせていきます。

　結局のところ，展開して元に戻ることを確認しながら商と余りを求めているので，結果的に安全です。
　そして，多項式の除法に慣れたら，いわゆる次数下げをマスターしておくべきです。例えばこんな問題。

　もちろん，直接代入からの計算ゴリ押しで正解する力強さも大切ですが，やはり次数下げは必須です。（解答例はこちら）

計算力勝負の問題

　続いて，やるべきことは割と分かりやすいけど，きちんと計算をやり切れるかで勝負がつくタイプの問題を3題紹介します。
　まず1題目は，昨年ニューサポートでも紹介した九州大の空間座標の問題です。

　(2)では，面積公式

\(\triangle\text{PQR}=\dfrac{1}{2}\sqrt{\left|\overrightarrow{\text{PQ}}\right|^2\left|\overrightarrow{\text{PR}}\right|^2-\left(\overrightarrow{\text{PQ}}\cdot\overrightarrow{\text{PR}}\right)^2}\)

を使えばイイだけなので，特別な発想は不要です。しかし，実際に解いてみるとけっこうな計算力が試されます。こういう問題が合否を分けます！（解答例はこちら）

　次は，今年の京大(文系)からこの問題です。

　\(f(x)\) を \(px^2+qx+r\) とでもおいて係数比較をすれば，\(a，b，c，p，q，r\) の6文字の連立方程式になります。あとは，丁寧に文字を消去して \(a，b\) の条件に持ち込むだけなのですが，やはり差が付きやすい問題です。（解答例はこちら）

　そして最後は，文字定数が絶妙にジャマで計算力が試される積分計算です。

　計算力って大切ですね。（切実）（解答例はこちら）

　第7回は以上になります。近年の入試においては，発想力よりも計算力が要求される問題がとても多くなっています。計算の大切さを言い続けましょう！
　次回は苦手とする生徒の多い「場合の数・確率」について書く予定です。お楽しみに♪