
天理駅前広場「CoFuFun」
*写真 太田 拓実
はるかです。ここは奈良県の天理駅。駅前広場が、大きくてかっこいいね。カフェやショップもあるし、野外ステージではイベントが開かれているし、屋上トランポリンで遊んでいる子どももいるよ。にぎやか!
天理駅前広場「コフフン」だよ。デザイナーの佐藤オオキさんが設計した総合施設なんだ。モチーフは古墳なんだって。天理市には約1600基の古墳があるから、身近なシンボルなんだね。
なるほど、それでコフフン。フフン〜♩ って、ごきげんな名前だね。円盤を重ねて円錐みたいになった形もあるし、それをひっくり返したような形もあるし。立体図形としても面白い。あれ? 円錐といえば、気になっていることがあるんだった。

実は、「円錐の体積は、同じ底面と高さを持つ円柱の体積の \(\dfrac{1}{3}\)」というのが、どうもしっくり来ないんだよね。でもね、まず底面に円盤があるとして。そこに、少しずつ半径を小さくしながら、いくつもの円盤を重ねていくと考えてみたらどうかな。
へえぇ。はるかさん、おもしろいアイディアだよ。和傘を見ながら円周率について考えたときと、似た思いつきだね。
よーし! 計算してみちゃう?
えへへ。円盤を重ねたコフフンの形を見ていたら、ピンと来たんだ。例えば……そうだな。まずは、半径も高さも3mの円柱を考えてみるね。体積は
\(\pi \times 3 \times 3 \times 3=27 \pi\)(m3)
これに対して、半径が3m、2m、1mで高さがそれぞれ1mの3つの円盤を重ねたものの体積はこうなるよ。
なるほど、まずは3段階だね。
うーん。底面と高さが同じ円錐なら、体積は \(\dfrac{1}{3}\) だから
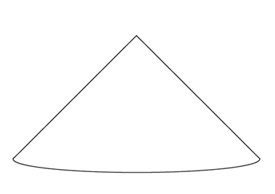
\(27 \pi \times \dfrac{1}{3}=9 \pi \)(m3)
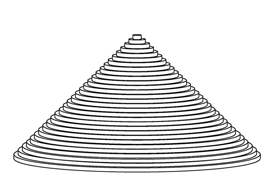
になるはずだけど、ずいぶん差が出ちゃった。もっと薄い円盤にしないと。例えば半径を10cmきざみにすれば、円盤は30個。これなら形は円錐に近づくけど……いやぁ。この計算、私にはちょっとムリだわ。
はるかさん、こんなときこそ計算ソフトだよ!
あっ、そうか。確かに、こんなときこそICTだね。計算したいのは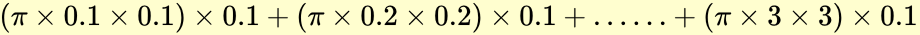
の式だから、まず\(\pi\)でくくって、かけ算の部分を計算すると
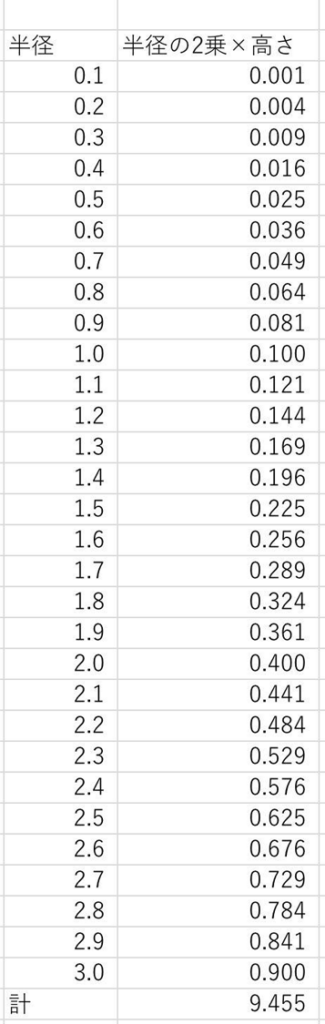
やったぁ、あっという間! 結果は9.455だよ。つまり体積は 9.455\(\pi\)m3。うん。近くなってきた。
やったね。しかもはるかさん、この方法なら、もっと細かく計算していくこともできるんじゃない?
よーし! じゃあ半径を1cmきざみにして、高さがそれぞれ1cmの円盤を300個重ねることにすると……体積は9.04505\(\pi\)m3だ。もっと行っちゃおうかな。半径を1mmきざみにして、高さがそれぞれ1mmの円盤を3000個重ねることにすると……? 体積は9.0045005\(\pi\)m3でーす!
結果の数字を並べると、おもしろい法則も見えてくるね。円錐の体積の公式は、まさにこんな考え方から導かれたんだ。
すごくすっきりしたよ、ルーロー。なんだか、とびはねたい気分。でも、コフフンの屋上トランポリンを使えるのは、小学生までだね。あははは、ちょっと残念!
*天理駅前広場「CoFuFun」/奈良県天理市。2017年オープン。古墳をイメージした野外ステージや大型遊具、カフェや観光案内所などの機能を備えている。
〒632-0016 奈良県天理市川原城町
その他のコンテンツ
