今日の授業のひと工夫(小中学校)
- TOP
- 今日の授業のひと工夫(小中学校)
- 【3年4章】走行時の速さを推測しよう②

「新編 新しい数学」3年4章p.115、116では、数学的活動を通して、ブレーキ痕の長さから自動車の走行時の速さを関数 \(y=ax^2\) を用いて推測します。ブレーキ痕の長さが自動車の速さと関係をもっていることを、生徒は何となく理解していると考えられますが、自動車の速さの2乗に比例していることは理解しづらいかもしれませんね。

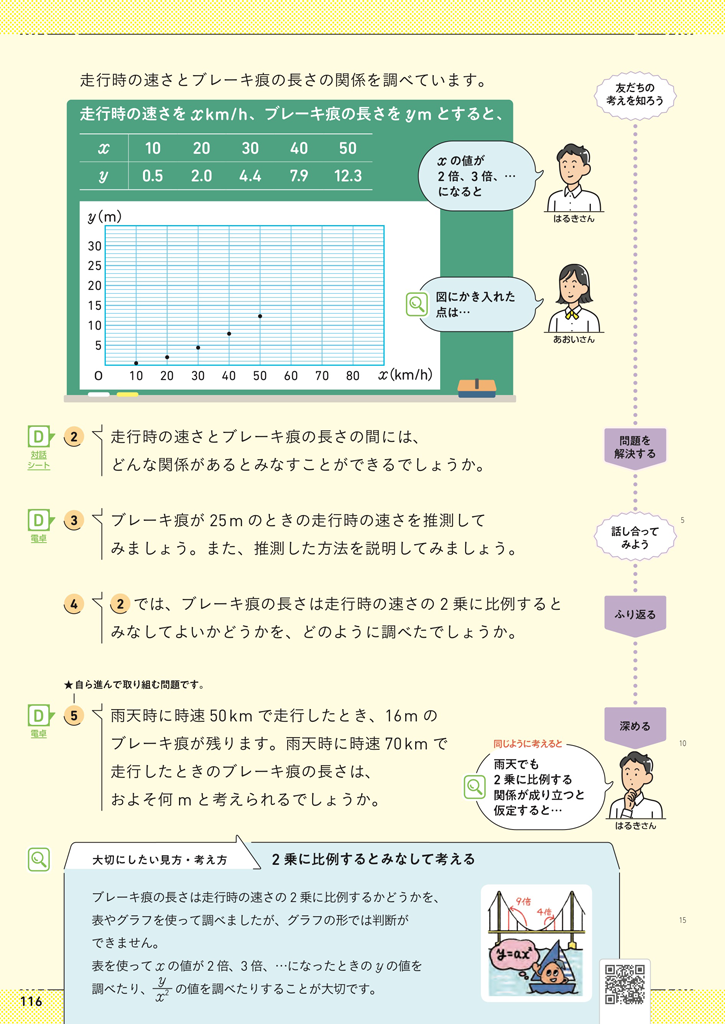
▲3年 p.115、116

②では、走行時の速さとブレーキ痕の長さの間には、どんな関係があるとみなせるのか、その根拠を聞いています。「曲線だから2乗に比例する」と説明する可能性がありますが、それはブレーキ痕の長さが速さの2乗に比例する関数であることの根拠としては不十分であることを押さえたいところです。この考えを出した生徒には、関数 \(y=ax^2\) の1つの特徴としてグラフが曲線であることに気づいた点を評価して、それに付け加えて、\(y\) の増加量がだんだん大きくなっていることや、\(x\) の値が2倍、3倍になったときの \(y\) の値の変化などの関数 \(y=ax^2\) のほかの性質や特徴を確認するとよいでしょう。
このような数学的な正しさの評価は重要です。一方で、このような現実的な事象を扱う場合では、生徒たちの推測を価値づけ、ときには素朴なもの、不十分なものも認めつつ、意見を交換するなどしながら、考えを洗練させることを大切にできるとよいですね。
関連記事はこちら
その他のコンテンツ
