特集記事（高校）

　前回，運動方程式について考えました。今回は，それを使って犯人が海に投げ捨てたはずの凶器がなぜ見つかったのかを解析します。

■物体の落下

　犯人は崖から海をみて，投げ捨てれば凶器は見つからないと考えました。下図は，前々回に提示した犯人が海を見た図です。崖の先端は崩落しそうだったので，崖の先端まではいけず，少し手前から海をみて，証拠物を海に投げ捨てて隠滅できると考えました。

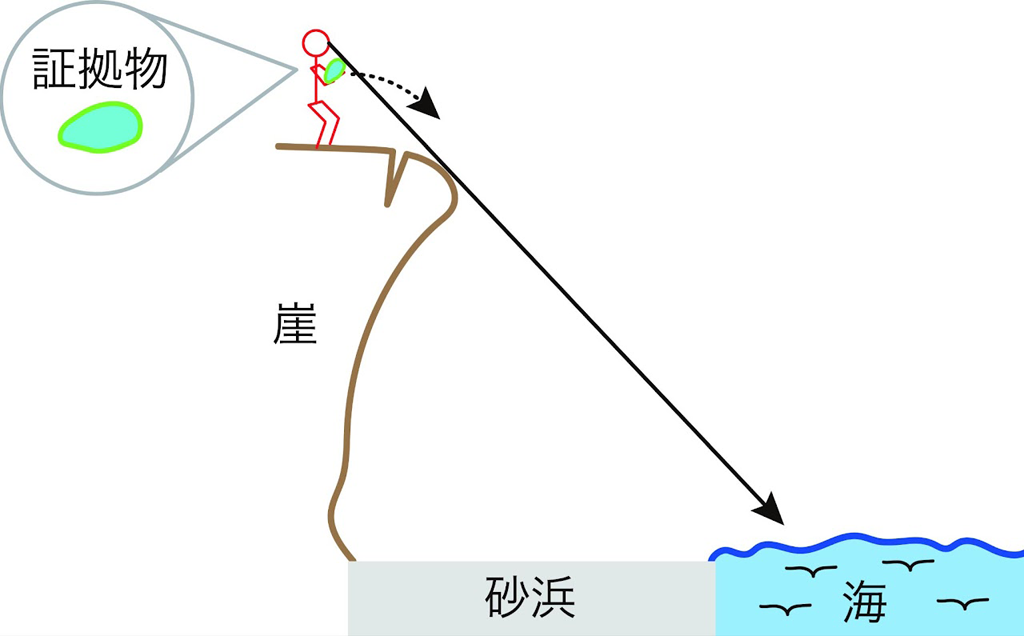
　そして，投げ捨てました。

【疑問】なぜ証拠物は見つかったのでしょうか。

　証拠物の質量を \(m\) とします。このとき，風の抵抗などはないとして，物体には（時間区間に関係なく）鉛直下向きに一定の力

\(F_{n} = (0，-mg)\)

が働いているとします。\(g\) は重力加速度（gravitational acceleration）で，値は \(g = 9.8 \text{m/s}^2\) です。\(F_n\) の第一成分の0は，\(x\) 方向には外力が働いていないという意味です。第二成分の\(-mg\) は重力で，マイナスの符号は，地表に向かう方向（リンゴが落ちた方向）を意味します。
　この \(F_n\) を速度ベクトル \(V_{n} = (v_{n}，w_{n})\) で書かれた運動方程式

\(m\cfrac{V_{n+1} – V_{n}}{\tau} = F_{n}\)

に代入し，両辺を \(m\) で割って，成分ごとに書くと次のようになります。

\(\begin{aligned} \cfrac{v_{n+1} – v_{n}}{\tau} &= 0 \\
\cfrac{w_{n+1} – w_{n}}{\tau} &= -g\end{aligned}\)

　よって， \(n = 1, 2, 3, \dots\) に対して，

\(v_n=v_1\)

\(w_{n} = w_{n-1} – g\tau = w_{n-2} – g(2\tau) = \dots = w_{1} – gt_{n-1}\)

を得ます。ここで，\(t_{n-1} = (n – 1)\tau\) です。
　さらに，

\(v_{n} = \cfrac{x_{n} – x_{n-1}}{\tau}\)

\(w_{n} = \cfrac{y_{n} – y_{n-1}}{\tau}\)

を使って，位置ベクトル \(X_{n} = (x_{n}, y_{n})\) の成分で書くと，\(x\) 成分は，

\(x_{n} = x_{n-1} + v_{1}\tau = x_{n-2} + 2v_{1}\tau = \dots = x_{0} + nv_{1}\tau = x_{0} + v_{1}t_{n}\)

となって，\(y\) 成分は，

\(\begin{aligned}y_{n} &= y_{n-1} + w_{1}\tau – gt_{n-1}\tau \\[5pt]
y_{n} &= y_{n-2} + 2w_{1}\tau – g(t_{n-2} + t_{n-1})\tau \\[5pt]
y_{n} &= y_{n-3} + 3w_{1}\tau – g(t_{n-3} + t_{n-2} + t_{n-1})\tau \\[5pt]
&\phantom{y_n} \vdots \phantom{y_{n-1} + w_{1}\tau} \\[5pt]
y_{n} &= y_{0} + nw_{1}\tau – g(t_{0} + \dots + t_{n-3}+ t_{n-2} + t_{n-1})\tau \end{aligned}\)

となります。ここで，

\(\begin{aligned}(t_{0} + t_{1} + \dots + t_{n-2} + t_{n-1})\tau &= (0 + 1 + \dots + (n-2) + (n-1))\tau^2 \\[5pt] &= \cfrac{n\tau(n-1)\tau}{2} = \cfrac{t_{n}(t_{n} – \tau)}{2} \end{aligned}\)

と \(t_{n} = n\tau\) を使うと，

\(y_{n} = y_{0} + w_{1}t_{n} – \cfrac{gt_{n}(t_{n} – \tau)}{2} = y_{0} + ({\color{#ff0000}w_{1} + \cfrac{g\tau}{2}})t_{n} – \cfrac{gt_{n}^2}{2}\)

を得ます。\(y\) 方向の初速度を \(\color{#ff0000}w_{1} = -\cfrac{g\tau}{2}\) とできたと仮定すると，

\(\begin{aligned}x_{n} &= x_{0} + v_{1}t_{n} \\[5pt]
y_{n} &= y_{0} – \frac{gt_{n}^2}{2} \end{aligned}\)

となります。
　時間間隔 \(\tau\) が小さければ，\(y\) 方向の初速度 \(w_1\) も非常に小さいので，水平方向から少しだけ下に向かう方向が初速度ベクトルになります。\(t_n\) を \(t\) に置き換えて，\(x_n\)，\(y_n\) をそれぞれ \(x(t)\)，\(y(t)\) のように \(t\) の関数にします。

\(\begin{aligned}x(t) &= x_{0} + v_{1}t \\[5pt]
y(t) &= y_{0} – \cfrac{gt^2}{2}\end{aligned}\)

　こうすれば，\(t=t_n\) のときの物体の位置は \((x(t)，y(t))=(x_n，y_n)\) となり，さらに，\(t_n\) と \(t_{n+1}\) の間の時間の位置についても補間できます。

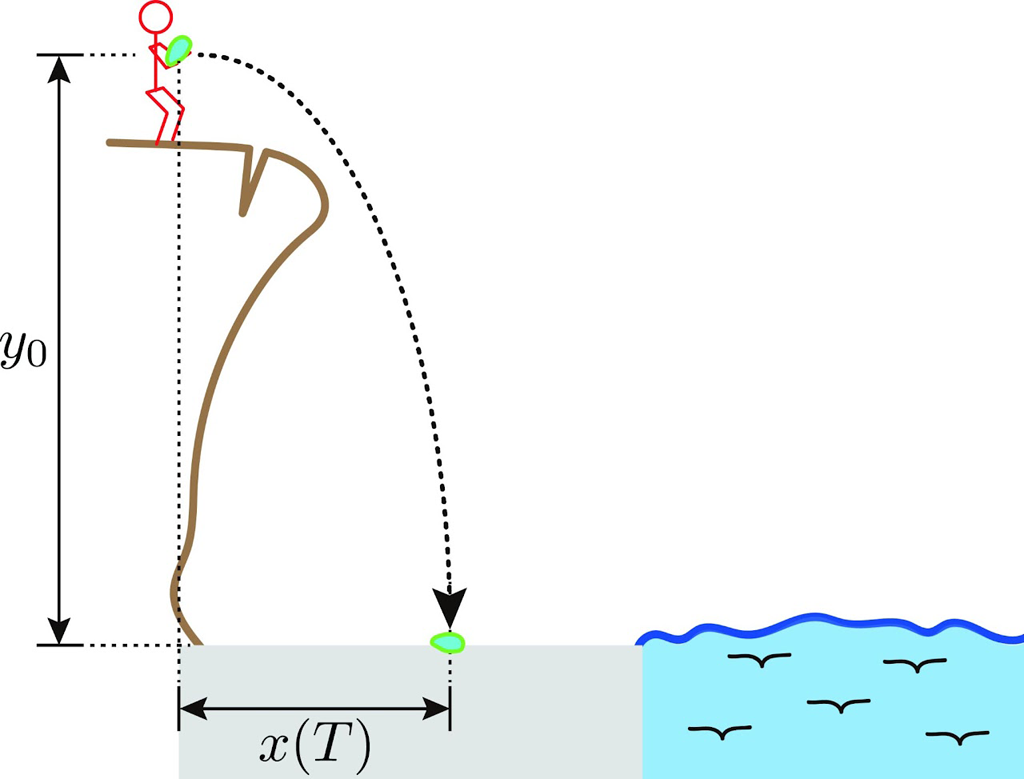
　海の表面と砂浜の高さを0とし，犯人が証拠物を投げ捨てた高さを \(y_0\) とします。\(x\) 方向（水平方向）の初期位置と初速度をそれぞれ \(x_0=0\) と \(v_1\gt0\) とすると，証拠物は，水平方向（ \(x\) 方向）に等速運動し，鉛直下向き方向（ \(-y\) 方向）に時間の2乗に比例した距離を落下します。そして，ある時刻 \(T\) で \(y(T)=0\) となります。実際，

\(T = \sqrt{\cfrac{2y_{0}}{g}}\)

です。
　いよいよ【疑問】に答える準備ができました。

【解答例】

　例えば，\(y_0=10\text{m}\) とします。重力加速度は \(g = 9.8\text{m/s}^2\) なので，\(T = 1.43\text{s}\) となります。水平方向の初速度を \(v_{1} = 2\text{m/s}\)（かなりの早歩き）とすると，\(x(T) = 2.86\text{m}\) になります。砂浜部分は崖から5m以上だったので，落下距離がたかだか3mでは海に投げ入れられず，犯人は証拠隠滅に失敗しました。

■容疑者の確保

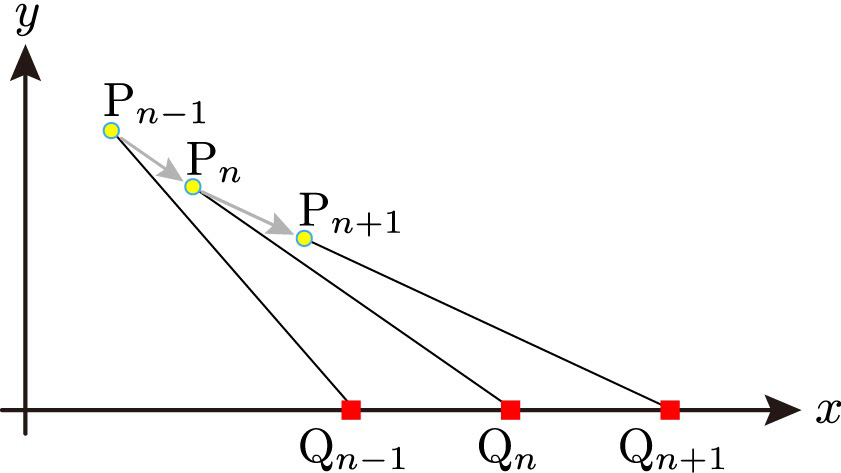
　容疑者は \(x\) 軸上を正の方向に一定の速度 \(v_s\gt0\) で歩いている。\(s\) は容疑者（suspect）の頭文字。時刻 \(t_n\) における容疑者の位置を点 \(Q_n(q_n，0)\) とする。\(q_0=0\) とすると，\(q_n=v_st_n\) である。
　容疑者を追跡する刑事の時刻 \(t_n\) における位置を点 \(P_n(x_n，y_n)\) とする。刑事は一定の速さ \(v_l \gt0\) を保ちつつ容疑者に近づいて確保しようとしている。\(l\) は警部補（lieutenant）の頭文字。

　刑事は尾行の回の話と同様な追跡方法をとります。

【追跡方法】

　刑事は容疑者が一定の速度で移動していることに気が付いているので，時刻 \(t_{n-1}\) で点 \(P_{n-1}\) にいた刑事は，次の時刻 \(t_n\) に容疑者が点 \(Q_n\) に移動することが予測できる。時刻 \(t_n\) において刑事は点 \(P_{n-1}\) から点 \(Q_n\) 方向に \(\tau\) 時間進んだ点 \(P_n\) に移動する。
　容疑者と刑事の距離は徐々に縮まり，つねに \(P_{n-1}P_{n} = v_{l}\tau\) を満たしています。これより，

\(\begin{aligned}\overrightarrow{P_{n-1}P_{n}} &= v_{l}\tau \cfrac{\overrightarrow{P_{n-1}Q_{n}}}{d_{n}} \\[5pt]
d_{n} &= P_{n-1}Q_{n}\end{aligned}\)

がわかります。成分表示すると，

\(\begin{aligned}x_{n} – x_{n-1} &= (q_{n} – x_{n-1})\cfrac{v_{l}\tau}{d_{n}} \\[5pt]
y_{n} – y_{n-1} &= -y_{n-1}\cfrac{v_{l}\tau}{d_{n}} \\[5pt]
d_{n} &= \sqrt{(q_{n} – x_{n-1})^2 + y_{n-1}^2} \\[5pt]
q_{n} &= v_{s}t_{n}\end{aligned}\)

となります。あとはこれを解けばよいです。

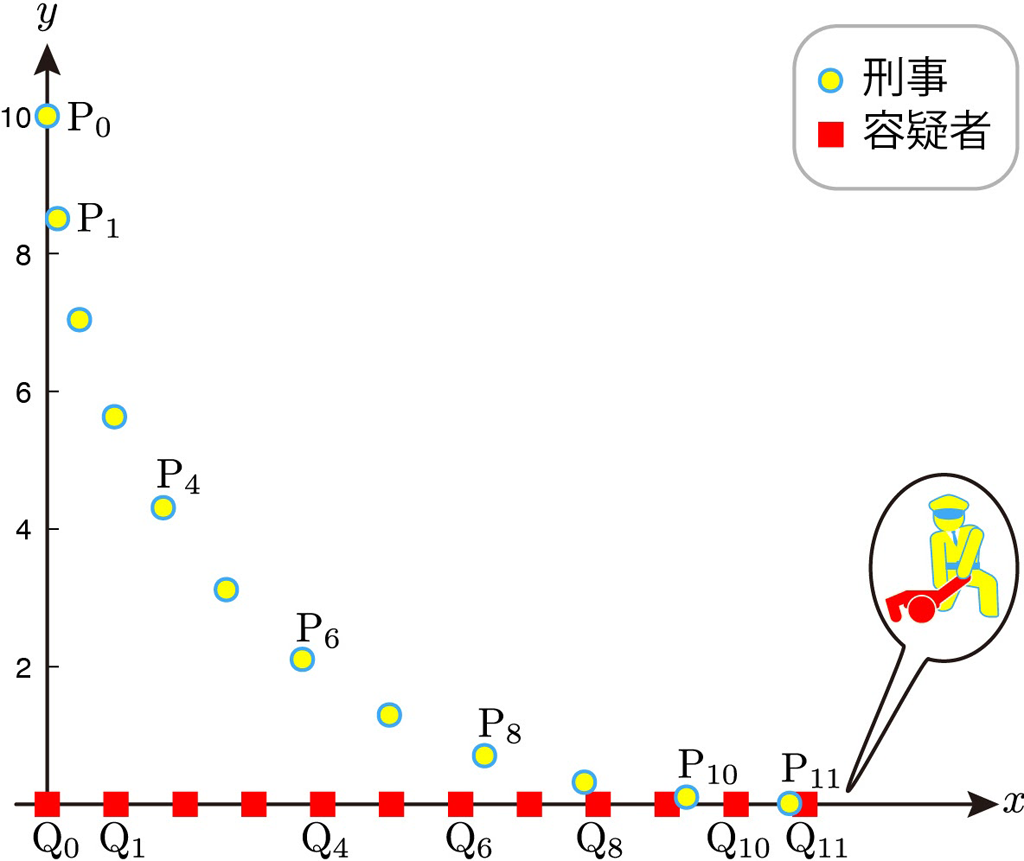
【確保例】

　上の図は以下のようなサンプルデータにもとづいて \(n = 1, 2, \dots,11\) まで順次計算して描いた図です。

• 刑事の初期位置 \(P_{0}(x_{0}， y_{0}) \) を \(x_0=0\text{m}\)，\(y_0=10\text{m}\)（つまり， \(y\) 軸上の点）
• 容疑者の初期位置 \(Q_0\) を原点（ \(q_0=0\text{m}\) ）
• 刑事の歩行速度は早歩き程度の \(v_l=1.5\text{m/s}\)
• 容疑者の歩行速度は \(v_{s} = 1\text{m/s}\)
• 時間間隔は \(\tau=1\text{s}\)

　このデータによると，刑事と容疑者の距離は，\(10\text{s}\) で \(0.7\text{m}\)，\(11\text{s}\) で \(0.2\text{m}\) なので，だいたい11秒で確保にいたりました。

　これにて，一件落着！

■ライプニッツの贈り物

　容疑者の尾行（尾行の回の話）や確保した軌跡は，一般にトラクトリックス（tractrix），牽引線，追跡線，犬曲線（hundkurve［独］）などと呼ばれる曲線に近い。MacTutorによれば，1692年にホイヘンスが初めて研究し，彼がtractrixと名付けた。その後，ライプニッツ，ヨハン・ベルヌーイなどがこの曲線を研究した。特に，ライプニッツが次の問題を提出したことから始まった。
『一定の長さの弦で水平面に沿って引っ張られる物体の軌跡は，物体に接続されていない側の弦の端が平面内で直線に沿って動くときどうなるか』

　ライプニッツは，軸がトラクトリックスの漸近線であるという事実を利用してこれを解決したようである。物体を犬，弦をリードとし，犬の飼い主が（動きたくない）犬を水平方向に引っ張るさまに近いので，この曲線はドイツ語で hundkurve（犬曲線）とも呼ばれる。
　ライプニッツ（Gottfried Wilhelm von Leibniz, 1646－1716［独］）は，ニュートンとともに微積分学を創始したドイツの数学者，哲学者である。微分の記号 \(dx\)，\(dy\) や，微分商 \(\cfrac{dy}{dx}\) ，あるいは不定積分の記号 \(\int f(x)dx\) はいずれもライプニッツによる。ヨハンは，兄のヤコブ（かつヨハンの指導教官）と共に，ライプニッツの微積分法の（熱心な？）支持者であった。

注　定積分 \(\int_a^b f(x) dx\) はフーリエ，導関数 \(f'(x)\) はラグランジュによる。

※「つい考えてしまう数学」の記事一覧はこちら