
前回,犯人は容疑者として特定され,刑事に尾行されました。そもそも容疑者になった理由は凶器が発見されたからです。海に投げ捨てられたはずの凶器はなぜ見つかったのでしょうか。それを解析するために,今回は運動方程式について考えます。少し話が逸れますが,車は急に止まれないことを,運動方程式を用いて理解します。
【疑問】なぜ「車は急に止まれない」といわれるのでしょうか。
【速度ベクトルと加速度ベクトル】
\(xy\) 座標平面上を動く点(動点)の位置を一定の時間間隔 \(\tau \gt 0\) で記録します。記録した時刻を \(t_n=n\tau\) とし,そのときの動点の座標を \((x_n,y_n)\) としましょう。初期時刻は \(t_0=0\) で,初期位置は \((x_0,y_0)\) です。以降,\(n\) は,\(n=1,2,3\) …と増えていきます。
動点の \(x\) 座標の時間変化だけに着目しましょう。
時刻 \(t_n\) と動点の \(x\) 座標 \(x_n\) の組 \((t_n,x_n)\) を \(tx\) 座標平面上の点の座標としてプロットし,点 \((t_n,x_n)\) 付近を拡大すると下図のようになります。この図は前回もみました。
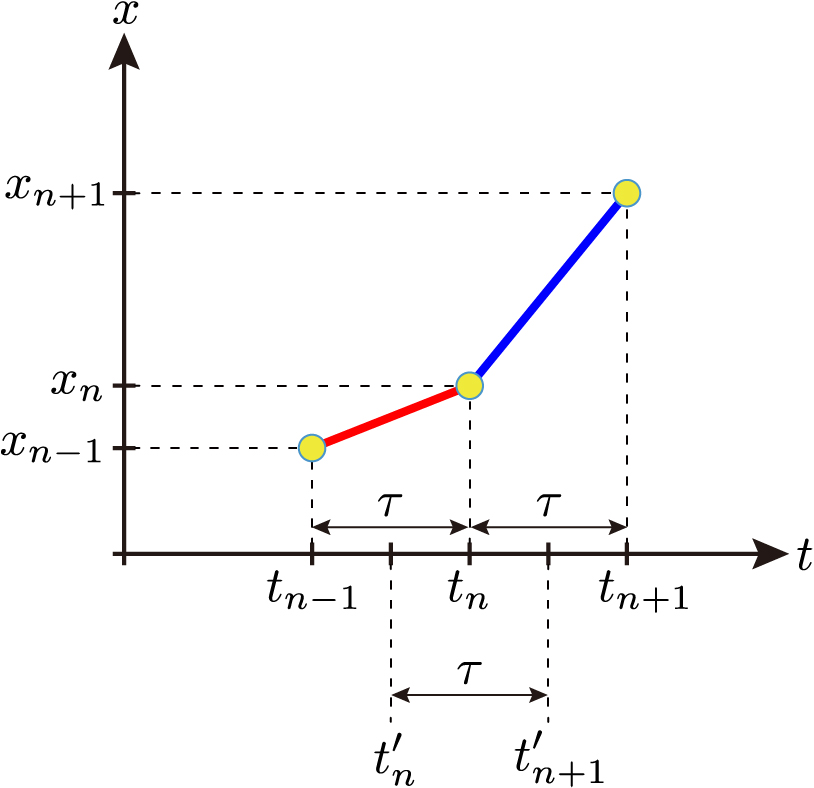
時間区間 \([t_{n-1},t_n]\) の中点を \(t_n’\) とし,時刻 \(t_n’\) における瞬間の速度を時間区間 \([t_{n-1},t_n]\) における位置の変化率 \(v_n\) で定義しました。\(v\) は速度(velocity)の頭文字です。
\(v_n=\cfrac{x_n-x_{n-1}}{\tau}(n=1,2,3,\cdot\cdot\cdot)\)
これは上の図における赤い線分の傾きです。\(v_{n+1}\) は青い線分の傾きで,\(t_{n+1}’\) における瞬間の速度となります。
時刻 \(t_n\) での速度は(使わないので)定義しませんが,その代わり時刻 \(t_n\) での速度の変化率を考えましょう。
時間区間 \([t_n’,t_{n+1}’]\) における速度の変化率を
\(a_n=\cfrac{v_{n+1}-v_n}{\tau}\)
と書いて,これを平均加速度と呼ぶことにします。\(a\) は加速度(acceleration)の頭文字です。時刻 \(t_n’\) の瞬間の速度を \(v_n\) とみなしたように,時間区間 \([t_n’,t_{n+1}’]\) の中点は \(t_n\) であるから,\(a_n\) を時刻 \(t_n\) の瞬間の加速度と定義します。
加速度を位置の座標を用いて表現すると,
\(a_n=\cfrac{x_{n+1}-2x_n+x_{n-1}}{\tau^2}\)
となることから,\(a_n\) の実体は,時間幅 \(2\tau\) の時間区間 \([t_{n-1},t_{n+1}]\) における平均加速度といえます。
動点の \(y\) 座標の時間変化だけに着目しても,同じことがいえます。
例えば,下図は,\(y\) 軸が鉛直上向きであるとして,鉛直下向きに落下するリンゴで,動点はその重心です。
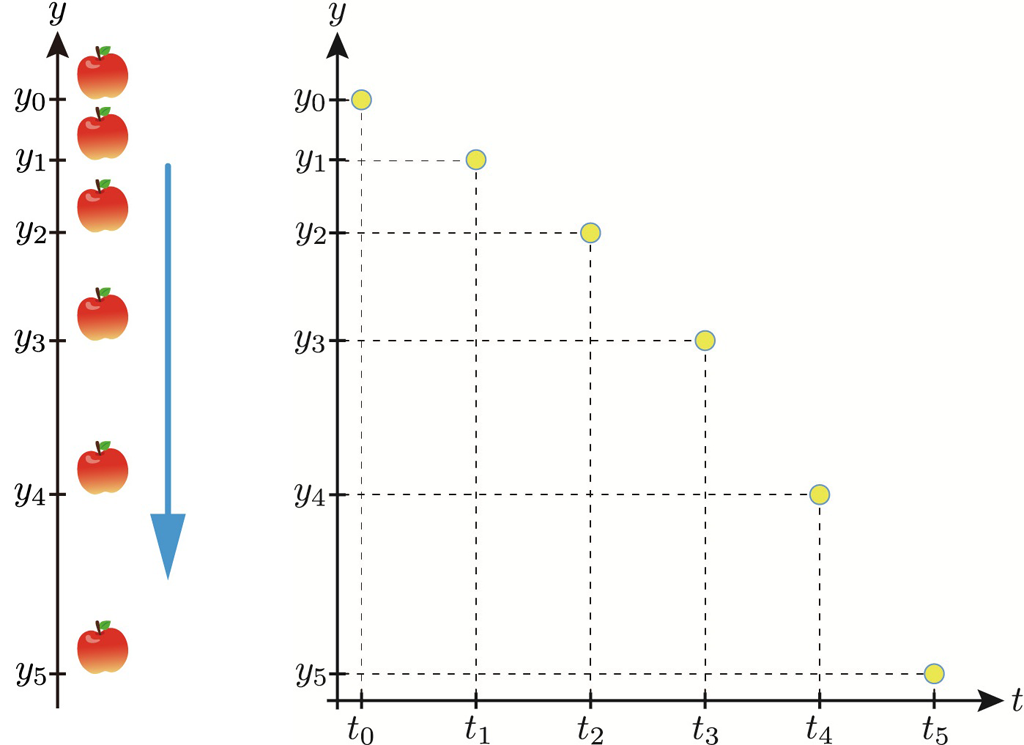
上の図(左)は,\(y\) 軸に沿って落下するリンゴの下端の位置 \(y_n\) を時刻 \(t_n\) ごとに記録した図です。図(右)は,点 \((t_n,y_n)\) を \(ty\) 座標平面上の点の座標としてプロットした図です。
この場合も \(x\) 軸上の動点の運動と同様に,時刻 \(t_n’\) における速度と時刻 \(t_n\) における加速度をそれぞれ
\(w_n=\cfrac{y_n-y_{n-1}}{\tau}\)
\(b_n=\cfrac{w_{n+1}-w_n}{\tau}=\cfrac{y_{n+1}-2y_n+y_{n-1}}{\tau^2}\)
と定義できます。アルファベットで,\(v\) の次は \(w,a\) の次は \(b\) なので,速度と加速度の文字をそれぞれ \(w,b\) にしました。
下の図は,\(xy\) 平面内で放り投げられたボールを時刻 \(t_n\) ごとに記録した図です。時刻 \(t_n\) におけるボールの重心の位置を点 \(\text{P}_n(x_n,y_n)\) とします。点 \(\text{P}_n(x_n,y_n)\) の位置ベクトルを,
\(\boldsymbol{X}_n=(x_n,y_n)\)
と太文字で書きましょう。\(x_n\) と書くと,第一成分 \(x_n\) と紛らわしいので,大文字で \(\boldsymbol{X}_n\) としました。
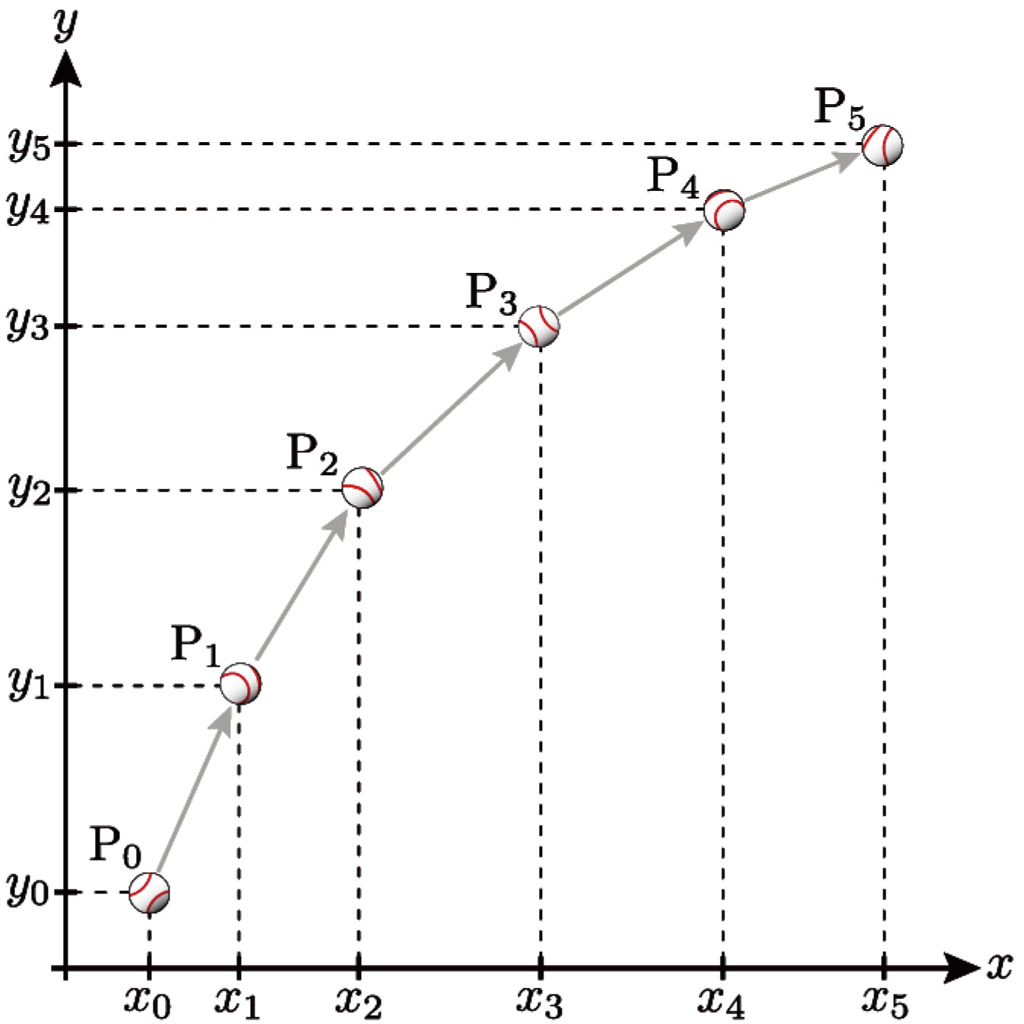
再び,時間区間 \([t_{n-1},t_n]\) の中点を \(t_n’\) としましょう。時間区間 \([t_{n-1},t_n]\) における位置ベクトルの変化率を平均速度ベクトルと呼び,それを時刻 \(t_n’\) における速度ベクトルと定義して,
\(\boldsymbol{V}_n=\cfrac{X_n-X_{n-1}}{\tau}\)
と表します。速度ベクトル \(\boldsymbol{V}_n\) の成分を \(\boldsymbol{V}_n=(v_n,w_n)\) とすると
\(v_n=\cfrac{x_n-x_{n-1}}{\tau}\),\(w_n=\cfrac{y_n-y_{n-1}}{\tau}\)
となります。\(v_n\) と書くと,第一成分 \(v_n\) と紛らわしいので,大文字で \(\boldsymbol{V}_n\) としました。
同様に,時刻 \(t_n\) における加速度ベクトルも
\(\boldsymbol{A}_n=\cfrac{\boldsymbol{V}_{n+1}-\boldsymbol{V}_n}{\tau}\)
のように定義します。加速度ベクトル \(\boldsymbol{A}_n\) の成分を \(\boldsymbol{A}_n=(a_n,b_n)\) とすると,
\(\begin{alignedat}{2}a_n &=\cfrac{v_{n+1}-v_n}{\tau}&&=\cfrac{x_{n+1}-2x_n+x_{n-1}}{\tau^2} \\
b_n &=\cfrac{w_{n+1}-w_n}{\tau}&&=\cfrac{y_{n+1}-2y_n+y_{n-1}}{\tau^2}\end{alignedat}\)
となります。\(a_n\) と書くと,第一成分 \(a_n\) と紛らわしいので,大文字で \(\boldsymbol{A}_n\) としました。
【運動量と力】
以上の準備のもと,ニュートンの運動方程式を導出しましょう。まず,運動量という量を定義します。そのために次の二つの極端な状況を想像してください。
A:大型トラックが猛スピードで走っている。
B:軽自動車がのろのろと走っている。
あるいは
A:運動会の大玉転がしの大玉が鉄球で,それが猛スピードで転がってきた。
B:ピンポン球がゆっくり転がってきた。
いずれの場合も Aの方が脅威を感じ,Bの方は恐ろしいとは思いませんね。
このように,重くて速い物体と軽くて遅い物体は,明らかに運動の激しさが異なります。この激しさを量的に表したものを物体の運動量といって,質量と速度の積で定義します。速度がベクトルの場合,運動量もベクトルになります。
運動量 = 質量 × 速度
(運動量ベクトル = 質量 × 速度ベクトル)
ここで,質量(慣性質量)とは,止まっているものの動きにくさ,動いているものの止まりにくさ,あるいは速度変化のしにくさを表す量です。
\(xy\) 座標平面上の質量 \(m\) の物体の時刻 \(t_n\) における位置の座標を \((x_n,y_n)\) とし,時刻 \(t_n\) の速度ベクトルを \(V_n\) とします。\(m\) は質量(mass)の頭文字です。このとき,時刻 \(t_n\) の運動量ベクトルを \(\boldsymbol{p}_n\) とすると,
\(\boldsymbol{p}_n=mV_n\)
となります。
時刻 \(t_n’\) から \(\tau\) 時間経った \(t_{n+1}’\) の間に,運動量が \(\boldsymbol{p}_n\) から \(\boldsymbol{p}_{n+1}\) に変化したとします。このとき,その変化には原因があったと考えて,その原因を力(force)と呼びます。
時間区間 \([t_n’,t_{n+1}’]\) において一定方向に一定の大きさの力 \(\boldsymbol{F}_n\) が働いた場合,
\(\boldsymbol{p}_{n+1}-\boldsymbol{p}_n=\boldsymbol{F}_n\tau\)
のように表現します。\(\boldsymbol{p}_n\) はベクトルなので,\(\boldsymbol{F}_n\) もベクトルです。右辺は力積と呼ばれます。
【ニュートンの運動方程式】
運動量の \(\tau\) 時間の変化率は
\(\cfrac{\boldsymbol{p}_{n+1}-\boldsymbol{p}_n}{\tau}=\boldsymbol{F}_n\)
であるので,力 \(\boldsymbol{F}_n\) によって,運動量の変化の割合と変化の方向が定まります。この式をニュートンの運動方程式,あるいは単に運動方程式と呼びます。
運動方程式に \(\boldsymbol{p}_n=m\boldsymbol{V}_n\) を代入すると
\(\cfrac{m(\boldsymbol{V}_{n+1}-\boldsymbol{V}_n)}{\tau}=\boldsymbol{F}_n\)
より,加速度ベクトル \(\boldsymbol{A}_n\) を用いて,時刻 \(t_n\) における運動方程式が
\(m\boldsymbol{A}_n=\boldsymbol{F}_n\)
となります。この式は,質量 \(m\) の物体に力 \(\boldsymbol{F}_n\) が加えられたとき,結果として,この物体に加速度 \(\boldsymbol{A}_n\) が生じる,という因果関係を表す式です。あるいは,物体に加速度があるのならば,その物体には,その加速度ベクトルと同じ方向に,大きさが \(m\) 倍された力が働いていると言い換えられます。
位置ベクトルを用いて書けば,
\(\cfrac{m(\boldsymbol{X}_{n+1}-2\boldsymbol{X}_n+\boldsymbol{X}_{n-1})}{\tau^2}=\boldsymbol{F}_n\)
となります。運動量の変化率を \(\boldsymbol{p}\),\(\boldsymbol{V}\),\(\boldsymbol{A}\),\(\boldsymbol{X}\) を用いてさまざまに表現しましたが,いずれの方程式も運動方程式と呼びます。スカラー量の場合は,
\(ma_n=\cfrac{m(v_{n+1}-v_n)}{\tau}=\cfrac{m(x_{n+1}-2x_n+x_{n-1})}{\tau^2}=f_n\)
となります。
運動している質量 \(m\) の物体の動きは,その物体に働くであろうさまざまな力 \(\boldsymbol{F}_n\) (スカラーなら \(f_n\) )を与えて,運動方程式を解いて求めます。
(後半では,いよいよ車は急に止まれないことを運動方程式を用いて考えます。)
※「つい考えてしまう数学」の記事一覧はこちら
1970年東京生まれ。早稲田大学理工学部数学科卒業。東京大学大学院数理科学研究科数理科学専攻博士課程修了。現在,明治大学理工学部数学科専任教授。博士(数理科学)。専門は応用数理,特に界面現象の数理解析。実験を採り入れた数学の講義で定評がある。
| 著書: | 『実験数学読本』①・②・③ (日本評論社),『次元解析入門』,『界面現象と曲線の微積分』,『動く曲線の数値計算』(以上共立出版),『大学数学の教則』(ちくま学芸文庫),『公式は覚えないといけないの?』(ちくまプリマー新書),他。 |
その他のコンテンツ
