特集記事（高校）

（前編はこちら）

　最初の【疑問】戻りましょう。なぜ「車は急に止まれない」といわれるのでしょうか。

【車は急に止まれない】

　一直線（\(x\) 軸）上を質量 \(m\) の車が一定速度 \(v_0 \gt 0\) で走っているとします。いま，ブレーキを踏んで，緊急停止しなければならなくなりました。ブレーキを踏もうと思ってから，実際に車が停止するまでの距離に \(v_0\) がどのように依存しているのかを調べます。以下のように二つの過程に分けて考えます。

• 過程１

　ブレーキを踏もうと思い立ってから，実際にブレーキが効き始めるまでの過程。かかった時間を反応時間 \(T_r\)（reaction time）とし，その間に車が移動した距離を空走距離 \(D_r\)（reaction distance, thinking distance）とする。

• 過程2

　ブレーキが効き始めてから車が完全に停止するまで，すなわち速度が0になるまでの過程。かかった時間を制動時間 \(T_b\)（braking time）とし，その間に車が移動した距離を制動距離 \(D_b\)（braking distance）とする。

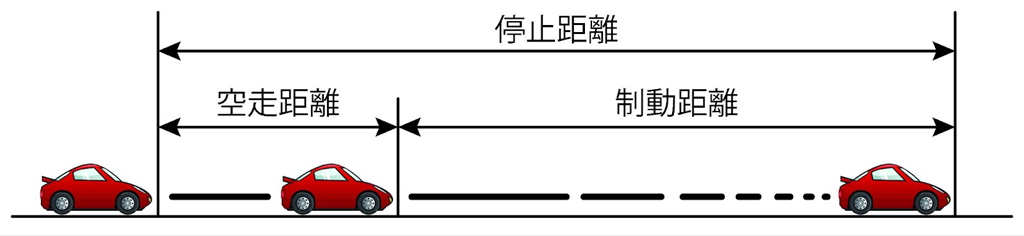
　空走距離と制動距離を合わせた距離を停止距離（stopping distance）と呼びます。下図は停止距離のイメージ図です。

　下図はあるサンプルデータの速度 \(v_0\) と停止距離 \(D_r+D_b\) の関係を表した棒グラフです。

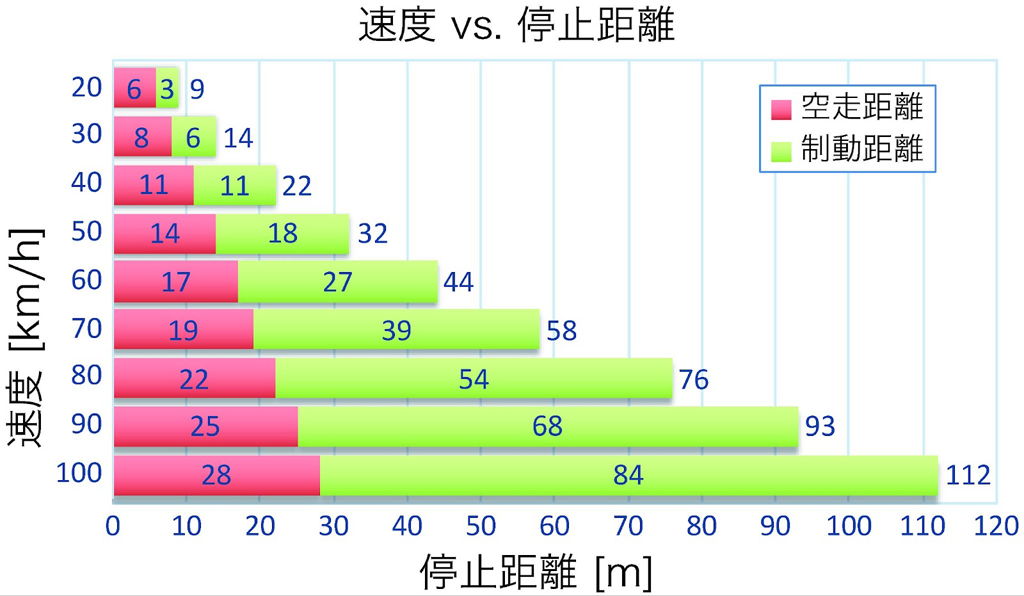
　この棒グラフからわかることは，目安として時速100kmならば車が停止するまで100m以上の距離が必要で，時速80km，90kmならば，停止距離はおよそ80m，90mであることです。高速道路で車間距離の目安にする0m（確認基点），50m，100mの表示がありますが，時速80kmで走行していたら，80m以上は車間距離を空けておくと，いざというときに安全ということがわかります。

　この棒グラフは『空走時間を1秒とし，乾燥した舗装路面で急ブレーキをかけた場合の最短の停止距離』における実験データをもとにしています。（トヨタ中央自動車学校，連載コラム『車は急には止まれない』に掲載されていた停止距離のデータ。現在この連載はなくなってリンク切れ。）

　路面が濡れていたり，急ブレーキをかけなかったりすると，制動距離はもっと大きくなるので，時速80kmなら車間距離は80mという数値は最低限の指標と認識しておくとよいでしょう。

※神奈川県警察の高速安全走行のポイント「高速道路安全運転5則」の「2　十分な車間距離を取る」では，雨の日の車間距離は約2倍と注意喚起しています。

【制動時間】

　車のブレーキで直接制御できるのは，ブレーキを踏んだときの車の速度ではなく，車にかかる力です。上述した運動方程式からわかるように，力を通して加速度，つまり速度の変化率を制御することができるのです。

　\(x\) 軸上の正の方向に質量 \(m\) の車が一定速度 \(v_0 \gt 0\) で走っているとします。
　まず，空走距離は \(D_r=v_0T_r\) です。
　次に，制動距離 \(D_b\) を求めましょう。そのために，制動時間 \(T_b\) を求めます。ブレーキが効き始めた時刻を \(0\) とし，制動時間 \(T_b\) の間，車の進行方向と逆向きにある一定の力 \(f \gt 0\) が働き続け，時刻 \(T_b\) で車が完全に停止したとします。
　車の外部にいる観測者が一定時間間隔 \(\tau\) おきに車の位置を計測していて，

\(t_n=n\tau(n=0,1,2,\cdot \cdot \cdot)\)，\(t_{N-1} \lt T_b\leqq t_N\)

であったとします。

※ \(t_{N-1}\lt T_b \leqq t_N\) のときは，\(N-1\) 回目と \(N\) 回目の計測の間で車が停止したときで，\(T_b=t_N\) のときは，ちょうど \(N\) 回目の計測で車が停止したときです。

　\(x_n\) を時刻 \(t_n\) における車の位置とします。計測しているのは位置のみです。時間区間 \([t_{n-1}，t_n]\) における平均速度を \(v_n=\cfrac{x_n-x_{n-1}}{\tau}\) とし，これをこの時間区間の真ん中の時刻 \(t_n’=\cfrac{t_{n-1}+t_n}{2}\) における瞬間の速度とします。これは上述してきた設定と同じです。

　仮定から時刻 \(t’_0 \lt 0\) ときの速度は一定速度 \(v_0\) で，時刻 \(t_{N+1}\) のときの速度は，停止後だから \(v_{N+1}=0\) とします。

　次に，時刻 \(t_n\) を含む時間幅 \(\tau\) の時間区間 \([t’_n，t’_{n+1}]\) における運動量の変化率は，\(\tau\) 時間に作用した力に等しく，その力は，車の進行方向に対して \(-f\lt 0\) でした。運動方程式を立てると，

\(\cfrac{mv_{n+1}-mv_n}{\tau}=-f(n=0,1,2,\cdot \cdot \cdot,N)\)

です。\(n=0,1,2,\cdot \cdot\cdot,N\) から順に書き並べると以下の \(N+1\) 個の連立方程式になります。

\(\cfrac{mv_1-mv_0}{\tau}=-f\)

\(\cfrac{mv_2-mv_1}{\tau}=-f\)

…

\(\cfrac{mv_{N+1}-mv_N}{\tau}=-f\)

　よって，これらすべてを辺々足し合わせると，\(v_{N+1}=0\) なので，

\(\cfrac{-mv_0}{\tau}=-(N+1)f\)

を得ます。\(t_N=N\tau\) なので，両辺に \(\tau\) をかけて，両辺を \(f\) で割り，次式を得ます。

\(\cfrac{mv_0}{f}=t_N+\tau\)　⇔　\(t_N=\cfrac{mv_0}{f}-\tau\)

　制動時間 \(T_b\) は，\(t_{N-1}=t_N-\tau \lt T_b \leqq t_N\) の範囲だったので，

\(\cfrac{mv_0}{f}-2\tau \lt T_b \leqq\cfrac{mv_0}{f}-\tau\)

がわかります。
　よって，\(\tau\) が非常に小さかったら，

\(T_b \fallingdotseq \cfrac{mv_0}{f}\)

と見なせるので，制動時間は，速度に比例することがわかります。だから車は急に止まれないのです。

【制動距離】

　次に制動距離 \(D_b\) を求めましょう。各 \(k=1,2,\cdot \cdot \cdot,N\) に対して，\(k\) 個の運動方程式

\(\cfrac{mv_1-mv_0}{\tau}=-f\)

\(\cfrac{mv_2-mv_1}{\tau}=-f\)

…

\(\cfrac{mv_k-mv_{k-1}}{\tau}=-f\)

の辺々をすべて足して，式変形すると，

\(v_k=v_0-\cfrac{f}{m}t_k(k=1,2,\cdot \cdot \cdot,N)\)

となります。\(v_k=\cfrac{x_k-x_{k-1}}{\tau}\) だったので，

\(x_k-x_{k-1}=v_0\tau-\cfrac{f}{m}t_k\tau(k=1,2,\cdot \cdot \cdot,N)\)

を得ます。この両辺を \(k=1,2,\cdot \cdot \cdot,N\) について和をとると，

\(x_N-x_0=v_0t_N-\cfrac{f}{m}\displaystyle \sum_{k=1}^N t_k\tau\)

となりますが，左辺は制動距離 \(D_b\) に他なりません。右辺の和 \(\sum\) の部分は，次のように変形できます。

\(\displaystyle \sum_{k=1}^Nt_k=\displaystyle \sum_{k=1}^Nk\tau=\cfrac{N(N+1)}{2}\tau=t_N\cfrac{N+1}{2}\)

これに \(\tau\) をかけて，上で計算した \(t_N+\tau=\cfrac{mv_0}{f}\) を代入すると，

\( \begin{aligned}D_b & =x_N-x_0=v_0t_N-\cfrac{f}{m}t_N\cfrac{t_N+\tau}{2} \\ & =\cfrac{v_0t_N}{2}=\cfrac{v_0(\cfrac{mv_0}{f}-\tau)}{2} \fallingdotseq \cfrac{{mv_0}^2}{2f}\end{aligned}\)

となることがわかります。つまり，制動距離は速度の2乗に比例する，といえます。例えば，時速50kmから時速100kmに速度をあげた場合，制動距離は4倍に増えます。

※ 上述した棒グラフのデータでは，18mから84mなので，4.7倍です。

※ \(T_b \fallingdotseq \cfrac{mv_0}{f}\) であったことを使えば，\(D_b \fallingdotseq \cfrac{v_0T_b}{2}\) です。これは速度 \(v_0\) と速度 \(0\) の平均速度 \(\cfrac{v_0+0}{2}=\cfrac{v_0}{2}\) で \(T_b\) 時間走行した結果，距離 \(D_b\) となったと解釈できます。

　例えば，上の棒グラフで時速100kmの場合，制動距離は84mでした。そこで，

\(v_0={\color{#ff0000}100} \cfrac{ \text{km}}{ \text{h}}={\color{#ff0000}100} \cfrac{1000 \text{m}}{3600 \text{s}} \)，\(D_b=84\)m

として，\(T_b \fallingdotseq\cfrac{2D_b}{v_0}\) から \(T_b\) を求めると，\(T_b\fallingdotseq 6\text{s}\) であったことがわかります。6秒は少し長いですが，車は急に止まれないことがよくわかります。

　ちょっと話が横にそれましたが，重要な話ですので，詳述しました。
　閑話休題。次回，運動方程式を使って海に投げ捨てられたはずの凶器が見つかった謎を解析します。

■ ダンロップの贈り物

　自動車や自転車には車輪が必須で，現在ではその車輪は空気入りのゴムチューブで囲まれている。その発想の原点はスコットランドの発明家，獣医師であったジョン・ボイド・ダンロップ（John Boyd Dunlop, 1840－1921）に遡る。タイヤのみならず，硬式テニスのボール「ダンロップフォート」，マッケンローが使用していたラケット「MAX200G」や最近はCXやSXシリーズ，あるいは，ゴルフなどでも有名なスポーツブランドでもある世界的企業DUNLOPの生みの親である。日本では出資率の関係で住友ゴム工業株式会社に社名が変更された。詳しくはダンロップのサイトを参照。

　Wikipediaによれば，ダンロップ氏は獣医師の発想で，病気の牛の腸が溜まったガスで膨らんでいたことを思い出し，ご子息の三輪車で空気入りのチューブ式タイヤの実験を行ったのが現在のゴムチューブタイヤの始まりとされる。木製の車輪の枠にゴムをつけただけの従来型のタイヤからの大幅な改良で，路面からの衝撃を和らげるものとして，車輪を使う乗り物のみならず，船舶の横にぶら下げたり，コースアウトした車のタイヤバリアなどにも使われている。4，50年くらい前には埋め込まれたタイヤを並べた遊具が学校の校庭や公園にあった。タイヤからタイヤへジャンプして遊んだり， 高鬼（たかおに。高い所にいれば鬼にタッチされても大丈夫という鬼ごっこの変種）に使ったりした。現在もあるのだろうか。

※「つい考えてしまう数学」の記事一覧はこちら