特集記事（高校）

　前回，ニュートンの冷却の法則をもとにして作った方程式（漸化式）を解いて，死亡時刻を推定しました。推理小説的には実は殺人事件だった，というのが定番ですので，今回もそれに則って話を進めましょう。

【証拠隠滅】

　犯人は殺人の証拠となる凶器を崖の上から海に投げ捨てました。下図のように崖の先端は崩落しそうだったので，少し手前の安全な場所から放り投げました。

　その後のストーリーは単純です。凶器は発見され，犯人は容疑者として目星をつけられ，刑事に尾行・追跡され，確保されました。
　このストーリーを，数学を用いて推論していきましょう。まずは準備の第一段階，速度と刑事の尾行について考えます。

【速度】

　\(x\) 軸上を動く点の位置を一定の時間間隔 \(τ \gt 0\) で記録します。\(n\) 番目に記録した時刻を \(t_n=nτ\) とし，そのときの点の位置を \(x_n\) としましょう。初期時刻は0で，初期位置は \(x_0\) です。以降，\(n=1,2,3\)  …と増えていきます。
　下図は，\(x\) 軸の正の方向に動いている車の先端の位置を時刻 \(t_n\) ごとに記録しているイメージ図です。

　時刻 \(t_n\) と動点の位置 \(x_n\) の組 \((t_n,x_n)\) を \(tx\) 座標平面上の点の座標としてプロットしていくと，下図のようになります。

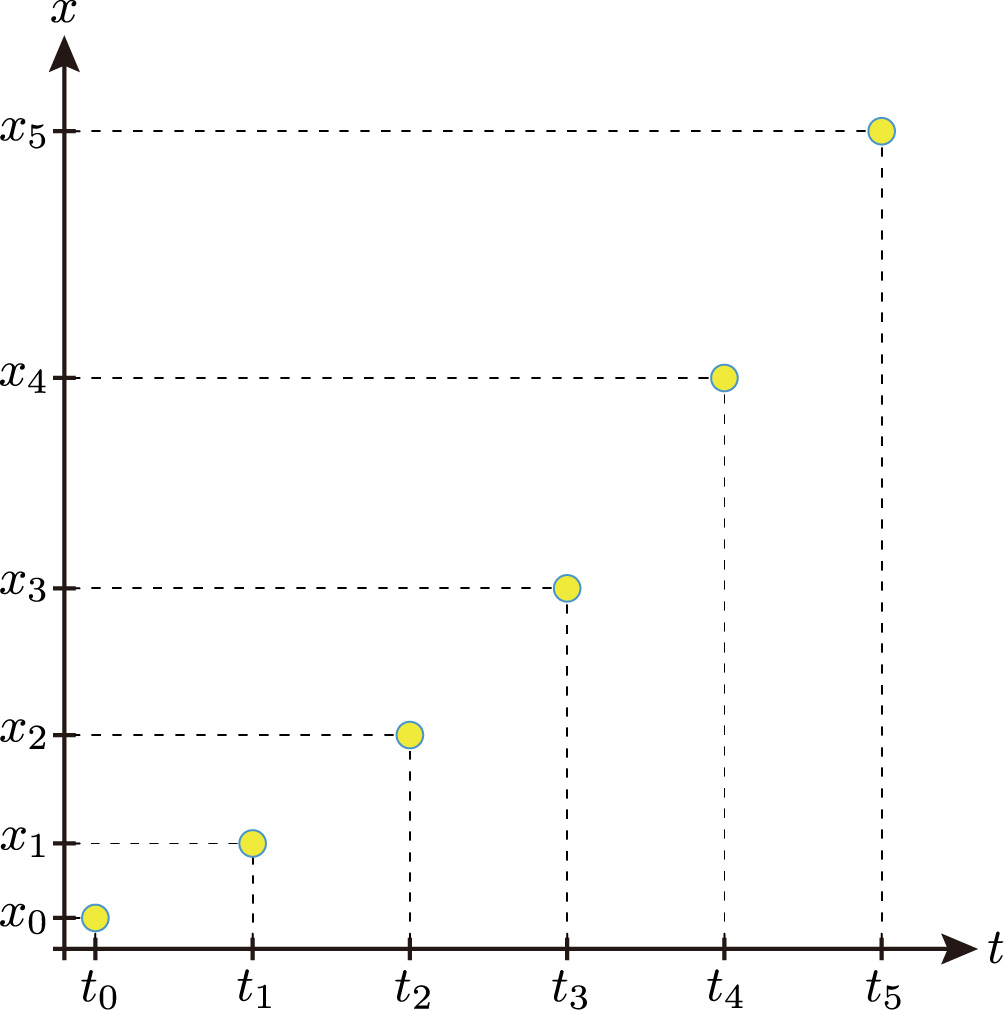
点 \((t_{n},x_n)\) 付近を拡大して，各点を線分で繋げると下図のようになります。

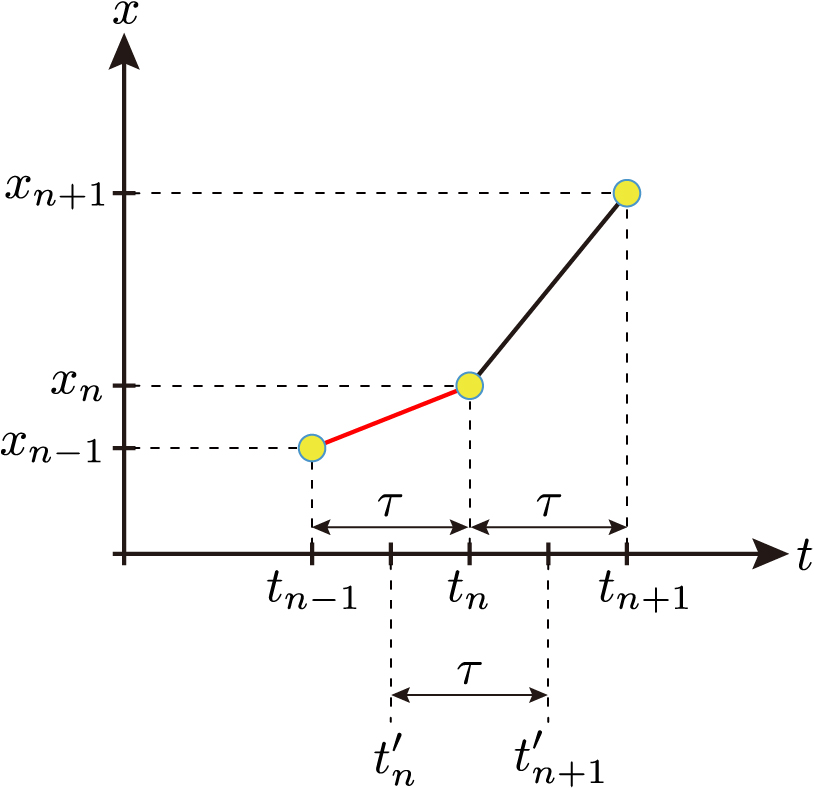
　位置の差 \(x_n-x_{n-1}\) は時刻 \(t_{n-1}\) から \(t_n\) の \(τ\) 時間に動いた距離です。これより，時間区間 \([t_{n-1},t_n]\) における位置の変化率を考えることができ，それを平均速度といって，

\(v_n=\cfrac{x_n-x_{n-1}}{τ} \ (n=1,2,3,\cdot \cdot \cdot)\)

と書きます。これは上の図における赤い線分の傾きに他なりません。\(v\) は速度（velocity）の頭文字です。

　時間区間 \([t_n,t_{n+1}]\) の中点を \(t’_n\) としましょう。上の図をみるとわかるように，時間区間 \([t_{n}^{\prime},t_{n+1}^{\prime}]\) の長さも \(\tau\) となります。時刻 \(t_{n}^{\prime}\) の瞬間の速度を計測することはできませんが，\(\tau\) が非常に小さければ，それはほとんど速度 \(v_n\) とみなせるでしょう。そこで，時刻 \(t_{n}^{\prime}\) の速度を \(v_{n}\) と定義します。

【例（等速直線運動）】

　\(x\) 軸上を等速度 \(c\) で動いている物体の速度は，

\(v_{n}=\cfrac{x_{n}-x_{n-1}}{\tau}=c \ (n=1,2,3,\cdots)\)

です。これより，

\(x_n=x_{n-1}+c\tau\)

\(x_{n-1}=x_{n-2}+c\tau\)

…

\(x_2=x_{1}+c\tau\)

\(x_1=x_{0}+c\tau\)

がわかります。よって，下の式を上の式に順次代入していくと，

\(x_{n}=x_{0}+nc\tau=x_{0}+ct_{n} \ (n=1,2,3,\cdots)\)

を得ます。よって，初期位置 \(x_0\) を決めれば時刻 \(t_n\) における位置 \(x_n\) がわかります。

【容疑者の尾行】

　容疑者は \(xy\) 座標平面上の \(x\) 軸上を正の方向に一定の速度 \(v_{s} \gt 0\) で移動しているとします。\(s\) は容疑者（suspect）の頭文字です。
　時刻 \(t_{n}\) における容疑者の位置を \(\text{Q}_{n}(q_{n},0)\) とすると，上の例での \(c=v_{s}\) の場合であるから，初期位置 \(q_{0}\) を決めれば，時刻 \(t_{n}\) における容疑者の位置 \(q_{n}\) が求まります。

\(q_{n}=q_{0}+v_{s}t_{n} \ (n=1,2,3,\cdots)\)

　一方，\(xy\) 座標平面上において，時刻 \(t_n\) の刑事の位置を \(\text{P}_n(x_n,y_n)\) とします。刑事は容疑者に気づかれないように，下図のように一定の間隔 \(d\) を保ちながら，容疑者を尾行しています。\(d\) は距離（distance）の頭文字です。

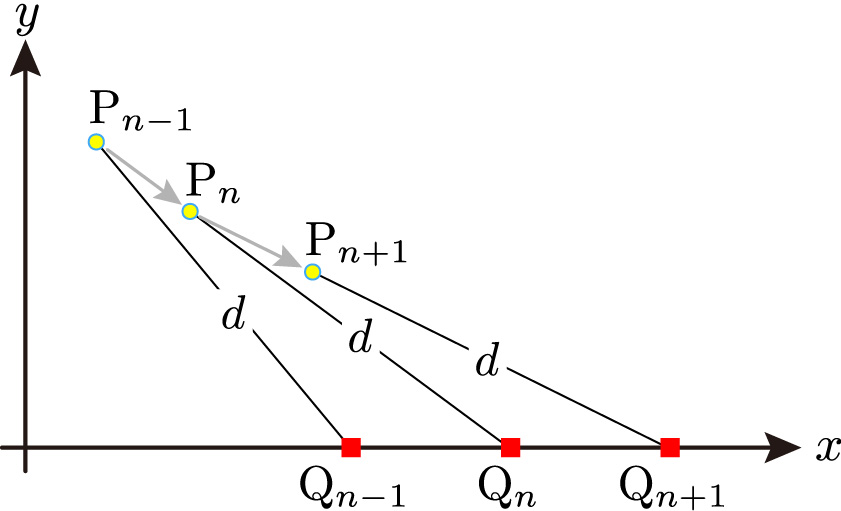
　刑事は容疑者が一定の速度で移動していることに気が付いているので，時刻 \(t_{n-1}\) で点 \(\text{P}_{n-1}\) にいた刑事は，次の時刻 \(t_{n}\) に容疑者が点 \(\text{Q}_{n}\) に移動することが予測できます。そこで刑事は，点 \(\text{P}_{n-1}\) から点 \(\text{Q}_{n}\) 方向に \(\tau\) 時間進んだ点 \(\text{P}_{n}\) に移動します。ただし，つねに \(\text{P}_{n}\text{Q}_{n}=d\) を満たすとします。\(\text{P}_{n}\text{Q}_{n}\) は点 \(\text{P}_{n}\) と点 \(\text{Q}_{n}\) の距離を意味します。これより，

\(\text{vec}(\text{P}_{n}\text{Q}_{n})=\lambda_{n}\text{vec}(\text{P}_{n-1}\text{Q}_{n}), \ \lambda_{n}=\cfrac{d}{\text{P}_{n-1}\text{Q}_{n}}\)

がわかります。ここで，\(\text{vec}(\text{P}_n\text{Q}_n)\) は点 \(\text{P}_n\) から点 \(\text{Q}_n\) へのベクトルを意味します。また，

\(\text{P}_{n-1}\text{Q}_{n}=\text{sqrt}((q_{n}-x_{n-1})^{2}+{y_{n-1}}^{2})\)

です。\(\text{sqrt}(x)\) は \(x\) の平方根（square root）です。

　これを成分表示すると，\(q_n=q_0+v_{s}t_n\) として，次のようになります。

\(q_n-x_n=\lambda_n(q_n-x_{n-1})\)

\(-y_n=\lambda_n(-y_{n-1})\)

　これが解くべき漸化式です。少々複雑なので，簡単に解 \((x_n,y_n)\) を表示することはできないでしょう

　そこで，具体的な値をいれてシミュレーションしてみました。
　下図は，容疑者と刑事の間隔を \(d=10\)，刑事の初期位置 \(\text{P}_0\) を \(y\) 軸上で \(y_0=d( \ x_0=0 \ )\)，容疑者の初期位置 \(\text{Q}_{0}\) を原点( \(q_{0}=0\) )，容疑者は歩行速度 \(v_{s}=1\) で動き，時間間隔を \(\tau=1\) とし，漸化式

\(q_n=v_st_n\)

\(\lambda_n=\cfrac{d}{\text{sqrt((}q_n-x_{n-1})^2+{y_{n-1}}^2)}\)

\(x_n=q_n-\lambda_n(q_n-x_{n-1})\)

\(y_n=\lambda_ny_{n-1}\)

を \(n=1,2,3,\cdots,30\) まで順次計算してプロットした図です。

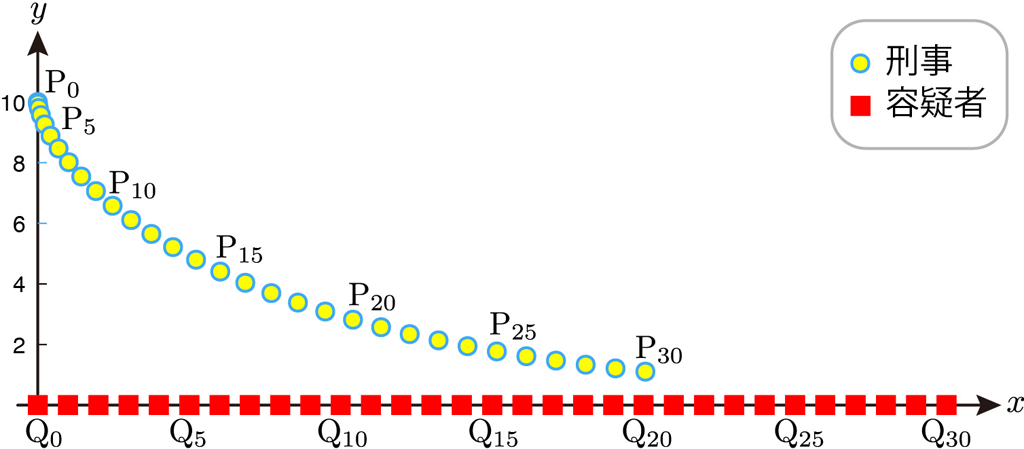
　\(t_n=30\) あたりから，ほぼ容疑者の真後ろに10だけ離れて尾行していることになります。
　ところで警察はどのように容疑者にたどり着いたのでしょうか。それは凶器の証拠物を発見したからです。では海に投げ捨て沈んだと思われたはずの凶器はどうして発見されたのでしょうか。続きは次回。

■ ヨハン・ベルヌーイの贈り物

　等速直線運動は永遠に一直線ならば上述したように式で書けるので，到達時刻も正確に求めることができる。しかし，途中で曲がるようなことがあると，途端に難しくなる。例えば，砂浜にいるライフセーバーが海に溺れている人を助けることを考えよう。

　下図のようにライフセーバーは砂浜を走り，海を泳いで救助に向かうとき，ルートが3パターンあるとする。最短時間を目指して到達するにはどのルートで救出に向かうべきだろう。

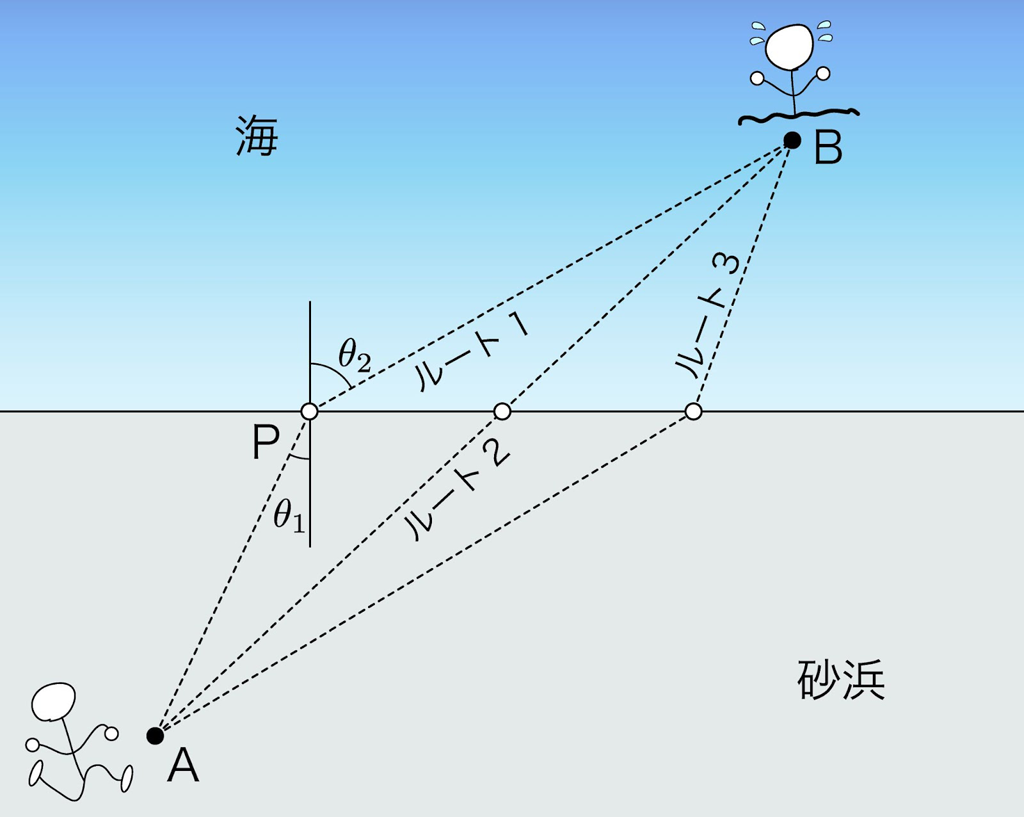
　砂浜を走るほうが海を泳ぐより速かったら，海で泳ぐ時間を減らすようにルート3を選べば良いし，逆だったらルート1。同じ速さだったら直線でいけばよいからルート2。

　これはいわゆるフェルマーの原理の問題である（Pierre de Fermat，1607－1665［仏］）。正確な場所は，砂浜の移動速度を \(v_1\) とし，海で泳ぐ速度を \(v_2\) としたとき，図の角度をつかって，

\(\cfrac{\sin \theta_1}{\sin \theta_2}=\cfrac{v_1}{v_2}\)

を満たす地点である。この式はスネルの法則と呼ばれる（Willebrord Snell，1580－1626［オランダ］）。

　ヨハン・ベルヌーイ（Johann Bernoulli，1667－1748［スイス］）は旅人が歩きやすい土地から荒れて歩きにくい土地を歩く問題として，1691年の彼の微分学の教科書に出題している（下図：左下から右上に歩く）。

※「つい考えてしまう数学」の記事一覧はこちら