特集記事（高校）

全体の傾向

　2025年の大学入試における「統計的な推測」の出題は，旧課程の浪人生への対応もあってか，限定的なものになりました。主な出題をまとめたのが次の表です。

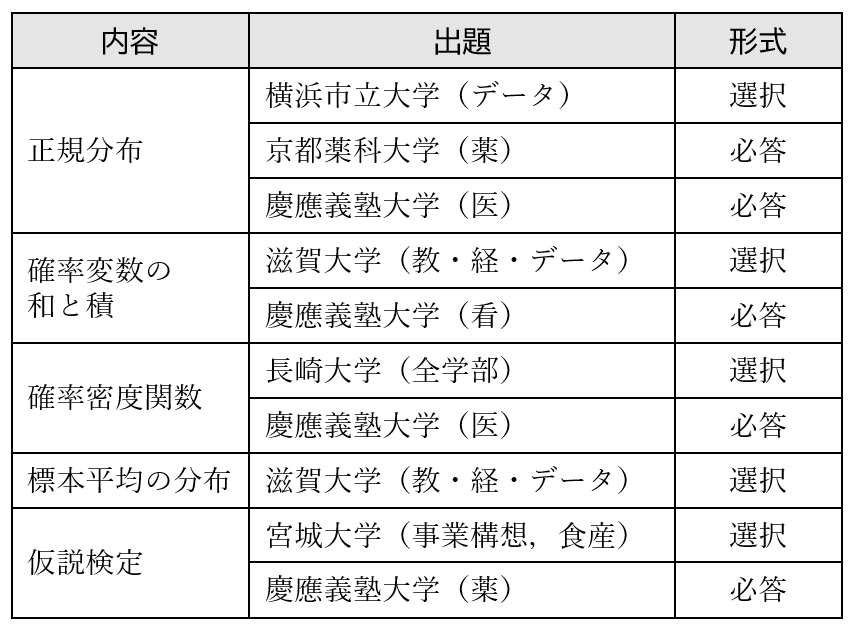
　特に力が入っていたのは慶應義塾大学で，学部ごとに問う内容を変えたうえで必答問題として出題しています。
　以下，対策が必要と感じられたいくつかの問題を取り上げました。

確率密度関数

　両問とも，“確率密度関数のグラフと\(x\) 軸の間の面積が1”であることは前提の知識として扱われています。「統計的な推測」の学習時に数学Ⅱの積分を学んでいない場合，確率密度関数の扱いはどうしても軽くなるので，入試対策で改めて押さえたいところです。
　長崎大学の問題の後半は，積分で見られる“面積比からの積分区間の決定”問題に似たつくりになっていて融合的です。

確率変数の和と積

　教科書における“確率変数の和と積”の性質は，二項分布や標本平均分布の平均・分散の導出に用いられるほかは，例や例題で具体的な数値で計算するものが主です。
　この慶應義塾大学の問題のように文字のみで性質を利用する問題は，初見だと戸惑う可能性があるでしょう。

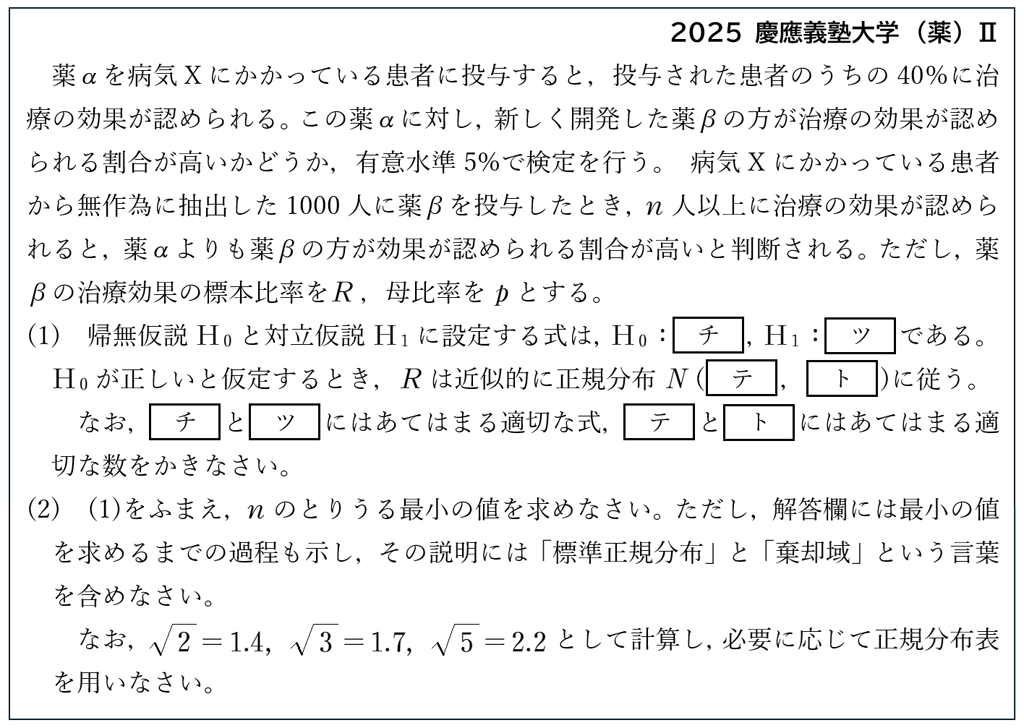
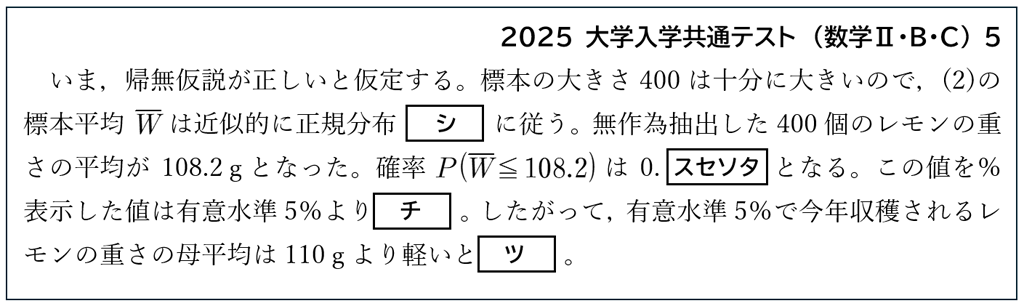
仮説検定

　仮説検定は手順が決まっているため，教科書の例題・節末問題と同じような内容にとどまっています。しかし，上の問題では，どちらも棄却域を利用して考えている点に注意が必要です。
　2025年の共通テストの仮説検定では，”\(p\) 値と有意水準の比較”によって棄却を判断していました。入試対策としては，どちらの方法でも判断出来るようにしておくのが望ましいようです。