特集記事（高校）

　みなさん，こんにちは。暑くなってきましたが，いかがお過ごしでしょうか。自分が受験生のころとは気候がまったく違い，今の受験生たちにはエアコンが必須ですね。
　さて今回は，前回の『場合の数の基本』に続きまして，『確率の基本』です。よろしくお願いします。

確率の原則

　この分野の指導において，まず重要なのが『場合の数』と『確率』の考え方の違いです。基準の違いと言ってもイイでしょう。

　例えば，袋の中に赤玉1個と白玉99個が入っていて，この中から1個の玉を取り出すとき玉の取り出し方の総数は「赤玉か白玉」の2通りです。だからと言って，赤玉を取り出す確率が \(\frac{1}{2}\) というわけではありません。

　つまり，「場合の数」では各事象が等確率で起こるかどうかはまったく気にしていないわけですが，「確率」では等確率で起こる事象を設定することが（学習初期段階では）重要になるということです。

　このことに注意するために，確率の問題を解くときにはすべてのものを区別して考えることが原則です。上記の例であれば，玉をすべて区別して，赤玉，白玉1番，白玉2番，…，白玉99番の100個と考えて，取り出し方の総数を100通りとすればよいわけです。

　よく次のような解答・解説を見かけます。

　間違っているわけではありませんよ。でも，大山はモヤモヤします。

　生徒が書くのはともかく，指導者がこの解答を書いていたら，生徒は混乱すると思います。なぜなら，\({}_n \mathrm{ C }_k\) は「異なる \(n\) 個のものから異なる \(k\) 個のものを選ぶ組合せの総数」を表しているのですから。

　つまり，この解答は上記の原則を暗黙の了解としてしまっているのです。学習が進んで生徒たちが十分に慣れたら，このような解答でも構わないかもしれませんが（それでも大山は書きません），少なくとも初期段階ではすべてのものを区別することを強調しておくべきです。

　したがって，大山は解答の最初に「すべての玉を区別して考える。」という一文を入れ

などと板書します。

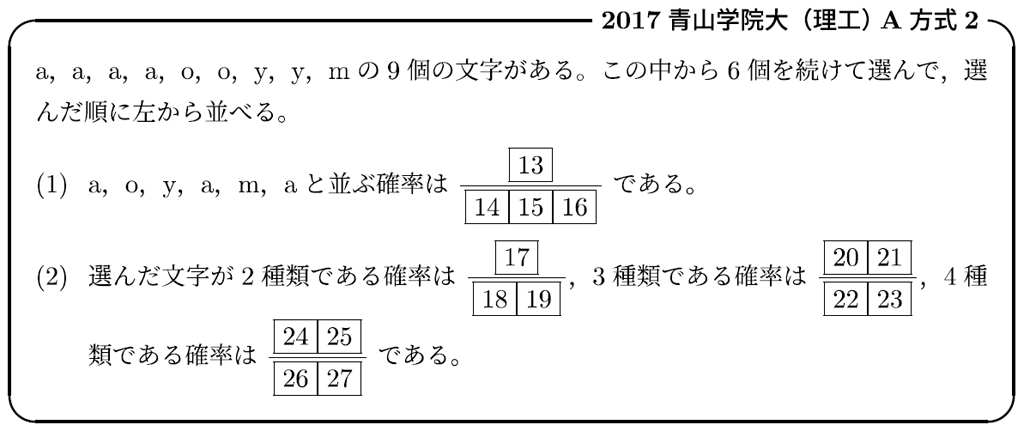
　このような原則の理解（と，前回お話しした「選ぶ」と「並べる」）を試すことができる問題として，大山がよく使っているのが（少し古くなってきてしまいましたが）次の一題です。

　また，この問題では「安易に余事象を利用するな！」という話もします。（解答例はこちら）

反復試行の確率

　意味も分からずに丸暗記している生徒を毎年観測します。この公式は，事象が「\(A\) とその他 \(\overline{A}\) 」という2つの場合のシンプルな問題にだけ適用できる公式であって，決して万能ではありません。したがって，丸暗記状態ではまったく応用できません。

　やはり，しっかりとこの公式の意味を教えておきたいし，3つ以上の事象を考える複雑な問題になっても対応できるように指導しておきたいところです。

　例えば，次のような問題を考えてみましょう。

　大山は次のように解説しています。
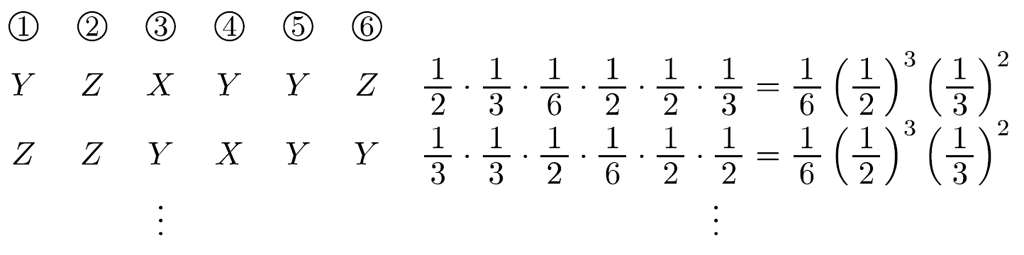
　まず，1回の試行における事象（とその名前）を設定し，各事象の起こる確率を求めておきます。例えば　

としておきます。
　そして，順番を指定した場合の確率をいくつか確認します。例えば

という感じで。これで生徒たちに順番が変わっても確率は変わらないと気づいてもらえればОＫです。

　あとは，この「場合分け」が全部で何通りあるか分かれば全部の確率を足すだけです。

　\(X，Y，Y，Y，Z，Z\)の順列は，「同じものを含む順列」の考え方で

\(\cfrac{6!}{3!\cdot 2!}\)（通り）

あるいは，前回紹介した「席選び」で

\(6\cdot {}_5 \mathrm{ C }_3=60\)（通り）

なので，求める確率は

となります。

　したがって，大山は「反復試行の確率」を

（順列の総数）×（1順列の確率）

と説明しています。
　難関大を目指す生徒に考えさせたい問題がこれです。

　公式の丸暗記では対処できませんし，事象の設定に工夫が必要です。（解答例はこちら）

条件付き確率

　一般に，事象 \(A\) が起こったときの事象 \(B\) が起こる確率（条件付き確率）  は\(P_{A}(B)\) は

\(P_A(B)=\cfrac{n(A \cap B)}{n(A)}=\cfrac{P(A \cap B)}{P(A)}\)

で得られます。したがって，「\(n\) 分の \(n\)」と「\(P\) 分の \(P\)」のどちらでもイイので，ウマく使い分けられると効率的です。
　 例えば次の問題では，大山は「\(n\) 分の \(n\)」で考えるのが好きです。

　隣り合わないものは後からスキマに入れるというのも知っておくべき手法ですね。（解答例はこちら）

　また， \(P_{A}(B)=\frac{P(A \cap B)}{P(A)}\) の分母を払って

\(P(A) \cdot P_{A}(B)=P(A \cap B)\)

の形にできます。

　これは，「状況 \(A\) になる確率」と「状況 \(A\) のとき状況 \(B\) になる条件付き確率」の積が「状況 \(A\) を通って状況 \(B\) に至る確率」に等しいと解釈できます。したがって，  は「状況 \(A\) から状況 \(B\) への推移確率」を表していると考えられます。

　確率漸化式の授業をする前に一度このことを確認しておくと，推移図などの概念が伝わりやすいでしょう。

---

　第9回は以上になります。『場合の数』も『確率』も，覚えるべき基本事項は少ないけど，ちょっと設定が変更されただけで解き方が全然変わってしまう分野です。その為，「正確に題意を把握する力」と「実験などによる計算方法の発見」が要求されます。しっかりと演習量を確保させたい分野ですね。

　次回は，「不等式の意味」について書きたいと思います。暑い日が続きますが，体調に気を付けて頑張りましょう!