
(前編はこちら)
【最初の疑問の回答】棒を壁に沿ってすべらせたときと同じように考えます。縦の長1,横の長さ \(a (0\lt a \lt 1)\) の長方形を移動させます。左側の縦の辺を青色,右側の縦の辺を緑色とし,長さ1の青辺と \(x\) 軸のなす角度を \(t\) とします。このとき,青辺の \(y\) 軸上の端(白丸)の \(y\) 座標は \( \sin t\) となり,\(x\) 軸上の端(黄丸)の \(x\) 座標は \( \cos t\) となります。\(t\) は \(\frac{\pi}{2}(90^\circ )\) から \(0(0^\circ)\) まで動きます。
青辺が動くと,それと同時に緑辺も動きます。緑辺が点 \(\text{A}\) にぶつかったらアウトです。
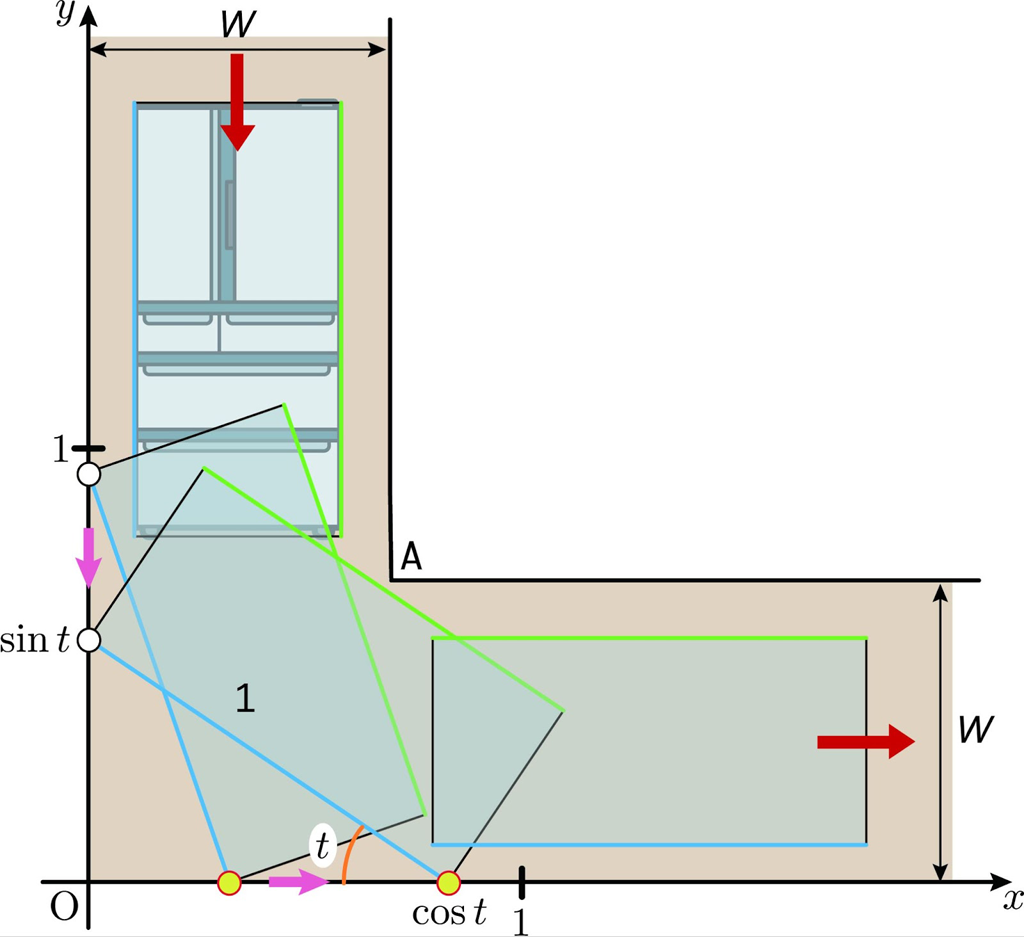
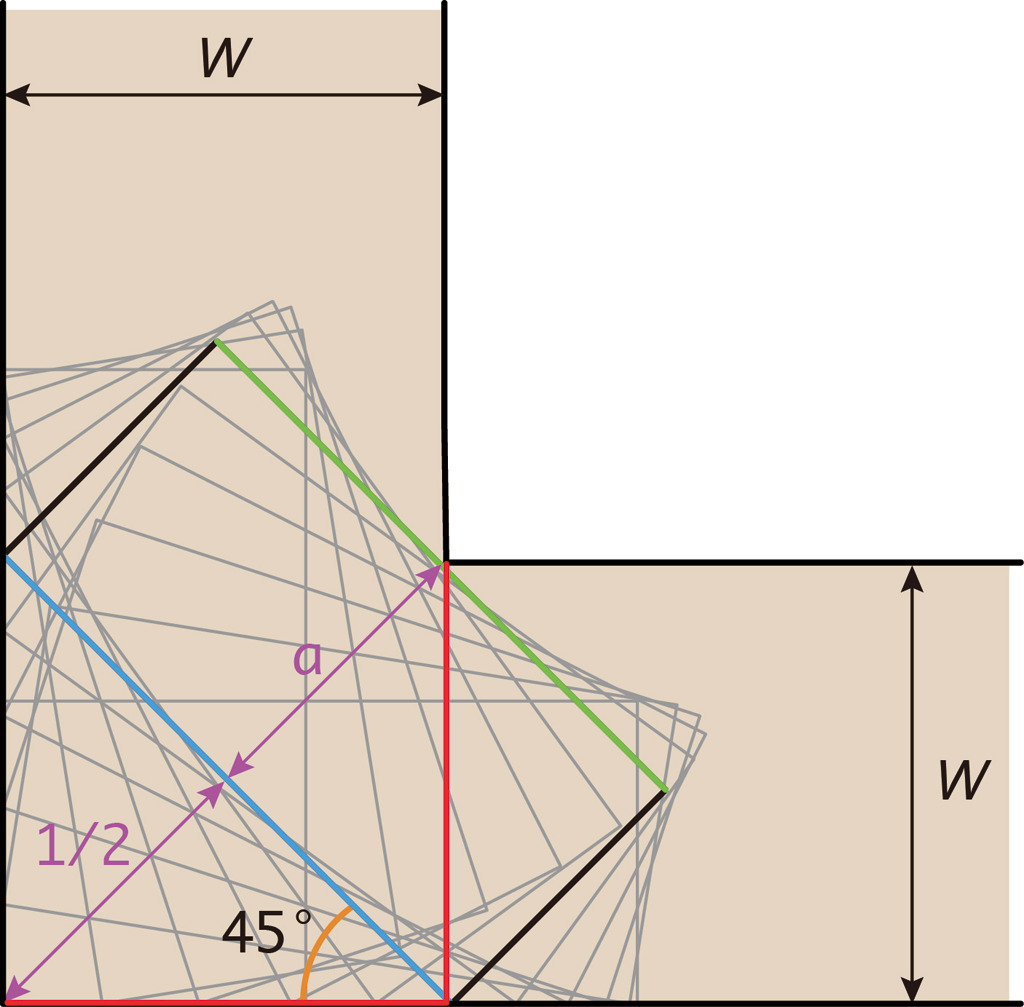
点 \(\text{A}\) の方向 \((1, 1)\) にもっとも長方形が突き出るのは,\(45^\circ(t=\frac{\pi}{4})\) のときです。このとき,緑辺が点 \(\text{A}\) に接するとします。下図の青辺の長さは1なので,赤い直角が作る直角二等辺三角形の斜辺の長さは \(a+\frac{1}{2}\) です。だから,\(W\) の大きさは,\(W=\frac{a+\frac{1}{2}}{\sqrt{2}}\) になることがわかります。これが求める下限です。\(a\rightarrow 0\) の極限で\(W\rightarrow\frac{\sqrt{2}}{4}\) となり,棒のときの結果に一致します。
上でみたように,長方形の青辺の集まりから浮き彫りになる,下図の赤色の包絡線はアステロイドです。緑辺の集まりから浮き彫りになる青色の包絡線はどんな曲線でしょうか。
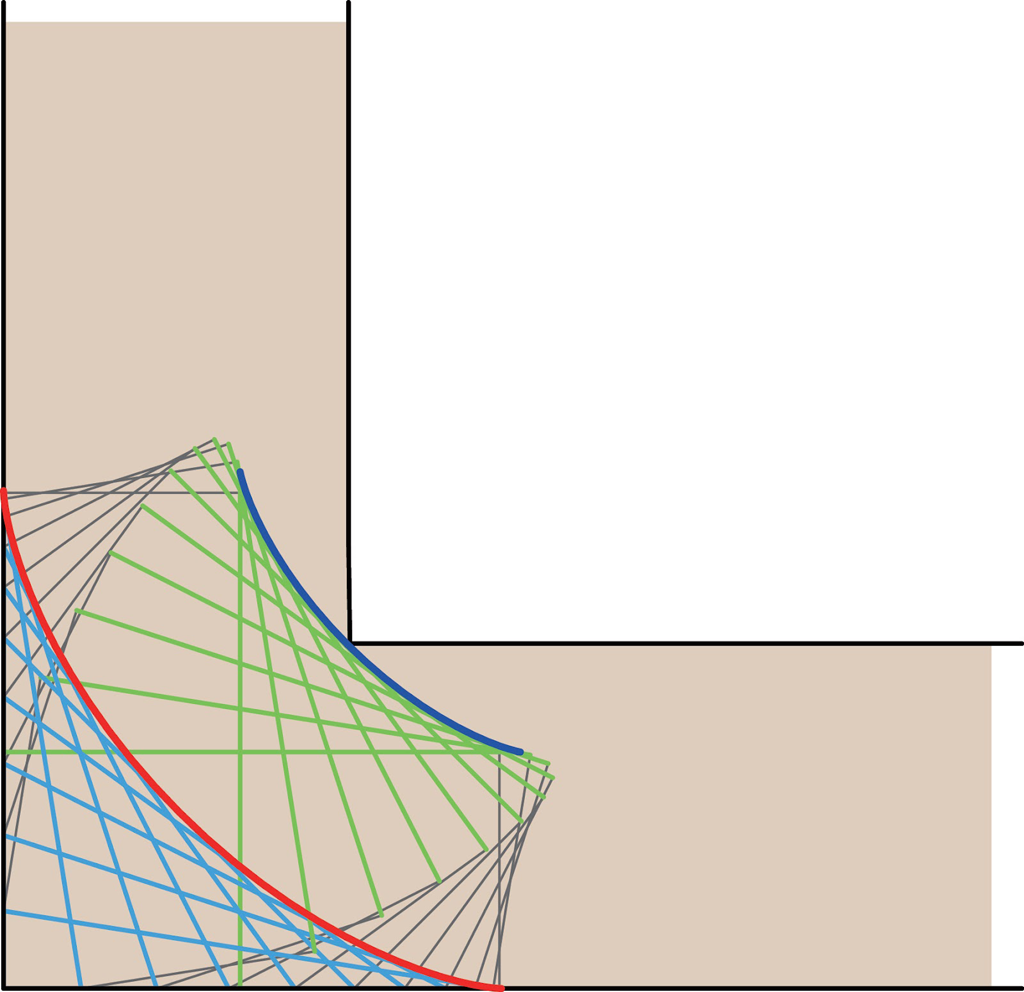
長方形の右側の緑辺は,左側の青辺を,下図の黒矢印の方向に平行移動したものです。左側の青辺は \(x\) 軸となす角度が \(t\) ですので,黒矢印ベクトルは,大きさが \(a\) で,方向は \((\sin t, \cos t)\) です。\(a\) の値は,冷蔵庫のイラストの大きさに合わせて,\(a=0.477\) にしました。
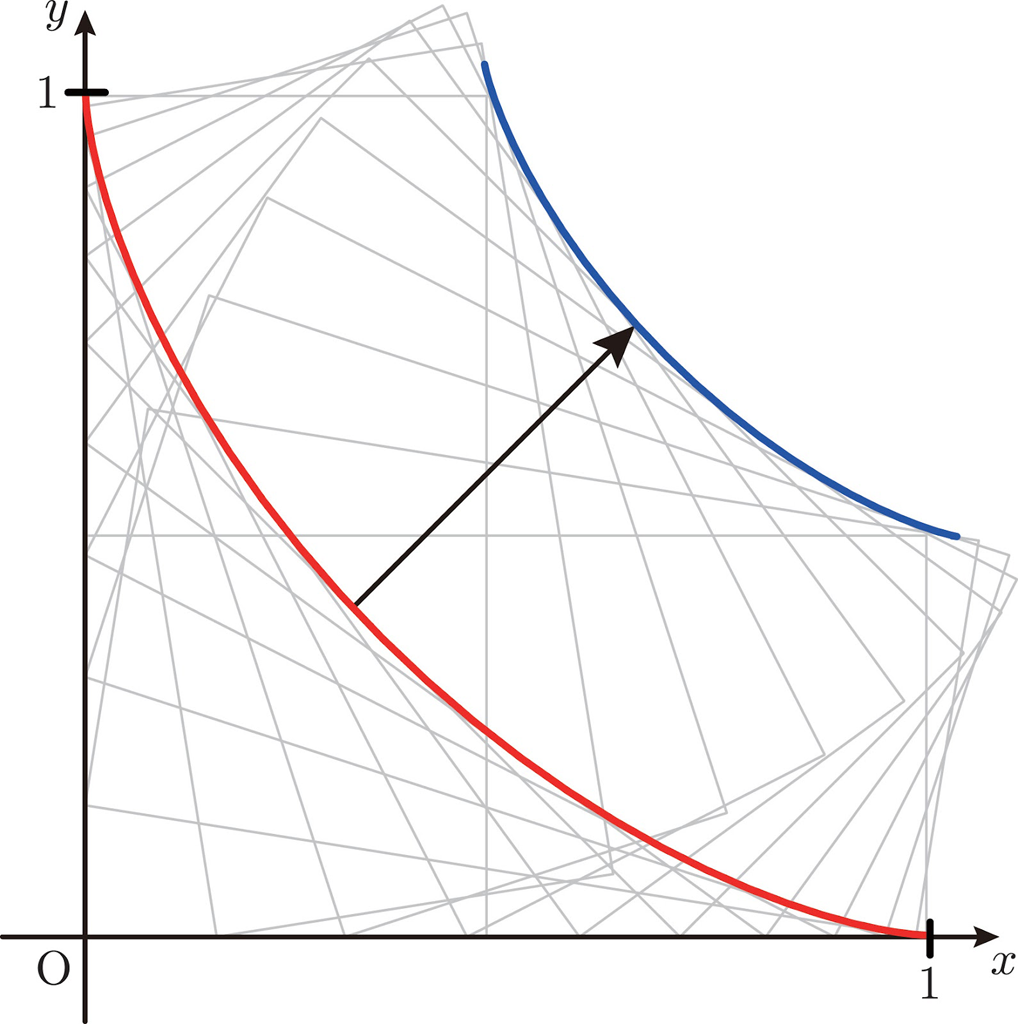
青色の包絡線は,赤色の包絡線(アステロイドの一部)に \(a(\sin t, \cos t)\) を加えたパラメータ表示になります。
よって,青色の曲線は \((\cos^3 t,\sin^3 t)+a(\sin t, \cos t)\) とパラメータ表示されます。\(t\) を \(0(0^\circ)\) から \(2{\pi}(360^\circ)\) まで動かすと下図のようになります。アステロイドとは異なります。また,青色の曲線の第1象限と第3象限の部分は赤色のアステロイドをずらしただけのようにみえますが,曲がり具合が異なります。
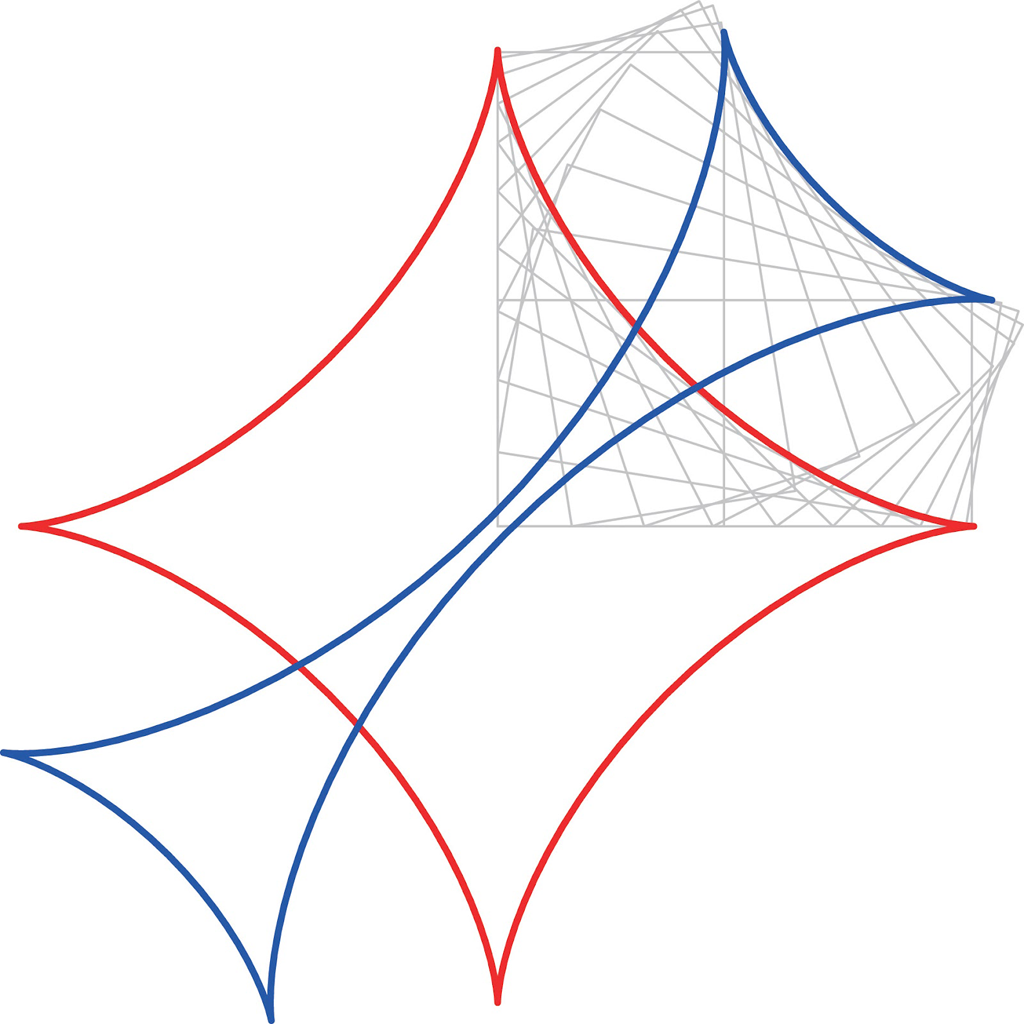
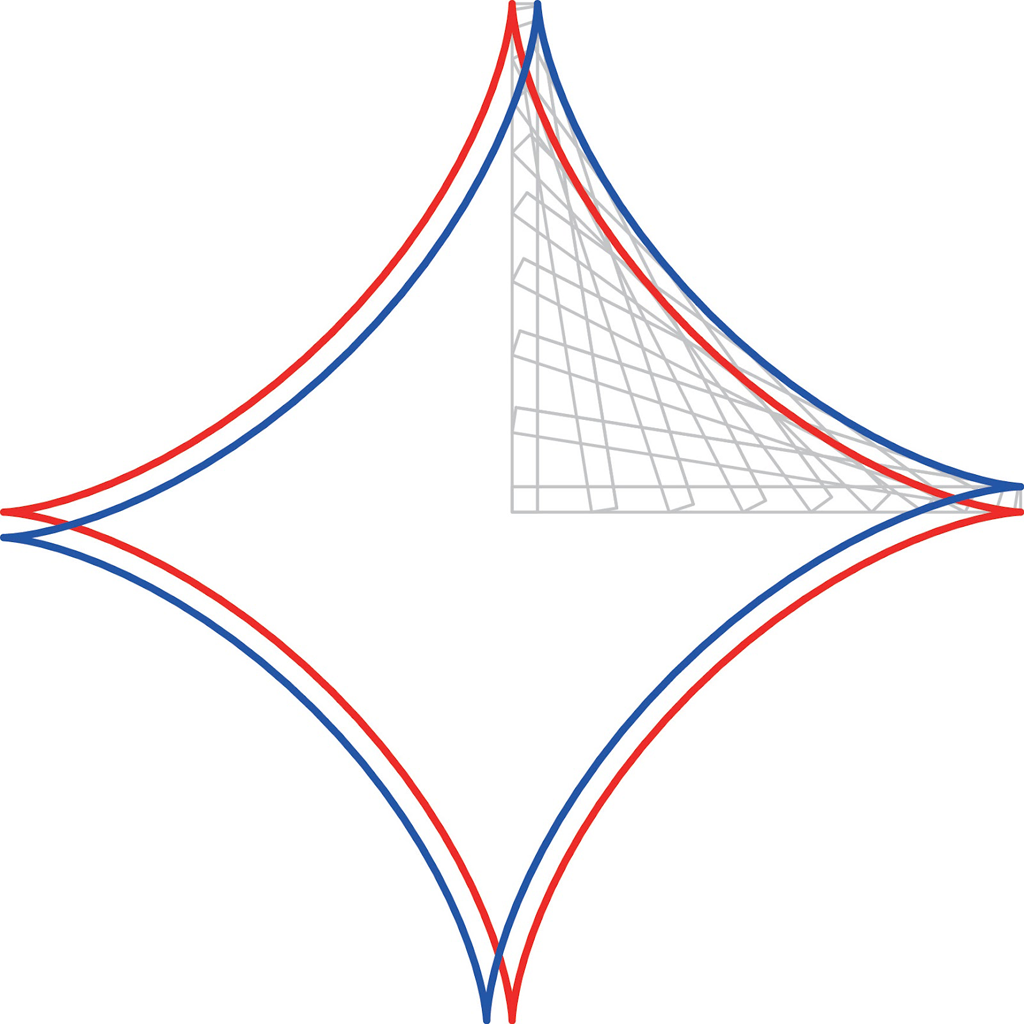
もっと \(a\) を小さくしてみましょう。\(a=0.05\) くらいにすると,黒板や大きな絵画など,上からみたらほぼ棒を動かすのと同じようになります。実際,下図のように青色曲線は,ほぼ赤色のアステロイドと同じ形状にみえます。
最大限 \(a\) を大きくしてみましょう。\(a=1\) の場合は,正方形を動かすことになります。このとき,青色曲線は下図のようになります。
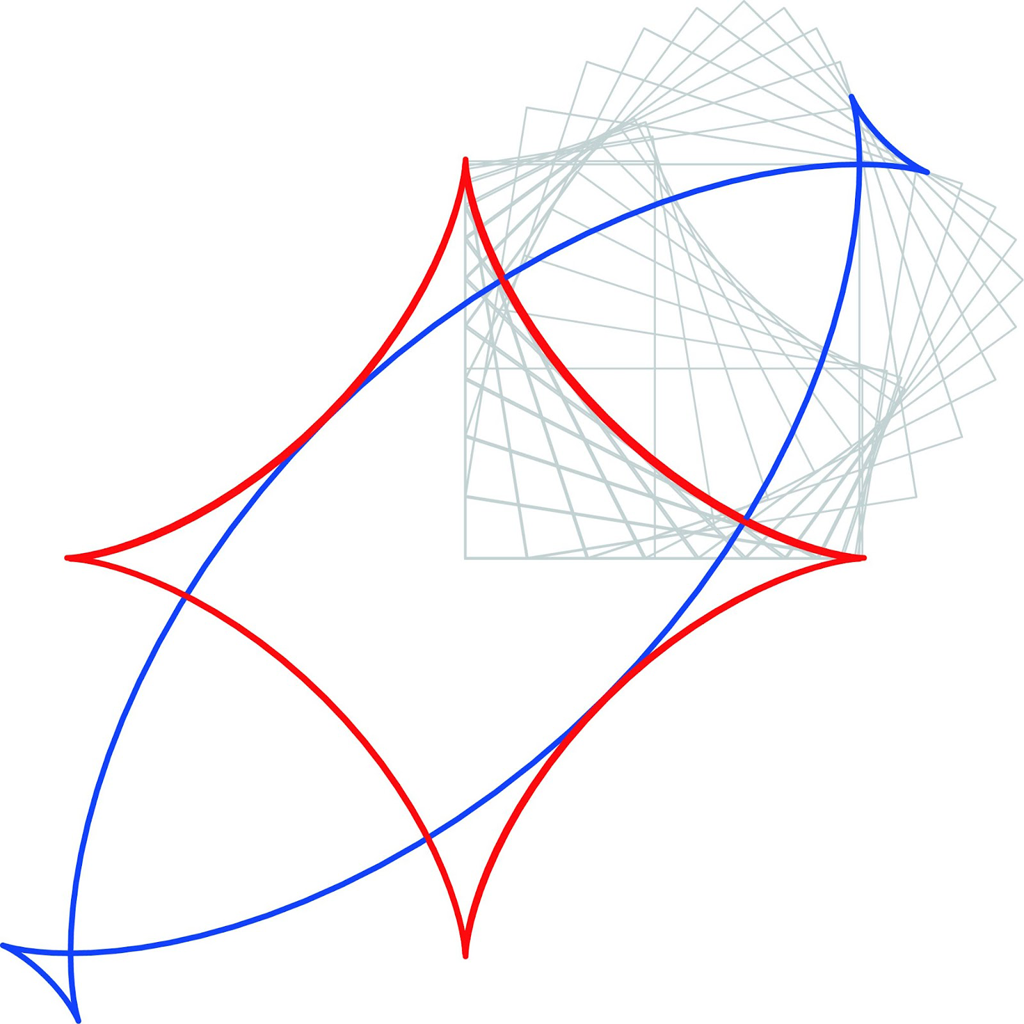
\(a=1\) の正方形の場合,\(W=\frac{1+\frac{1}{2}}{\sqrt{2}}=\frac{1.5}{\sqrt{2}}\gt 1\) なので,幅が \(a=1\) よりも大きい通路が必要です。この場合は,下図のように正方形を回転させなければ,少しだけ狭い幅が \(W=1\) の通路で十分なことがわかります。
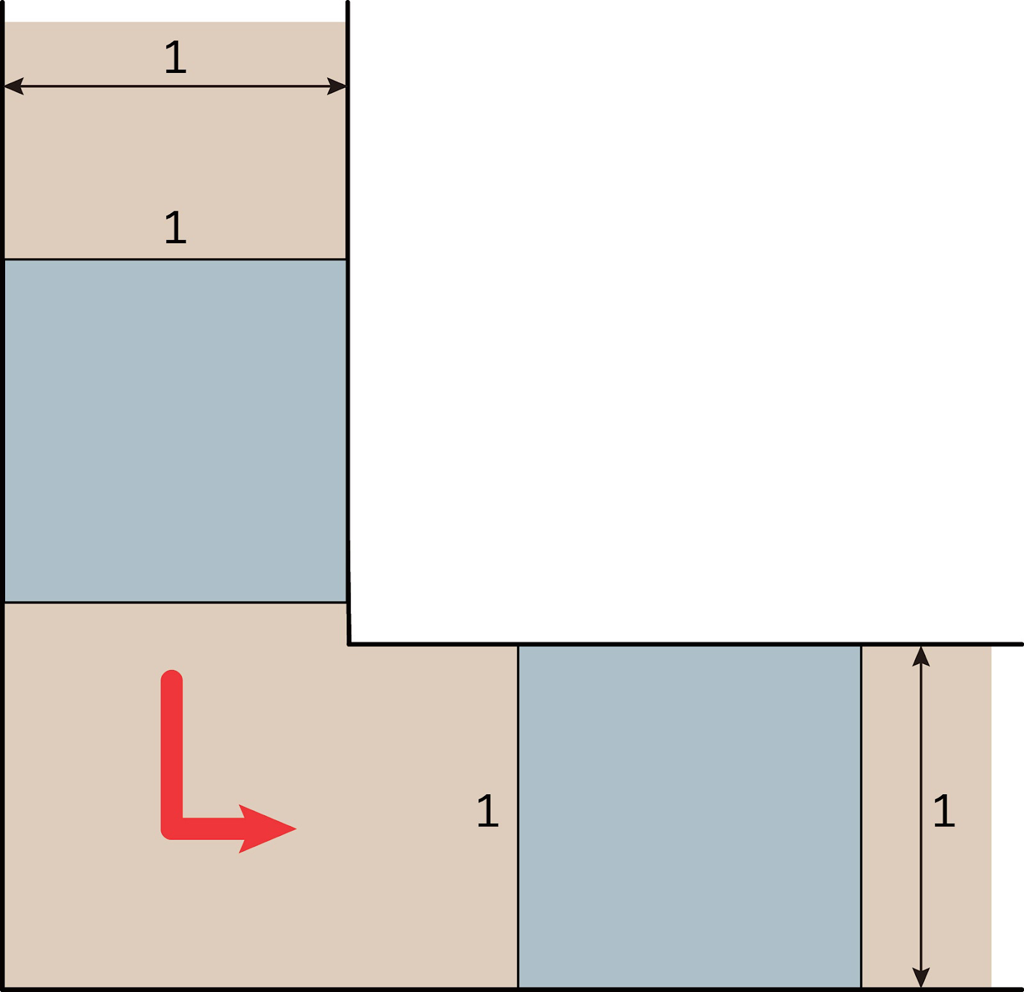
つまり,最初の【疑問】に \(W=\frac{a+\frac{1}{2}}{\sqrt{2}}\) が下限であると回答しましたが,これは長方形の動きを制限した場合の答えであることがわかりました。\(W=\frac{a+\frac{1}{2}}{\sqrt{2}}\)が最小値となるように【疑問】を修正しておきましょう。
【修正した疑問】\(1\text{:}a\) の長方形の左側の2頂点を壁に接したまま回転させた場合の \(W\) の最小値は何か。
\(W=1\) とします。このとき, \(1=\frac{a+\frac{1}{2}}{\sqrt{2}}\) を \(a\) について解くと,\(a=\sqrt{2}-\frac{1}{2}=0.9142⋯\lt 1\) です。だから,【修正した疑問】のように動きを制限した場合,\(a=1\) の単位正方形よりも面積が小さい長方形が答えになります。しかし,上図のようにスライドさせた動きをすれば,単位正方形が答えになりました。
単位正方形の面積は1です。これよりも,大きな図形は考えられるのでしょうか。
【疑問の深掘り】動き方を制限せず,形状も制限しない場合,幅1のL字通路を運搬できる面積が最大の図形は何か。
ハマーズリーの贈り物
【疑問の深掘り】はしばしば『ソファー問題』と呼ばれます。1966年にモーザーにより提出されましたが,それ以前にも類似の問題は投げかけられていたようです。
ソファー問題の解決第一歩として,単位正方形よりも面積が大きい図形は半径1の半円であることがわかります。
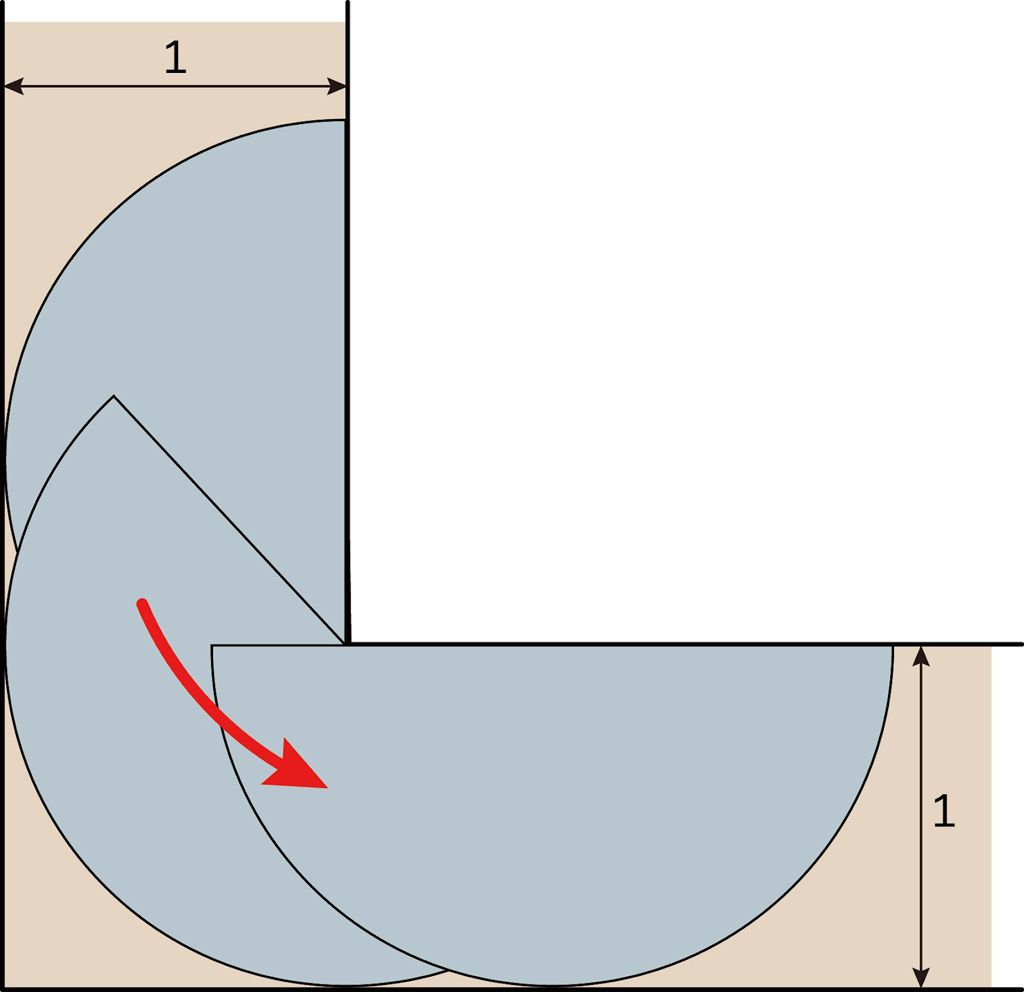
面積は\(\frac{\pi}{2}=1.57⋯ \gt1 \) ですから,半円は確かに単位正方形よりも面積が大きいです。
イギリスの数学者ハマーズリー(John Michael Hammersley(1920-2004)。超一様分布列(Low-discrepancy sequence)におけるハマーズリー集合などに名を残している)は,さらに面積が大きい図形を考案しました。
直径 \(\frac{4}{\pi}\) の半円をくりぬいた \(\frac{4}{\pi}:1\) の長方形の両脇に半径1の四分円を2つくっつけた受話器のような形の図形を考え出しました。面積は \(\frac{\pi}{2}+\frac{2}{\pi}=2.207⋯\) です。かなり大きくなりましたね。
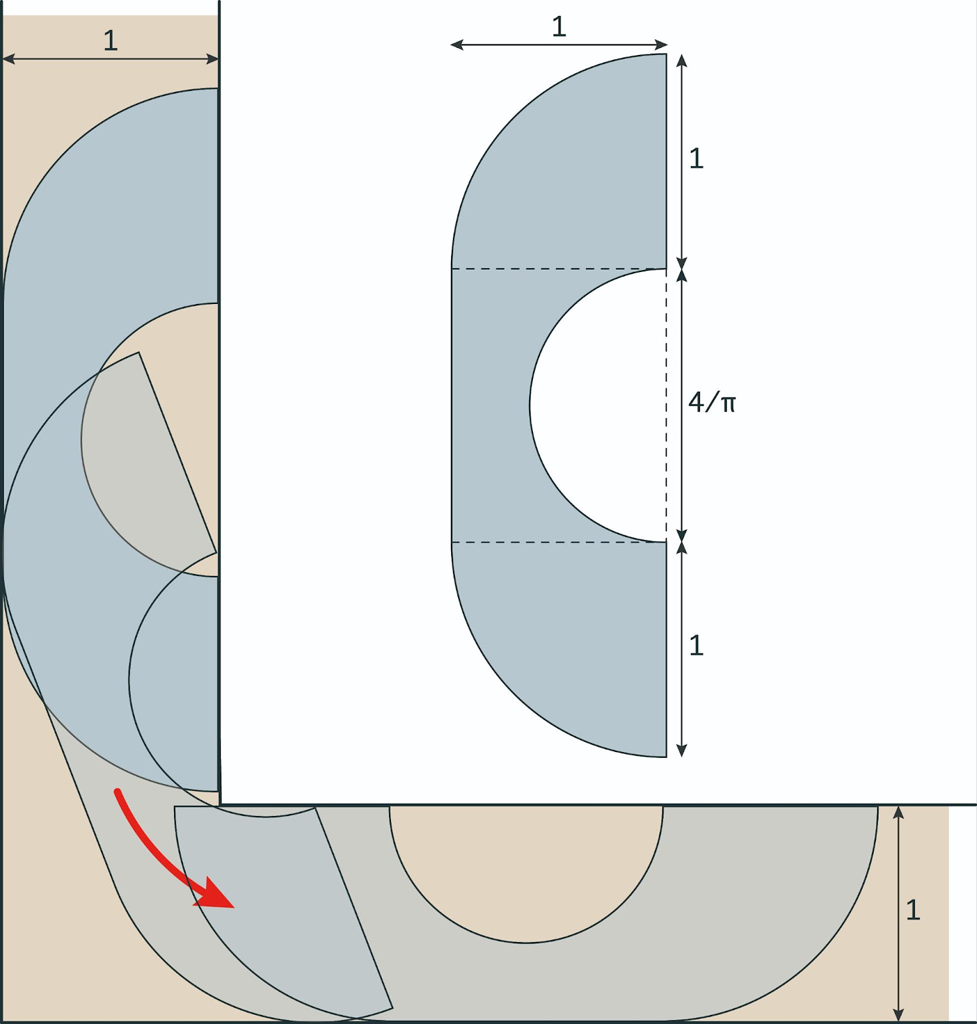
ハマーズリーの受話器型ソファーは画期的でした。長らくこの形を超える形は出てきませんでしたが,1992年にガーバーが受話器型の角を取って,さらに洗練させた面積 \(2.21953166887・・・\) の形状を提案しました。現在,ガーバーのソファーがソファー問題の答であるという証明がプレプリントサーバーarXivに提出されています。詳細はウィキペディア『ソファ問題』を参照するとよいでしょう。
ハマーズリーの受話器型ソファーはベストではなかったけれども,ほとんどベストに近いものでした。
数学の証明もそうですが,最初にブレークスルーとなる革新的なアイディアを考え出すことは,たとえ完全でなくても,それ自体とても重要で,敬意を表すべきことです。ニュートンだって,オイラーだって,フーリエだって,彼らの数学には現代からみたら些細なミスや不完全さもありましたが,そんなことより時代を変える新たな数学をつくったのですから。
※「つい考えてしまう数学」の記事一覧はこちら
1970年東京生まれ。早稲田大学理工学部数学科卒業。東京大学大学院数理科学研究科数理科学専攻博士課程修了。現在,明治大学理工学部数学科専任教授。博士(数理科学)。専門は応用数理,特に界面現象の数理解析。実験を採り入れた数学の講義で定評がある。
| 著書: | 『実験数学読本』①・②・③ (日本評論社),『次元解析入門』,『界面現象と曲線の微積分』,『動く曲線の数値計算』(以上共立出版),『大学数学の教則』(ちくま学芸文庫),『公式は覚えないといけないの?』(ちくまプリマー新書),他。 |
その他のコンテンツ
