
冷蔵庫やソファーなどの大きなものの搬入,搬出,あるいは移動といった,建物内の荷物の運搬は,引っ越しのシーズンに限らず,日常的にどこかで行われています。
建物によってはL字の通路を運ばなくてはならないこともあるでしょう。

横に寝かせた冷蔵庫やソファーなどは,真上から見ると長方形の物体とみなせます。長方形を壁にあたらないようにL字通路を通過させることを考えましょう。
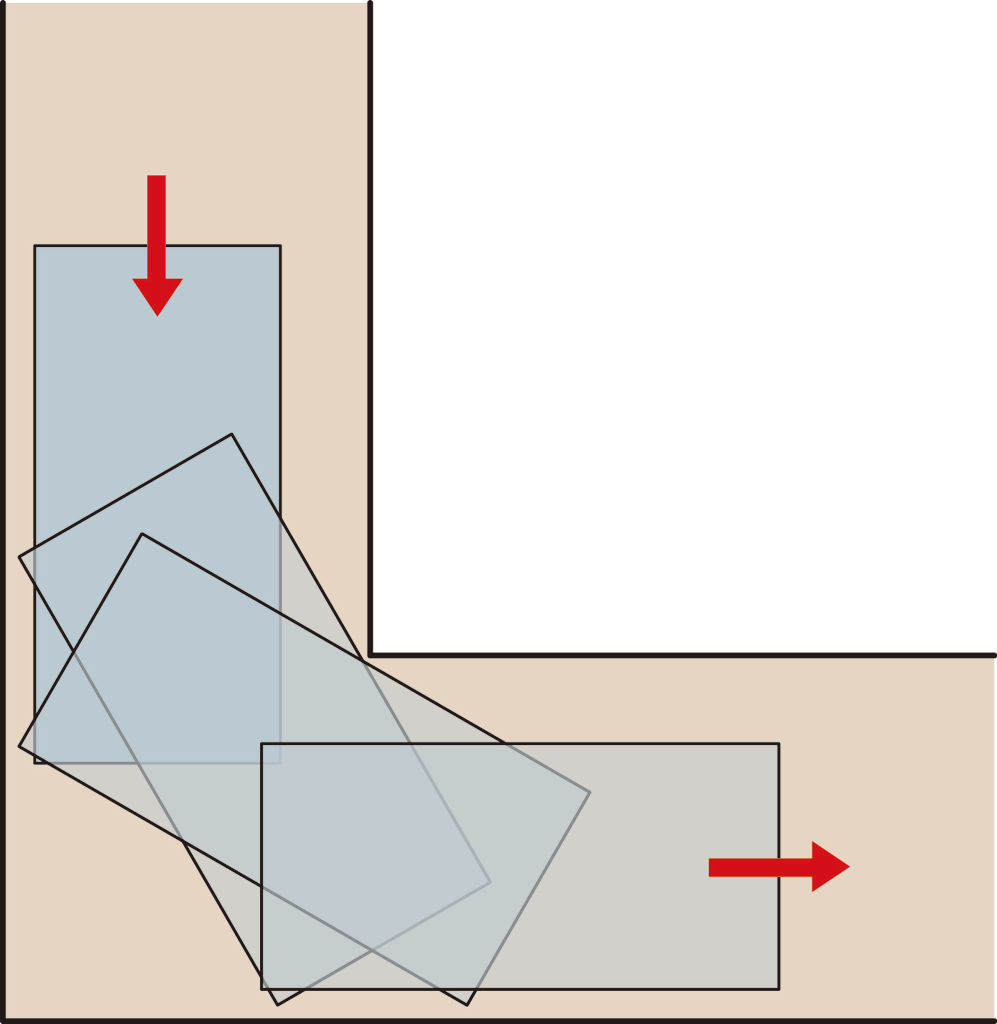
【注意】実際は,鉛直方向の空間を使って物体を斜めに傾けて運搬することも多いですが,問題がややこしくなるので,いまは平面上の問題に特化した設定にします。
長方形物体の長辺の長さを1とし,短辺の長さを \(a\) とします。また,通路の幅を \(W\) とします。
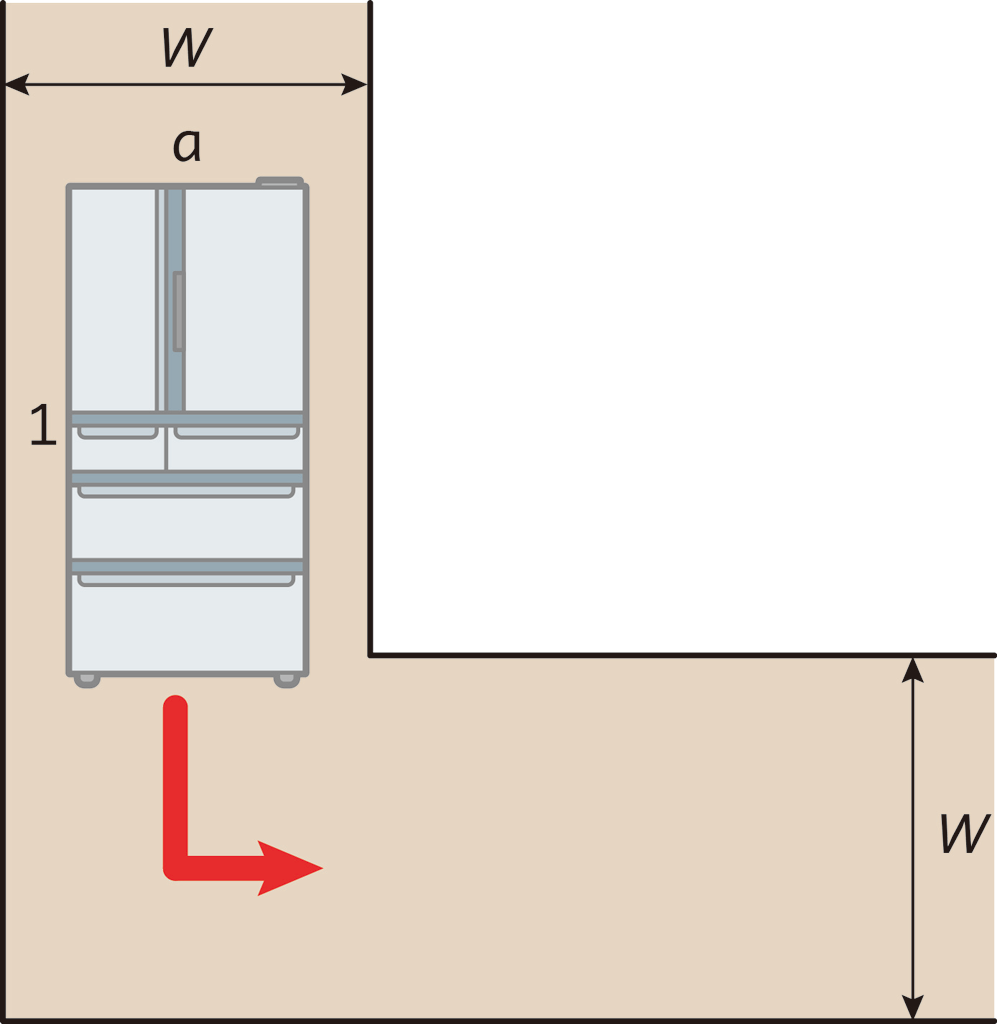
\(W\) が1より大きかったら,(実際はこういう運び方はしないでしょうけど)楽に運搬できます。
ですから,以後,\(0 \lt W \lt 1\) とします。
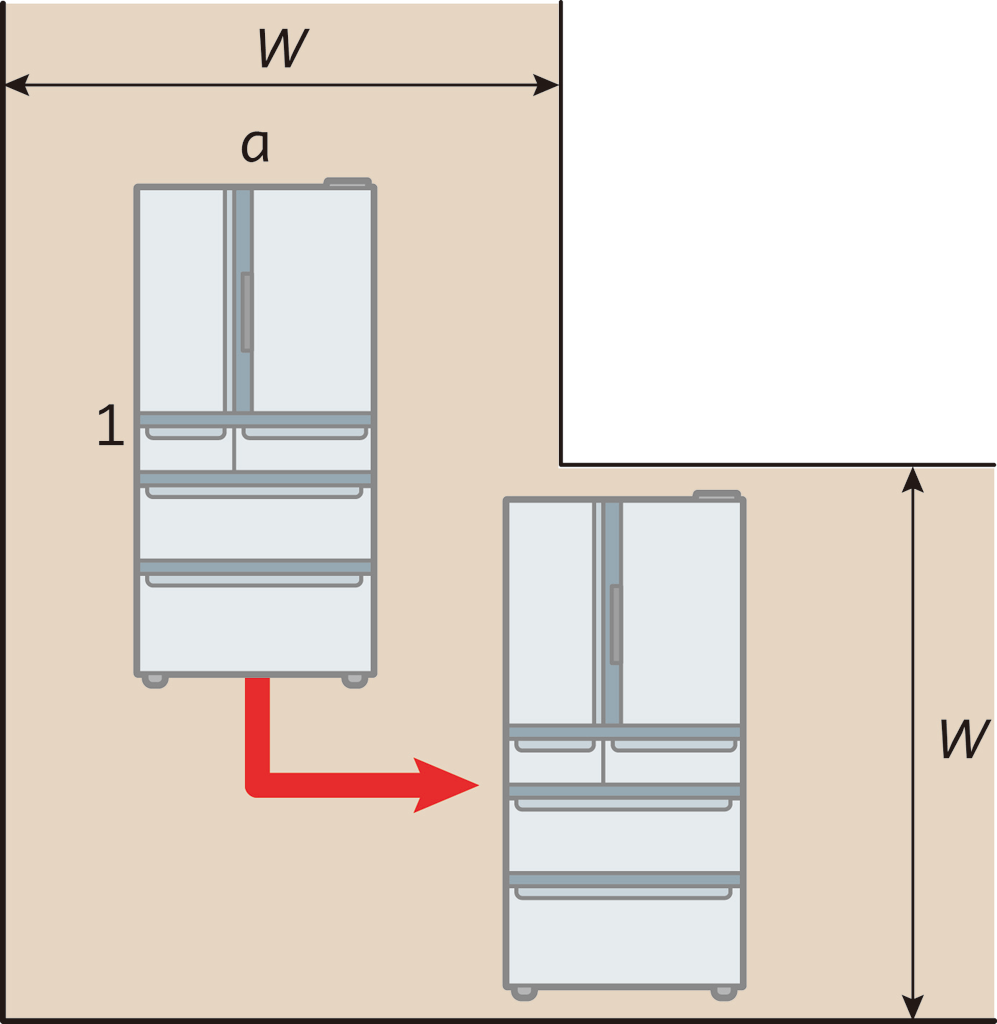
【疑問】\(0 \lt W \lt 1\),\(0 \lt a \leqq 1\) とします。このとき,幅 \( W\) のL字通路を通過できる長方形物体の短辺の長さ \(a\) の最大値はどのくらいになるでしょうか。あるいは,L字通路を縦横比が \(1\text{:}a\) の長方形が通過できるために必要な幅 \( W\) の最小値はどのくらいになるでしょうか,と聞いてもよいです。
すぐにはわかりませんね。もっと問題を簡単にしてみましょう。そのために長方形でない別の荷物の運搬を考えます。
黒板や絵画,あるいは大きなガラス板などは,面を水平に持って運ぶとたわんで破損する恐れがあるので,縦にして運ぶでしょう。

これらは真上から見たら細長い長方形,つまり棒です。棒がL字通路を通過する方法を考えることになります。
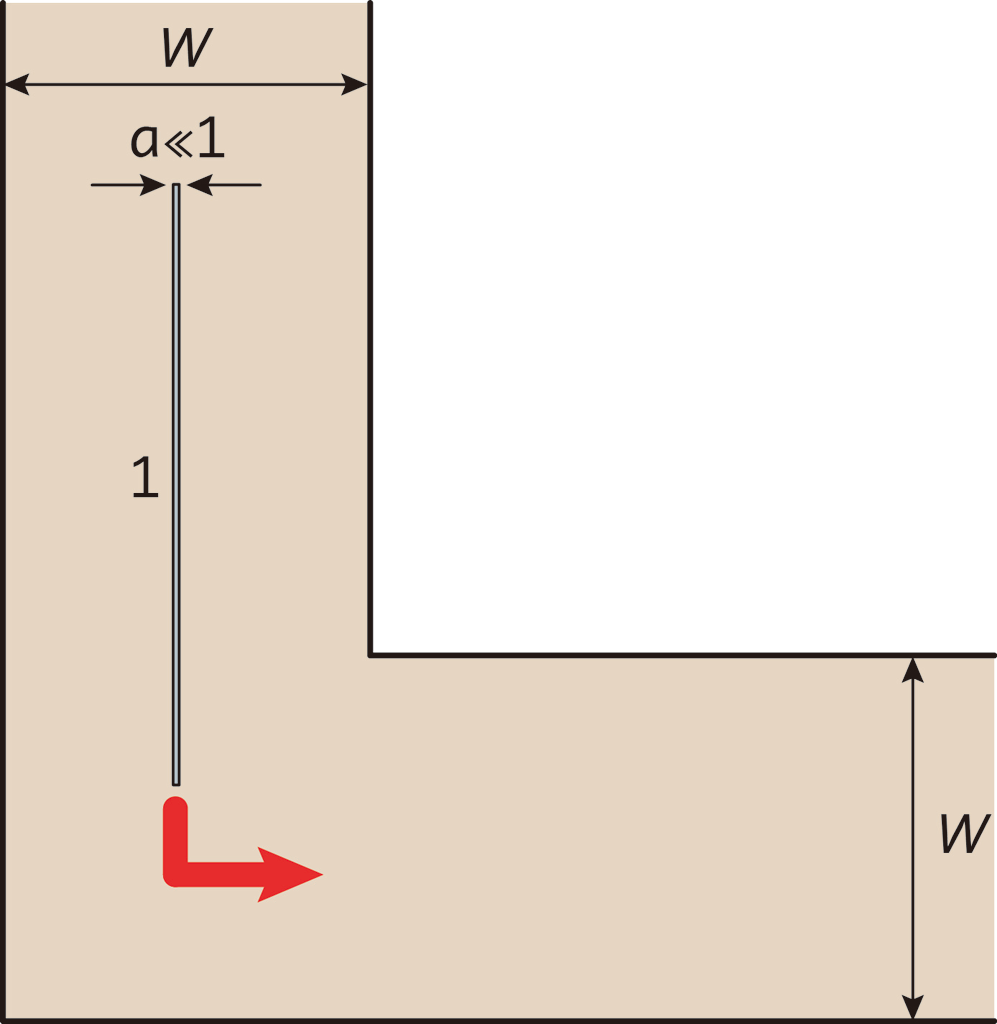
ただ,いくら \(a\) の値が小さくても,長方形は長方形なので,【疑問】の問題が簡単になったわけではありません。
そこで,数学的に問題を簡単にして,\(a=0\) にした長さ1の線分の移動を考えます。
【注意】本当の線分は見えませんので,図に表すときには幅のある棒を描くことになりますが,それを幅のない線分と想像します。このような抽象的思考が数学では重要であり,これが数学の強みです。
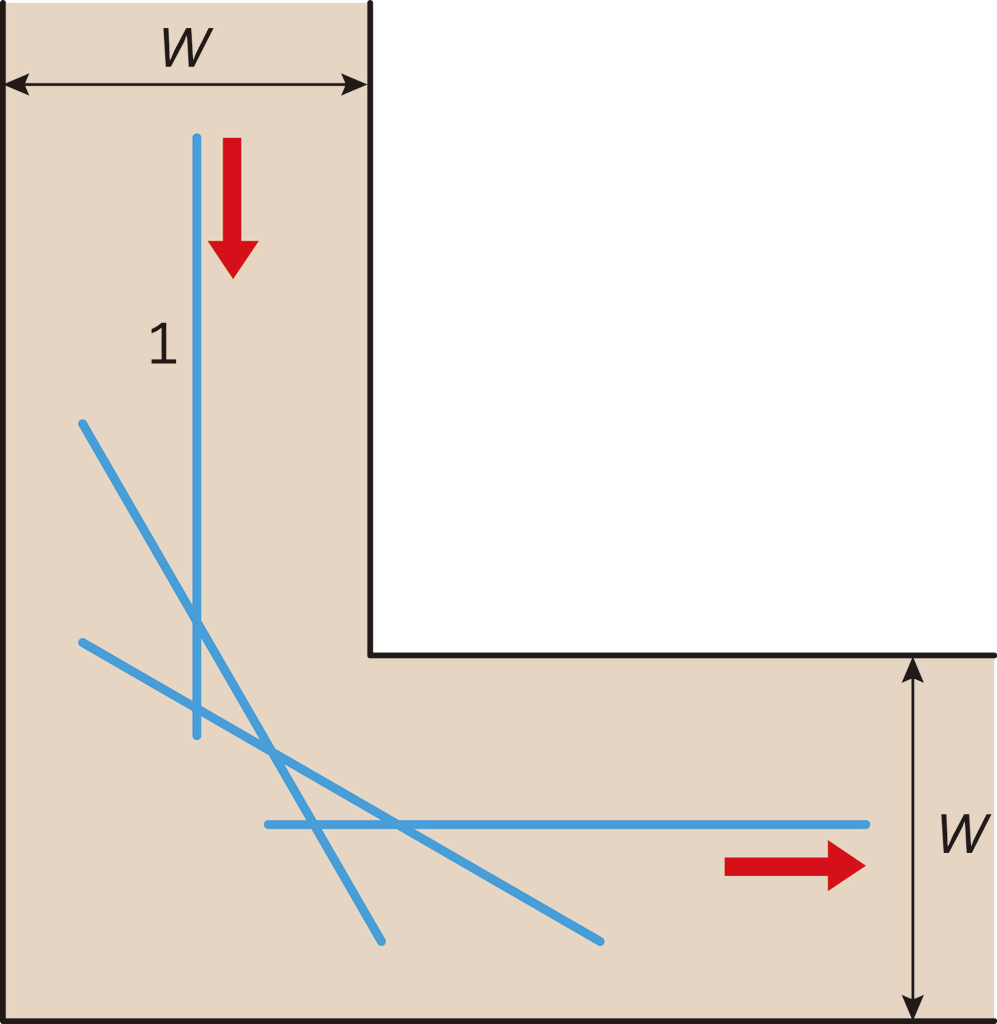
【疑問の簡単化】L字通路を長さ1の棒が通過できるために必要な幅 \(W\) の最小値はどのくらいになるでしょうか。
【簡単化した疑問の回答】下図において,L字通路の左の壁を \(y\) 軸,下の壁を \(x\) 軸,L字の左下の角を原点とします。長さ1の棒を両軸にもぶつからず,L字通路の内側の角「点 \( \text{A}\)」にもぶつからないように動かすために必要な条件を探します。
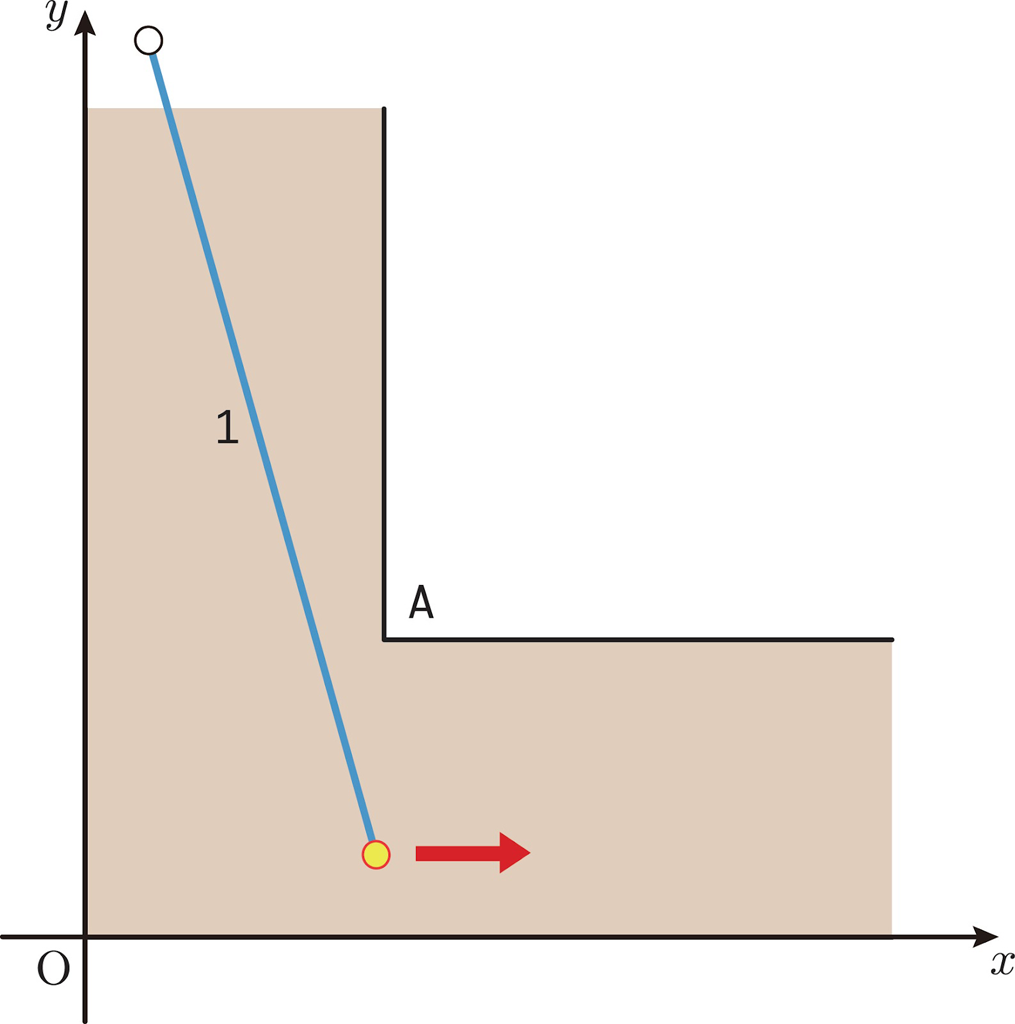
棒の上端を白丸,下端を黄丸としたとき,黄丸を赤矢印の方向に移動させると,棒は点 \( \text{A}\) や \(y\) 軸の壁にぶつかります。ですから,黄丸は通路のなるべく下側を移動させた方が,棒は点 \( \text{A}\) から離れます。
棒を点 \( \text{A}\) からなるべく遠ざけて動かすために,黄丸を原点にして,棒を \(y\) 軸上においた状態を初期状態とします。そして,白丸を \(y\) 軸上に,黄丸を \(x\) 軸上においたまま,赤の矢印,ピンクの矢印の順に,丸がそれぞれの軸上をすべるように動かすとよいでしょう。
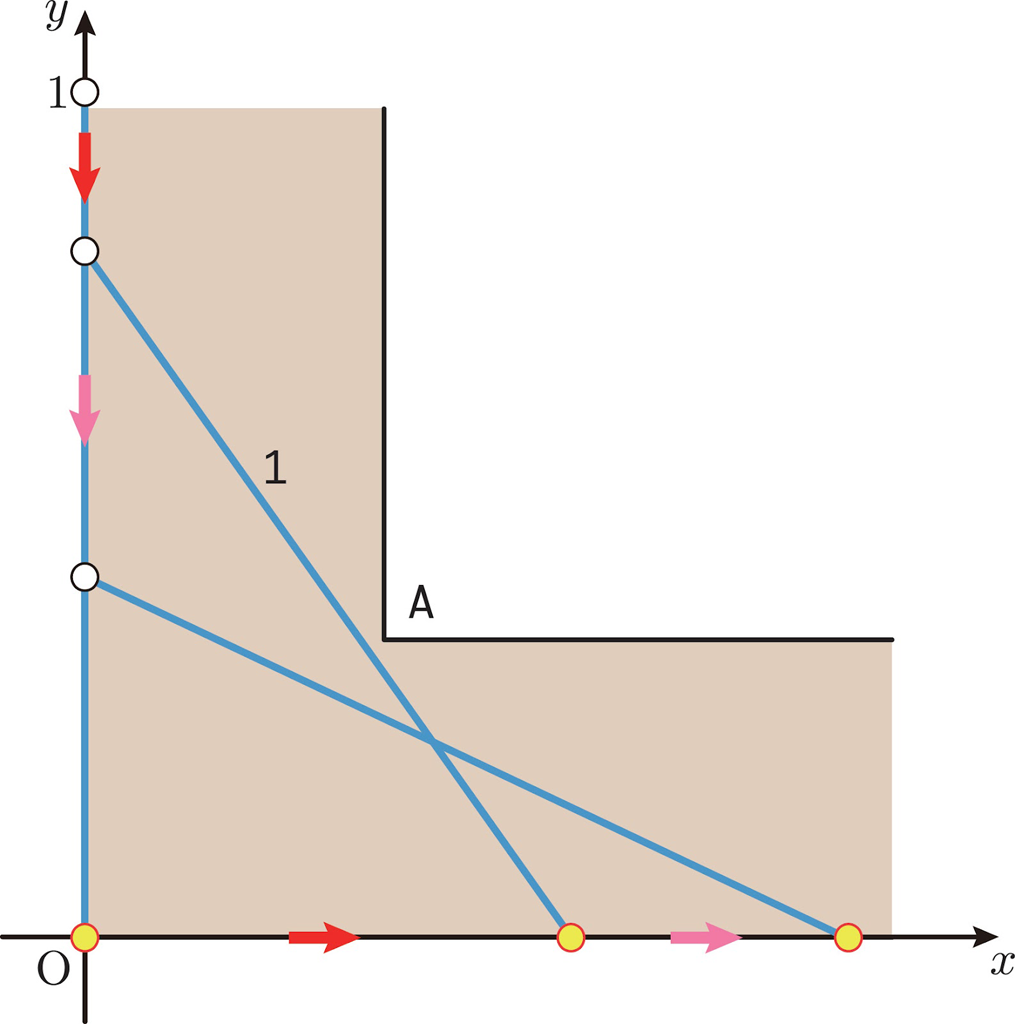
棒の軌跡を定量的に知るために,下図のように棒と \(x\) 軸のなす角度を \(x\) とします。このとき,棒の \(y\) 軸上の端(白丸)の \(y\) 座標は \(\sin t\) となり,\(x\) 軸上の端(黄丸)の \(x\) 座標は \(\cos t\) となります。\(t\) は \(\frac{\pi}{2}(90^\circ)\) から \(0(0^\circ)\) まで動きます。
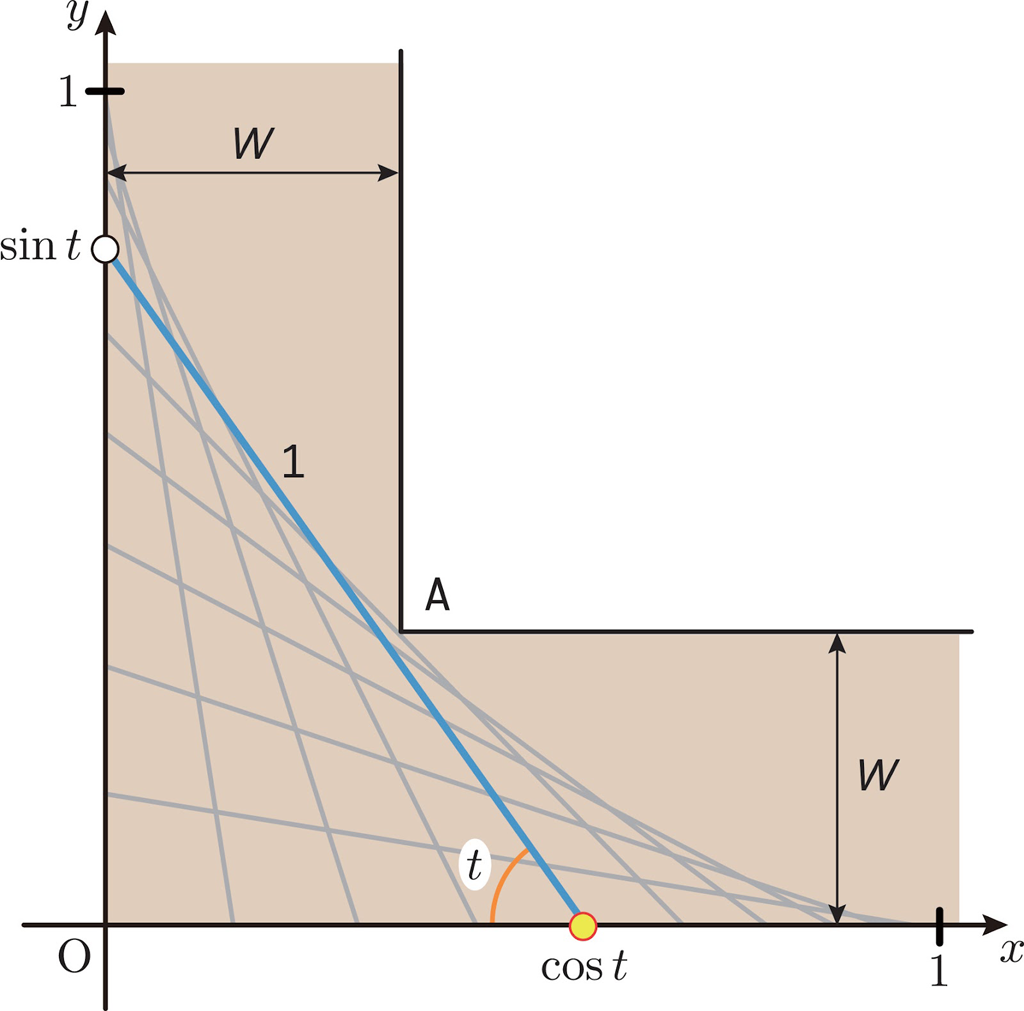
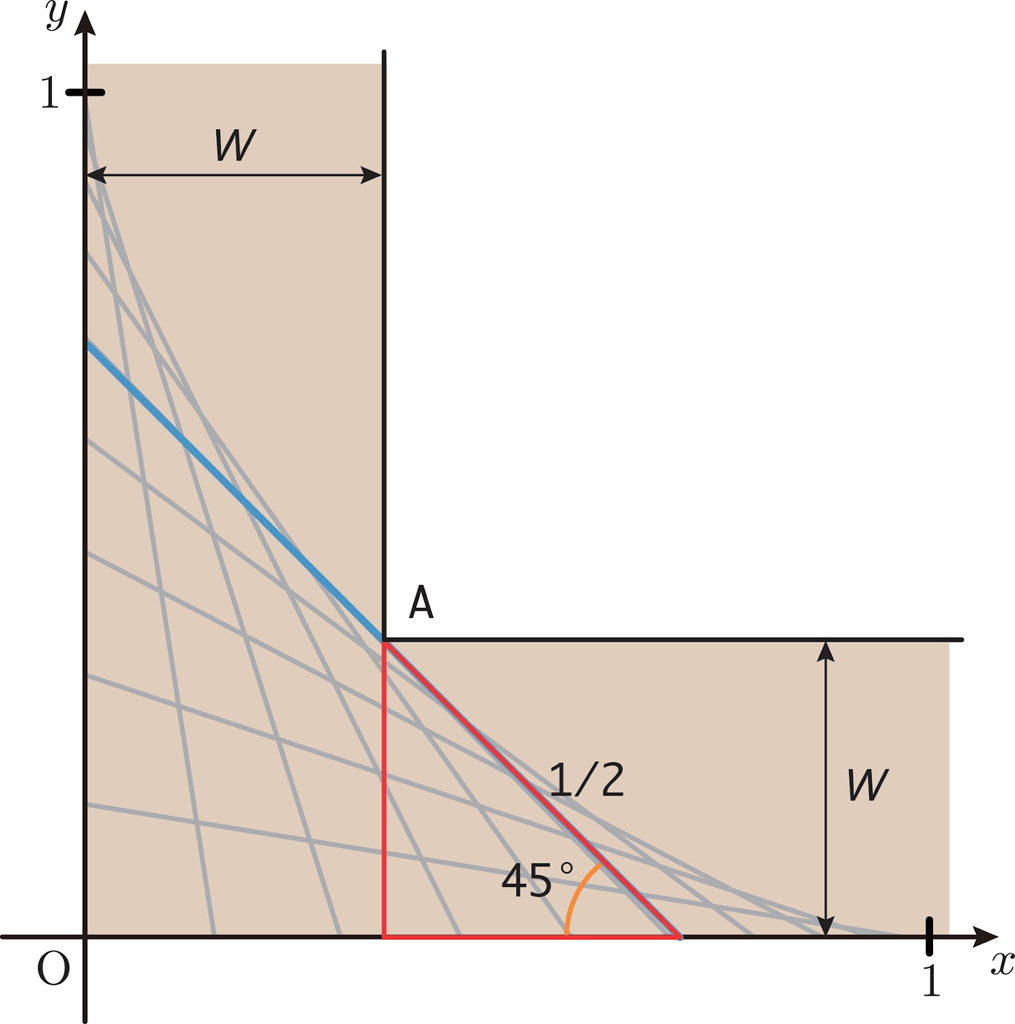
点 \( \text{A}\) の方向 \((1, 1)\) にもっとも棒が突き出るのは,\(45^\circ (t=\frac{\pi}{4})\) のときです。このとき,棒が点 \( \text{A}\) に接するとします。下図の赤い直角二等辺三角形の辺の長さから,対応する \( W\) の大きさは,\(W=\frac{\sqrt{2}}{4}\) になることがわかります。これが求める最小値です。
【注意】正確には,\(\frac{\sqrt{2}}{4}\) は棒が壁に接しないでL字通路を通過できる \( W\) の下限です。\( W\) がほんの少しでも \(\frac{\sqrt{2}}{4}\) より大きければ,棒は壁に接しません。ですから,\(W \gt \frac{\sqrt{2}}{4}\) が棒が壁に接しないための条件で,この条件を満たす \( W\) の最小値はないですが,下限として \(\frac{\sqrt{2}}{4}\) が得られました。
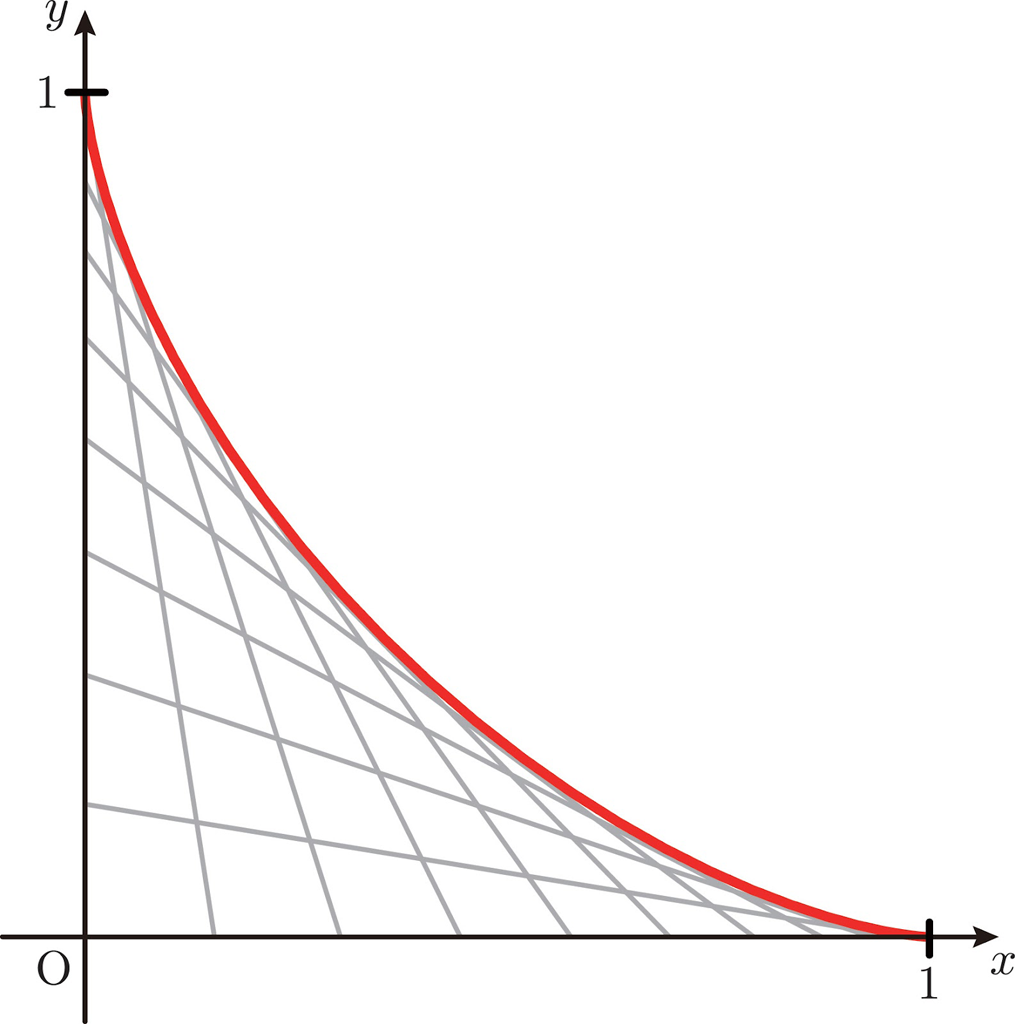
【寄り道:包絡線】長さ1の線分が通過する領域の境界で,軸を除いた曲線の部分は下図の赤い曲線になります。このように直線族(一般には曲線族)に対して,曲線 \(E\) が包絡線(envelope)であるとは,曲線 \(E\) 上のどの点も曲線族に属するある曲線上にあり,かつその点において,\(E\) とその曲線は共通接線をもち,しかも \(E\) 自身はその曲線族に属さないことをいいます。
包絡線を求める計算式から,この赤い曲線は \((\cos^3 t,\sin^3 t)\) とパラメータ表示されることがわかります。
この曲線は,\(t\) を \(0(0^\circ)\) から \(2{\pi}(360^\circ)\) まで動かすと下図のようになります。これはアステロイド(astroid)です。つまり,長さ1の棒の直線族の包絡線はアステロイドの一部であったことがわかりました。
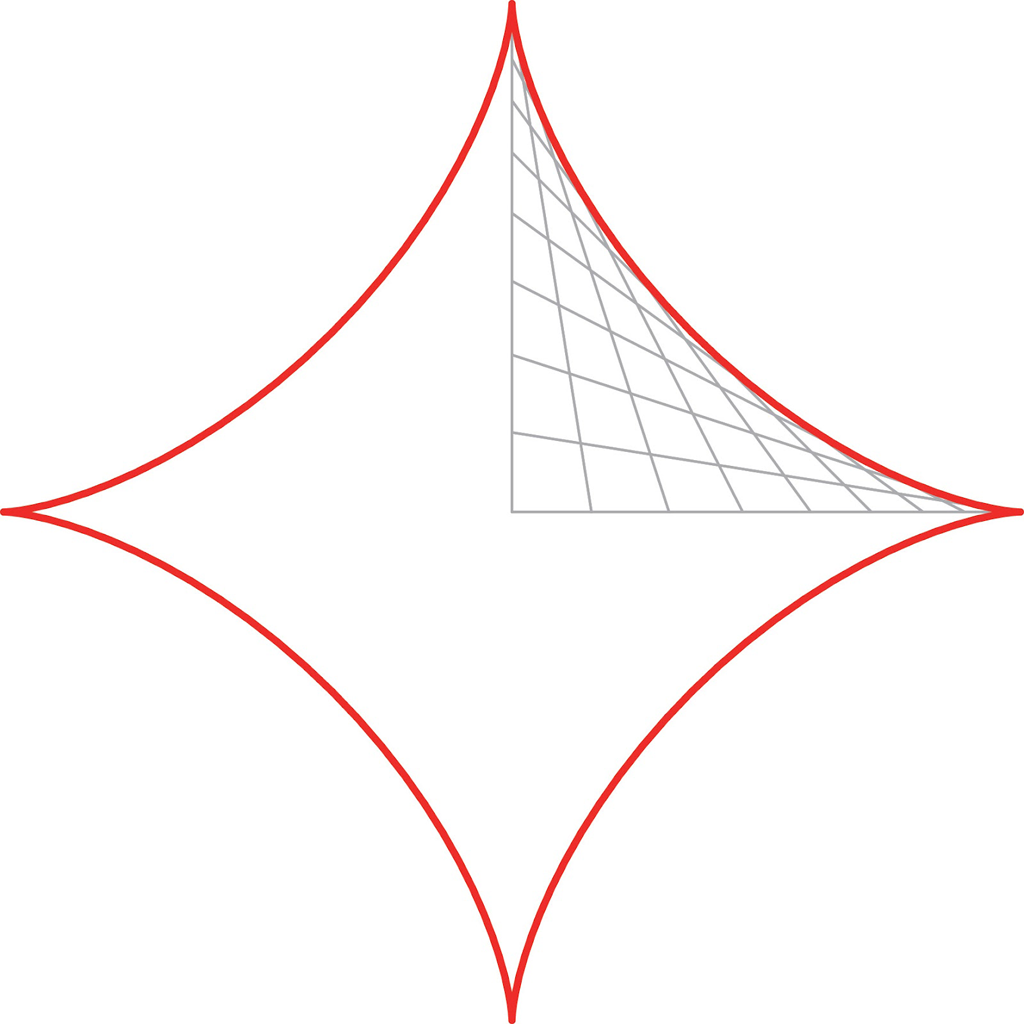
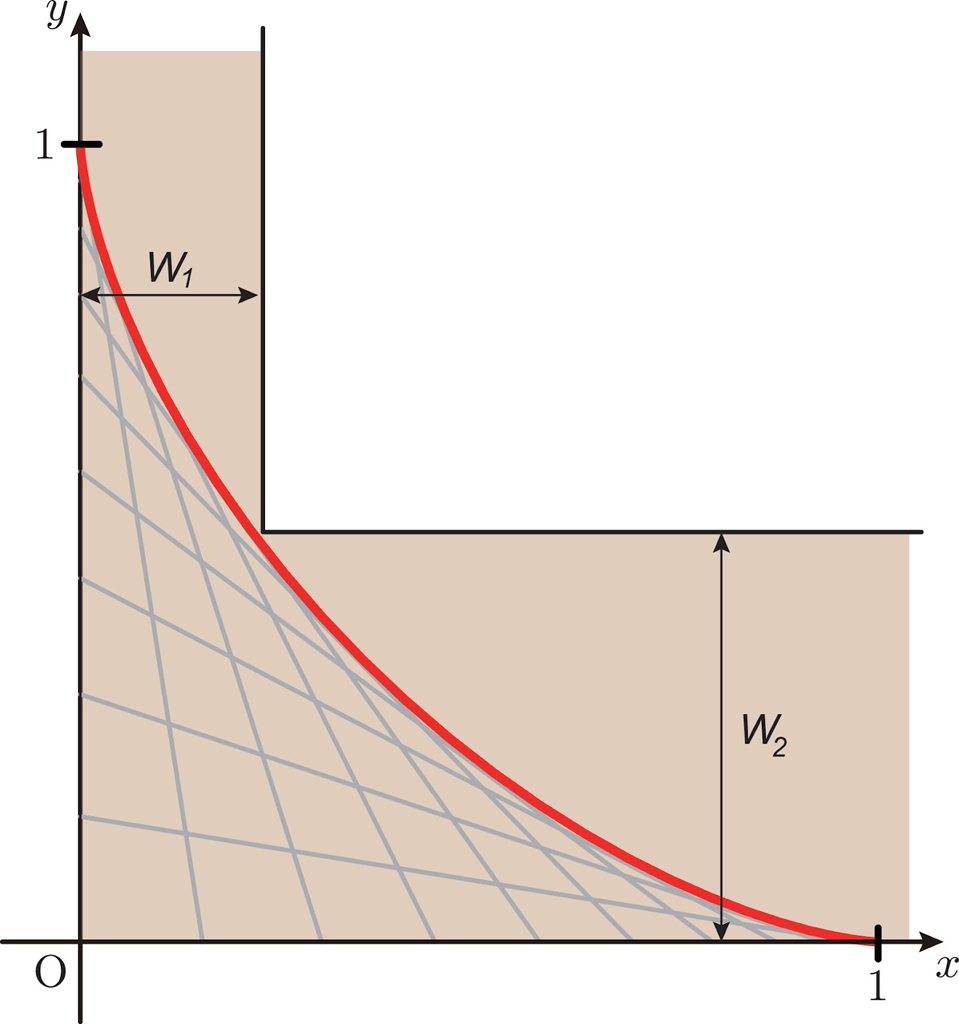
L字通路の幅が等しかったですが,下図のように狭い通路と広い通路を繋ぐL字通路であったとしても,このアステロイドにぶつからないようなL字通路であれば,棒は壁にぶつからず通過できることがわかります。
(後編では,いよいよ長方形の場合について考えます。)
※「つい考えてしまう数学」の記事一覧はこちら
1970年東京生まれ。早稲田大学理工学部数学科卒業。東京大学大学院数理科学研究科数理科学専攻博士課程修了。現在,明治大学理工学部数学科専任教授。博士(数理科学)。専門は応用数理,特に界面現象の数理解析。実験を採り入れた数学の講義で定評がある。
| 著書: | 『実験数学読本』①・②・③ (日本評論社),『次元解析入門』,『界面現象と曲線の微積分』,『動く曲線の数値計算』(以上共立出版),『大学数学の教則』(ちくま学芸文庫),『公式は覚えないといけないの?』(ちくまプリマー新書),他。 |
その他のコンテンツ
