特集記事（高校）

　前回は温度変化，特に過去のデータにもとづいた気温の変化について考察しました。今回も温度変化の話題ですが，未来の温度，あるいは過去の計測していない温度を推測することを考えます。

　下図は2025年7月1日の東京都（地点：東京）の0:10から24:00までの10分ごと144個の気温データのグラフです。

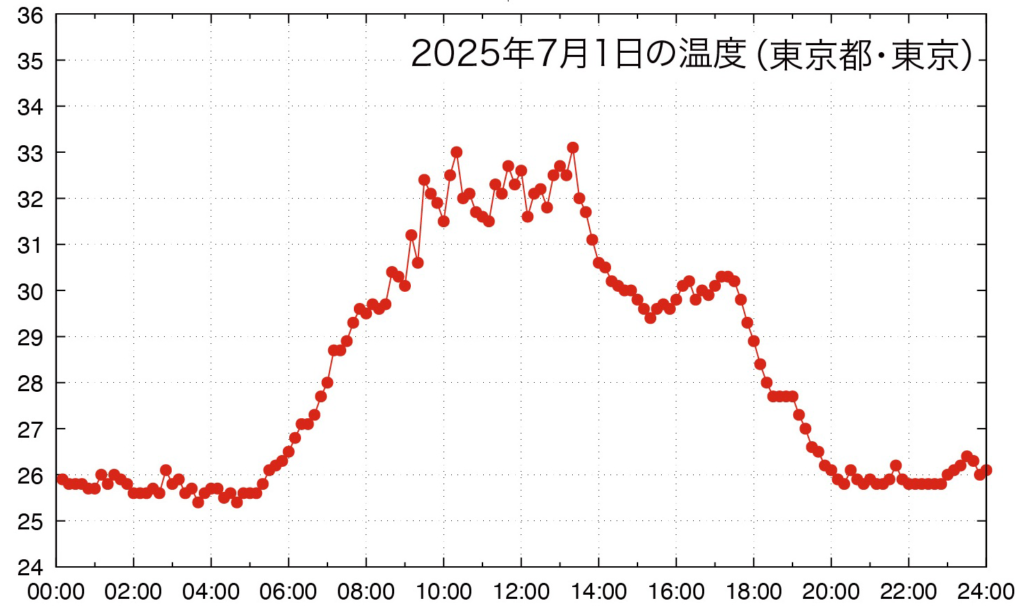
　次のように零時からの経過時間に10分おきに順次番号を付けます。

\( t_\text{1} = 10\text{min} \),　\( t_\text{2} = 20\text{min} \),　\(\cdots\),　\( t_\text{144} = 1440\text{min} \)

　つまり，経過時間 \(t_\text{n}\) は計測時刻に他なりません。そして，時刻 \(t_\text{n}\) における気温を \(T_\text{n}\) とします。だから，上のグラフにおいて，左から \({n}\) 番目の●の座標は \((t_\text{n}, T_\text{n})\) ということになります。ここで，\(t\) はtime（時間），\(T\) はtemperature（気温）のぞれぞれ頭文字です。

　例えば，\( t_\text{80} = 800\text{min} \)，つまり昼の13：20に最高気温 \( T_\text{80} = 33.1\) ℃を記録しています。一方，最低気温は25.4℃で，\( t_\text{22} = 220\text{min} \)（3：40）と \( t_\text{28} = 280\text{min} \)（4：40）の2回記録しています。

　一般に，過去の気温がわかっていても，明日の時刻 \(t_\text{n}\) における気温 \(T_\text{n}\) は予想の範囲でしかわかりません。ある場所，ある時刻での気温を決める要因は，太陽だけではなく，風や地熱など周囲の状況がすべて関わってきます。空間は地球全体で繋がっていますから，究極には気温は地球全体の状況によって決定されるものといえます。だから，現時点での気温 \(T_\text{n}\) がわかっていたとしても，10分後の気温 \(T_\text{n+1}\) を正確に予測することは難しいでしょう。だから天気予報は難しいのです。

　とはいえ，例えば地球の裏側の気候状況が10分の間に影響するとは考えにくいですから，10分間の気温の変化に影響する範囲はかなり限定的になるはずです。それでも，空が急に厚い雲におおわれたら気温に大きく影響するので，やはり気温の予測は難しいです。

　そこで，温度 \(T_\text{n}\) から \(T_\text{n+1}\) を予測できるように，状況を限定して考えてみます。

【疑問】湯飲みに入ったお湯の温度について考えます。下図において，初期時刻 \(t_\text{0}\) のお湯の温度を \(T_\text{0}\)（●），室温を \(T_{a}\) とし，一定とします。\(a\) はatmosphere（環境）の頭文字の気持ちです。通常は，室温よりお湯の温度が高いですから，ほうっておくと，お湯はだんだんと冷めていきます。各丸●○●は，一定の時間間隔で計測したときのお湯の温度です。同じ色の丸を繋いだ曲線を冷却曲線と呼びます。想定される冷却曲線は，3つの曲線のうちどれになるでしょうか。ただし，この曲線はイメージ図です。

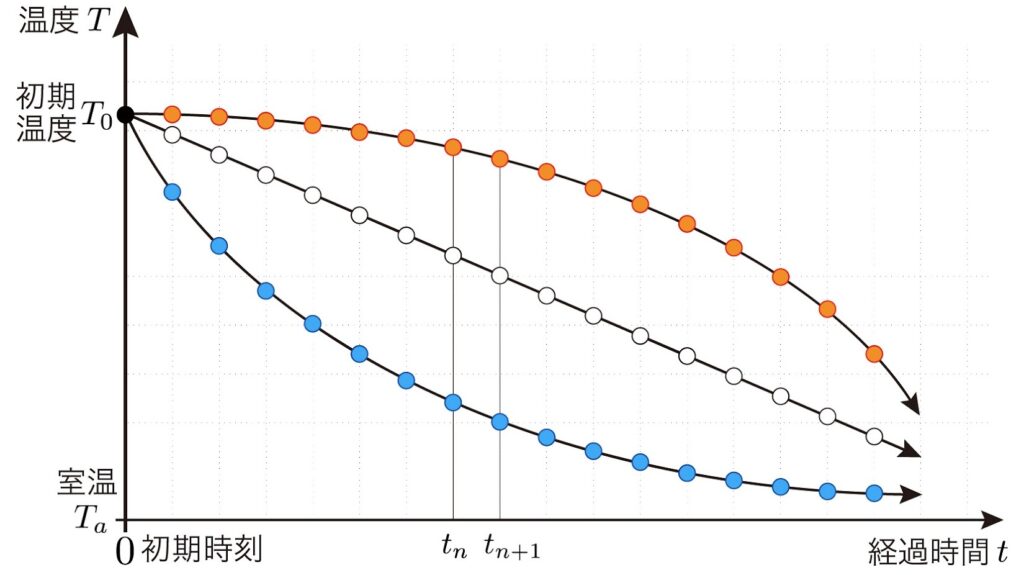
【答え】上図から観察できることは，●を繋いだ上に凸な曲線と○を繋いだ直線は，もっと時間が経つと，横軸にぶつかるでしょう。そうすると，横軸とぶつかった後，お湯の温度が室温よりもさらに下がるとは考えにくいので，ぶつかった瞬間から室温と同じ温度になるでしょう。一方，●を繋いだ下に凸な曲線は，だんだんと室温 \(T_\text{α}\) に漸近しています。こう考えると，●を繋いだ下に凸な曲線が冷却曲線といえそうです。

　下に凸な曲線の特徴は，一定の時間間隔における温度の下がり方が，温度が室温よりもだいぶ高いとその分急激に低下していて，室温との差があまりなくなってくると下がり方がゆるやかになっています。

　一般に，「温度の下がり方は，周囲の温度との差に比例する」という法則をニュートンの冷却の法則といいます。

　初期時刻 \(t_\text{0} = 0\) におけるお湯の温度 \(T_\text{0}\) が，その後どのように変化するのか，一定の時間間隔 \(τ\)（タウ）で，お湯の温度を計測したとします。

\(t_\text{1} = τ\),　\(t_\text{2} = 2τ\),　\(\cdots\),　\(t_\text{n} = nτ\)

　ここで，ギリシャ文字の \(τ\) は英語の \(t\) に相当するので，time（時間）に関連した文字として使いました。実験的には，\(τ = 20\text{s}\) や \(τ = 1\text{min}\) くらいを想定しています。経過時間 \(t_\text{n}\) から \(t_\text{n+1}\) の \(τ\) 時間の間に，お湯の温度は \(T_\text{n}\) から \(T_\text{n+1}\) へと変化します。その温度変化率は，

\( \cfrac{T_{n+1} – T_n}{τ} \)

です。下図は点 \((t_n, T_n)\) と点 \((t_{n+1}, T_{n+1})\) を結んだ線分の図です。上の温度変化率は下図の線分の傾きに相当します。

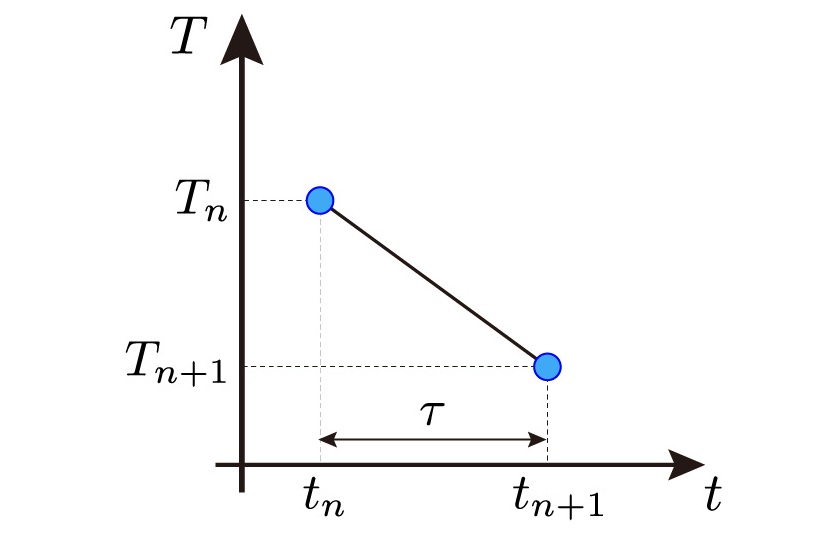
　上で紹介した2025年7月1日の気温のように，たとえ \(τ\) が小さくても，\(T_n\) から \(T_{n+1}\) を正確に予測するのは難しかったのですが，室内のお湯の温度ならば，その予測にニュートンの冷却の法則を適用しても問題ないことが実験的にわかっています。ニュートンの冷却の法則とは，上の温度変化率が，お湯の温度 \(T_n\) と周囲の室温 \(T_a\) との温度差に比例する，というものでした。これを式で表しましょう。比例定数を \(k > 0\) とします。

\( \cfrac{T_{n+1} – T_n}{τ} = -k(T_n – T_a) \)

　比例定数 \(k\) の値は湯飲みの材質などに依存して定まる正定数です。この式から，お湯の温度 \(T_n\) と室温 \(T_a\) の差が大きいとそれだけ温度変化率が大きくなって，逆に小さいと変化率も小さくなることがわかります。極端な場合，お湯の温度が室温と同じで \(T_n = T_a\) だったら，その後温度変化はおきません。

　上の式を書き換えると，

\(T_{n+1} = T_n – k(T_n – T_a)τ\)　\(\cdots\)(1)

となります。 時刻 \(t_n\) における温度 \(T_n\) がわかれば，比例定数 \(k\) と室温 \(T_a\) はわかっているので，時間間隔 \(τ\) を与えれば，上式の右辺の値が決まります。よって，時刻 \(t_{n+1}\) の温度 \(T_{n+1}\) が計測しないでも算出されます。

【疑問】初期時刻 \(t_0\) における温度 \(T_0\) がわかれば，適当な時刻 \(t_n\) における温度 \(T_n\) がわかるでしょうか。

　(1)式が漸化式だと看破した人は，きっとこの疑問に答えられるでしょう。回答のポイントは，温度の基準を \(T_a\) にすることです。つまり，室温との温度差が重要な値なので， \(T_n – T_a\) から \(T_{n+1} – T_a\) にどう変化するのかをみます。

【答：未来の温度】(1)式の両辺から \(T_a\) を引いて整理すると，

\(T_{n+1} – T_a = (1 – {kτ})(T_n – T_a)\)　\(\cdots\)(2)

となります。\(k\) は湯飲みの材質などで決まっている正定数なので，\(τ\) を十分小さくとって，\(0<{kτ}<1\) となるようにしておけば，(2)式から，お湯の温度と室温の温度差が \(τ\) 時間経過するごとに \(1-{kτ}\) 倍になることがわかります。したがって，
\(2τ\) 時間経過したら \((1-{kτ})^2\) 倍
\(3τ\) 時間経過したら \((1-{kτ})^3\) 倍
……
のように続けられます。よって，初期時刻から \(t_n = {nτ}\) 時間経過したら \((1-{kτ})^n\) 倍になるのだから，

\(T_n – T_a = (1 – {kτ})^n(T_0 – T_a)\)

となって，これより，初期温度 \(T_0\) がわかれば，\(n = 1,2,3,\) …に対して，\(t_n\) 時間後の未来の温度 \(T_n\) が

\(T_n = (1 – {kτ})^n(T_0 – T_a) + T_a\)　\(\cdots\)(3)

からわかります。
　最後に(3)式を次のように\(T_0 =\) …の形に変形します。

\(T_0 = (T_n – T_a)(1 – {kτ})^{-n} + T_a\)　\(\cdots\)(4)

【疑問】この式の意味はどう捉えられるでしょうか。

【答：過去の温度】現在の時刻を \(t_n\) とします。このとき，(4)式は \(t_n\) 時間前の時刻 \(t_0\) における温度を表している式といえます。

　つまり，過去に温度を計測しなかったとしても，現在の温度がわかれば，遡って過去の温度が推測できるということになります。この考えを使って死亡推定時刻を求めることができますが，それについてはまた今度。

■ ニュートンの贈り物

　ニュートンは，あの有名なアイザック・ニュートンその人のことである（Sir Isaac Newton，1643.1.4－1727.3.31（グレゴリオ暦），イングランド）。しばしばニュートンはガリレオが死んだ年に生まれたといわれるが，ユリウス暦とグレゴリオ暦を都合よく混同したとしても実際の生没年にはずれがある。しかし，ガリレオが没したのは1642年1月8日で，ニュートン誕生は翌年の1月4日だから日にちが非常に近いし，なによりニュートンはガリレオの残した業績をさらに昇華させたといってよいから，ガリレオが没し，ニュートンが誕生したという言い方をしても，二人から多大な恩恵を受けている後世の人からすれば楽しい物語である。

　ニュートンの名を冠した「もの」は沢山ある。例えば，Wikipediaのこのページ（※外部サイト）を参照されたい。1701年に発表されたニュートンの冷却の法則（Newton’s law of cooling）は，ニュートンの膨大な業績の一つのアクセサリーに過ぎないが，熱の伝導に関する初めての法則であるし，現在でも例えば温度変化に関する偏微分方程式の熱損失の項として使われているように全く色あせていない。ニュートンの冷却の法則の約100年後に登場するフーリエによる熱伝導の法則，あるいはフーリエの法則（Jean Baptiste Joseph Fourier，1768－1830）の離散版と捉えることもできる。

※「つい考えてしまう数学」の記事一覧はこちら