今年の夏も暑い日が続いています。熱中症には十分気をつけたいですね。
熱中症のリスクを測るものとして「暑さ指数(WBGT)※」があります。実際に暑さ指数が上がると熱中症により救急搬送される人数も増えますが,両者にはどのような関係があるのでしょうか。
※気温,湿度,日射・輻射などの熱環境を組み合わせて算出される熱中症予防を目的とした指標
『数学B Advanced』では,WBGTと搬送者数の関係について,片対数グラフを用いて回帰分析をする課題を取り上げています。
今年の夏についても,同様に調べてみましょう。以下のWebサイトのデータを利用します。
① 熱中症予防情報サイト(環境省)… 全国各地のWBGTのデータ
② 総務省消防庁 熱中症情報 … 熱中症による救急搬送者数のデータ
東京の5月から7月までを例にとります。②では東京都の週ごとの搬送者数のデータが得られるため,これを日割りして1日あたりの搬送者数を \(y\)(人)とします。
次に,①から得た東京の各日のWBGTの最高値を週ごとに平均した値を \(x\)(℃)とし, \(x\) と \(y\) を対応させます。(データはこちら)
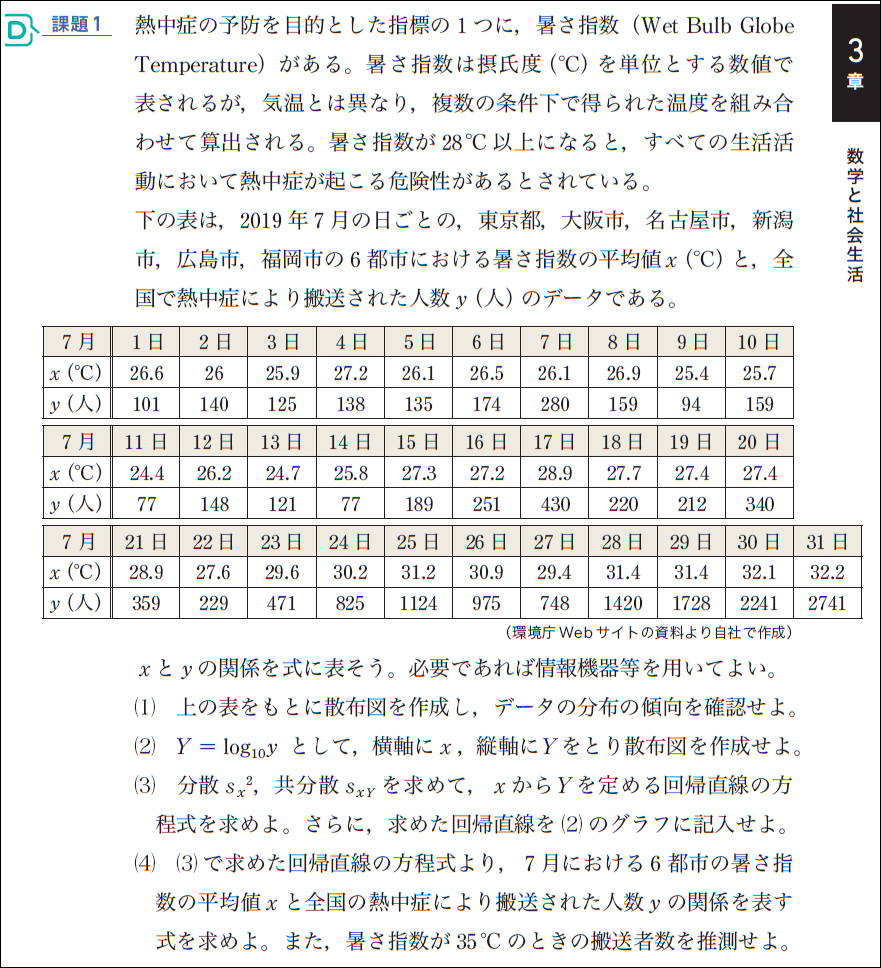
これを散布図に表すと,次のようになります。
WBGTの値が高くなると搬送者数が急に増加しており,指数関数的な関係にありそうなことが散布図から見てとれます。
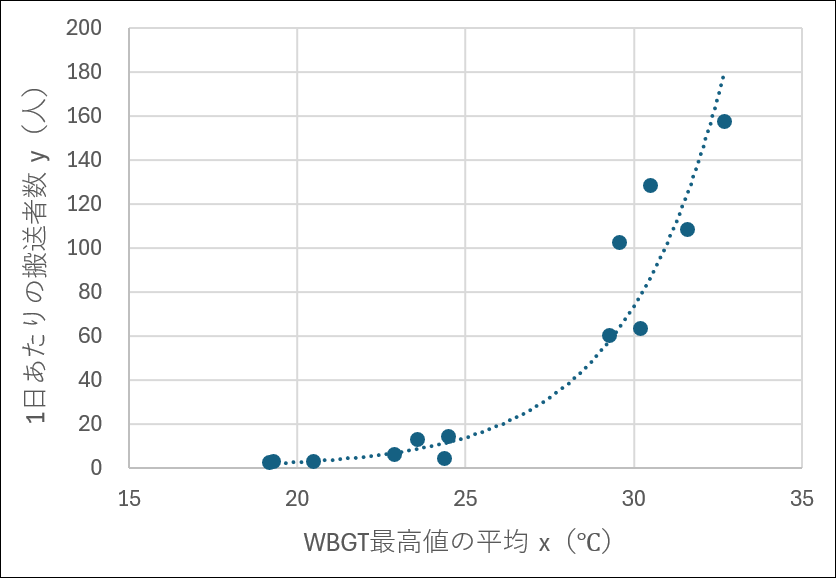
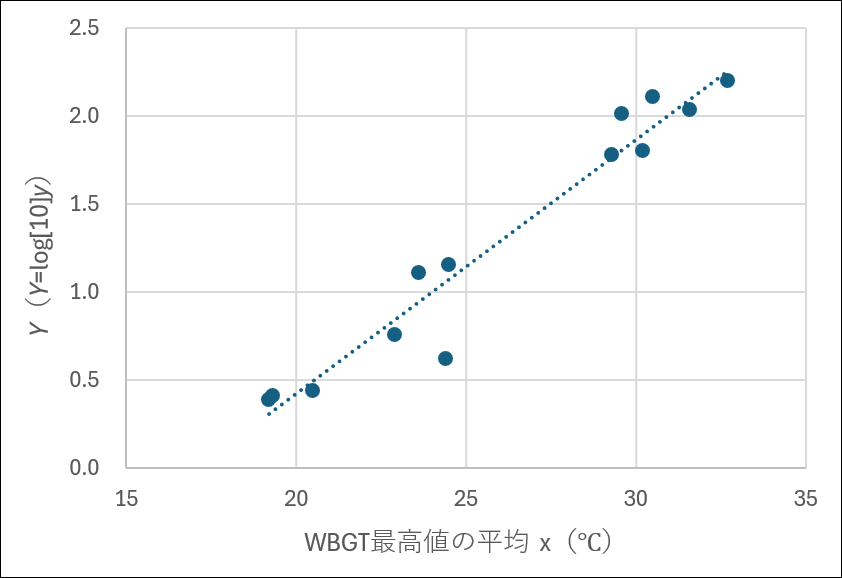
よって,散布図の縦軸にあたる搬送者数の常用対数をとった値を \(Y\text{(}Y=\log_{ 10 } y \text{)}\)とし,\(x\) と \(Y\) を対応させて片対数の散布図に表すと,次のようになります。(データはこちら)
先ほどの散布図に比べると,直線状に近い分布になりました。
計算すると,\(x\) の平均 \(\overline{ x }\) は \(26.0\),分散 \({s_{x}} ^{ 2 }\) は \(21.5\),\(Y\) の平均 \(\overline{Y}\) は \(1.292\), \(x\) と \(Y\) の共分散 \(s_{xY}\) は \(3.10\) より, \(x\) と \(Y\) の回帰直線の方程式は次のようになります。
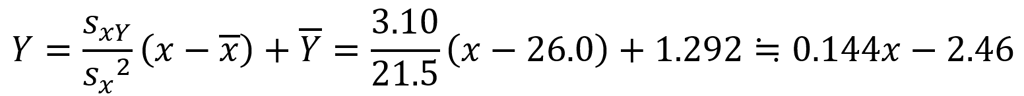
以上より, \(x\) と \(y\) の関係式は
\(\large{y=10^{0.144x-2.46}}\)
となり,暑さ指数が上がると搬送者数が急に増加する様子を式に表すことができました。
なお,暑さ指数では28以上31未満を「厳重警戒」,31以上を「危険」と区分しています。
このように実際のデータを用いて考察することで,熱中症のリスクに対する理解も深まります。ぜひ,お住まいの都道府県のデータで試してみてください。
その他のコンテンツ