特集記事（高校）

長崎大学 教授
中川 幸久 先生

第4回　講義

（第3回はこちら）

講義のねらい

【加法と減法】

　第1回講義から第3回講義までの講義は，角の分解を実際に算出する場合と連鎖探索法による場合を紹介し，その違いを比較して考察した。
　第4回講義では，角の合成や分解を，和や差の演算として捉え，一般的な加法，減法として論じることができないか，正接の加法定理に立ち戻り考察を深めてみた。
　正接をつくる直角の型の集合は，加法を定義すると群をなしていることが分かった。また， 逆演算の減法も可能になった。
　図形的な角の合成を代数的に演算できることが興味深い。

5.加法と減法

正接でつくる集合 \(S\)

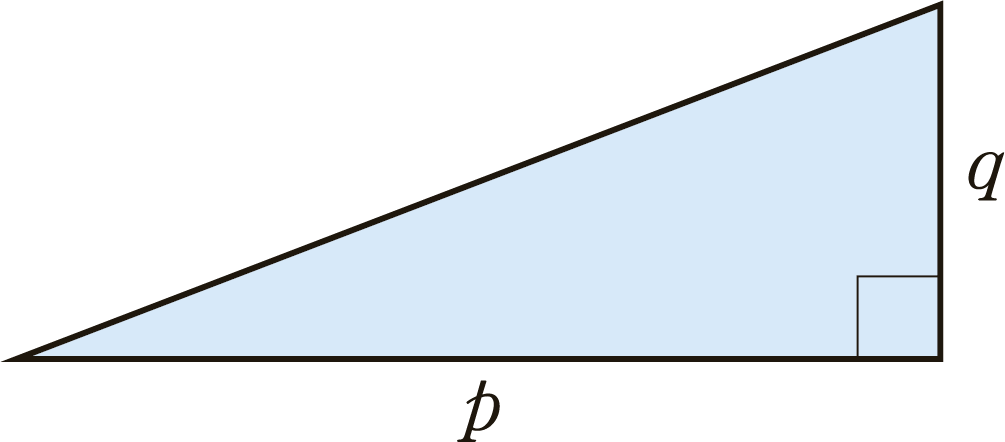
　底辺の長さを \(p\)，高さを \(q\) とする直角三角形ならば　　\(\tan\theta = \frac{q}{p}\)

　下の表のように分布し，\(\frac{1}{1}\)，\(\frac{2}{1}\)，\(\frac{1}{2}\)，\(\frac{3}{1}\)，\(\frac{2}{2}\)，\(\frac{1}{3}\)，\(\frac{4}{1}\)，\(\frac{3}{2}\)，…，\(\frac{q}{p}\)，…と斜めに読み込むと，有理数と同じ可付番集合の無限集合である。

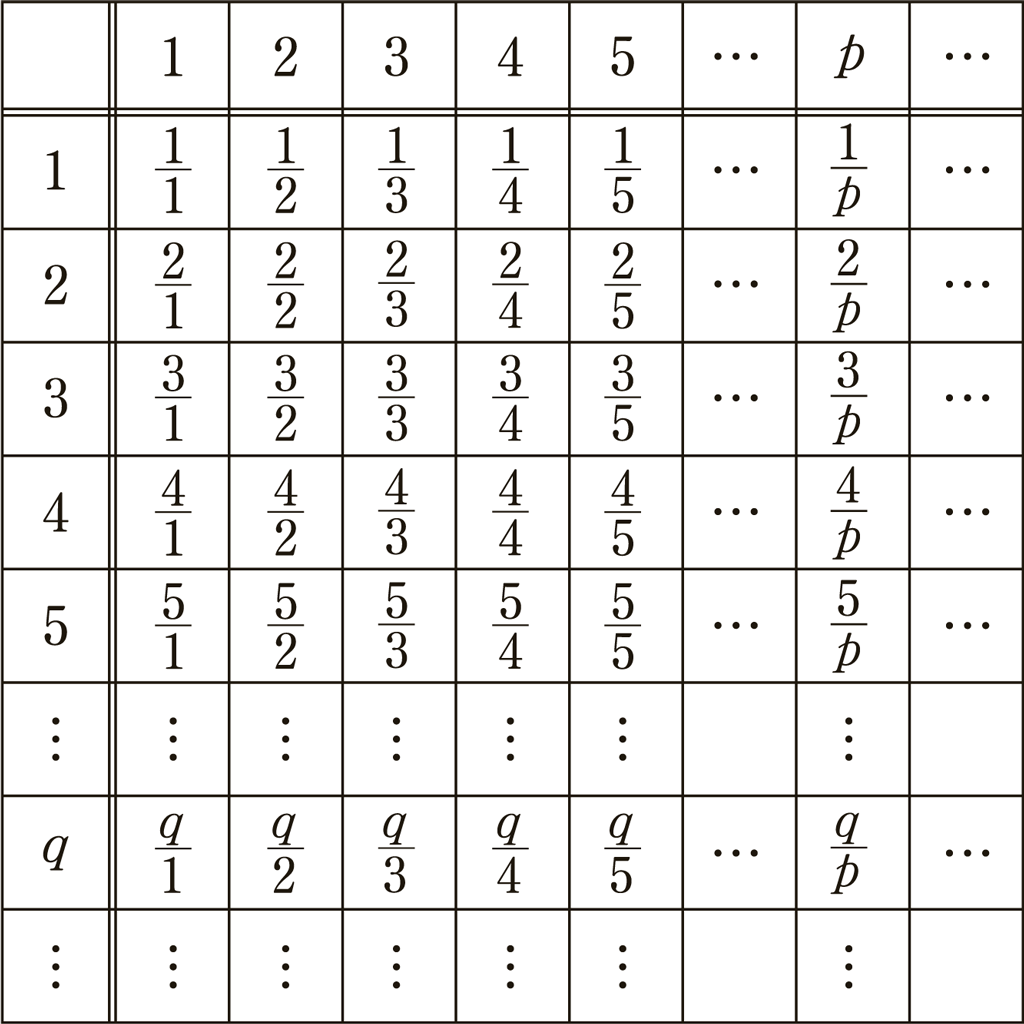
　正接が \(\frac{q}{p}\) となる角を \((p, q)\) で表す。

　4つの正の数 \(a, b, c, d\) に対して \(\tan\theta_1=\frac{b}{a},\ \tan\theta_2=\frac{d}{c}\) とすると

\(\tan(\theta_1+\theta_2)=\frac{\tan\theta_1+\tan\theta_2}{1-\tan\theta_1\tan\theta_2}=\dfrac{\frac{b}{a}+\frac{d}{c}}{1-\frac{b}{a}\cdot\frac{d}{c}}=\frac{bc+ad}{ac-bd}\)

　これは，\((ac-bd, bc+ad)\) に対応するので，和を \(\color{#ff0000}{(a, b)+(c, d)=(ac-bd, bc+ad)}\) と定義する。
　ただし，\(\color{#ff0000}{k \gt 0}\) に対して　\(\color{#ff0000}{(ka, kb)=(a, b)}\)

（例）\((3, 1)+(7, 1)=(3\cdot 7-1\cdot 1, 1\cdot 7+3\cdot 1)=(20, 10)=(2, 1)\)
（例）\((5, 1)+(8, 1)=(5\cdot 8-1\cdot 1, 1\cdot 8+5\cdot 1)=(39, 13)=(3, 1)\)

　連鎖探索法より確認する。
\((2, 1)=(3, 1)+(7, 1)\) として表せる。
\((3, 1)=(5, 1)+(8, 1)\) として表せる。

（1）\((3, 1)+(4, 3)=(3\cdot 4－1\cdot 3, 1\cdot 4+3\cdot 3)=(9, 13)\)
（2）\((5, 3)+(6, 5)=(5\cdot 6－3\cdot 5, 3\cdot 6+5\cdot 5)=(15, 43)\)
（3）\((4, 1)+(3, 2)=(4\cdot 3－1\cdot 2, 1\cdot 3+4\cdot 2)=(10, 11)\)
（4）\((2, 3)+(5, 2)=(2\cdot 5－3\cdot 2, 3\cdot 5+2\cdot 2)=(4, 19)\)

　\(ac-bd=0\) のときは，正接の値がないので，\((a, b)\) と \((c, d)\) を加えると直角になっている。
　\(ac-bd\lt 0\) のときは，正接が負になることから，\((a, b)\) と \((c, d)\) を加えると鈍角になっている。

（例）
（1）\((2, 3)+(3, 2)=(2\cdot 3-3\cdot 2, 3\cdot 3-2\cdot 2)=(0, 13)\)
　2つの角の和は直角である。
（2）\((2, 5)+(10, 4)=(2\cdot 10-5\cdot 4, 5\cdot 10+2\cdot 4)=(0, 58)\)
　2つの角の和は直角である。
（3）\((1, 3)+(2, 3)=(1\cdot 2-3\cdot 3, 3\cdot 2+1\cdot 3)=(-7, 9)\)
　2つの角の和は鈍角である。
（4）\((3, 5)+(4, 3)=(3\cdot 4-5\cdot 3, 5\cdot 4+3\cdot 3)=(-3, 29)\)
　2つの角の和は鈍角である。

　これから，正接を表す組 \((a, b)\) の \(a, b\) は，すべて整数として定義し，この集合を \(T\) とする。

　2組の角の和を \(\color{#ff0000}{(a, b)+(c, d)=(ac-bd, bc+ad)}\) として定義したように，差も同じように定義する。

【差の定義】

\(\tan(\theta_1-\theta_2)=\frac{\tan\theta_1-\tan\theta_2}{1+\tan\theta_1\tan\theta_2}=\dfrac{\frac{b}{a}-\frac{d}{c}}{1+\frac{b}{a}\cdot\frac{d}{c}}=\frac{bc-ad}{ac+bd}\)

　正接の加法定理より，差は \((ac+bd, bc-ad)\) に対応するので，2組の角の差を \(\color{#ff0000}{(a, b)-(c, d)=(ac+bd, bc-ad)}\) と定義する。

　例えば

(1) \((1, 1)-(3, 1)=(1\cdot 3+1\cdot 1, 1\cdot 3-1\cdot 1)=(4, 2)=(2, 1)\)
　逆に，\((2, 1)+(3, 1)=(2\cdot 3-1\cdot 1, 2\cdot 1+1\cdot 3)=(5, 5)=(1, 1)\) が成り立つ。
(2) \((5, 1)-(18, 1)=(5\cdot 18+1\cdot 1, 1\cdot 18-5\cdot 1)=(91, 13)=(7, 1)\)
　逆に，\((7, 1)+(18, 1)=(7\cdot 18-1\cdot 1, 7\cdot 1+1\cdot 18)=(125, 25)=(5, 1)\) が成り立つ。

\(\color{#ff0000}{(a, b)-(c, d)=(ac+bd, bc-ad)}\) より

\(\color{#ff0000}{(ac+bd, bc-ad)+(c, d)}\)
\(\color{#ff0000}{=((ac+bd)c-(bc-ad)d, (bc-ad)c+(ac+bd)d)}\)
\(\color{#ff0000}{=(ac^2+bcd-bcd+ad^2, bc^2-acd+acd+bd^2)}\)
\(\color{#ff0000}{=(ac^2+ad^2, bc^2+bd^2)}\)
\(\color{#ff0000}{=(a(c^2+d^2), b(c^2+d^2))}\)
\(\color{#ff0000}{=(a, b)}\)
が成り立つ。

　1つの例として，

\((4, 3)-(3, 4)=(4\cdot 3+3\cdot 4, 3\cdot 3-4\cdot 4)=(24, -7)\)

を考える。

　角 \((4, 3)\) が角 \((3, 4)\) より小さいので結果は負になる。
　図形的に捉えても，\((24, -7)\) は正接が負になっており，正負の符号は一致する。
\((24, -7)=-(24, 7)\) として扱えばよい。
　ここで，\((3, 4)-(4, 3)\) と \((4, 3)-(3, 4)\) を比較してみる。
\((3, 4)-(4, 3)=(3\cdot 4+4\cdot 3, 4\cdot 4-3\cdot 3)=(24, 7)\)　…①
\((4, 3)-(3, 4)=(24, -7)\)　…②
　①，②より，\((24, -7)=-(24, 7)\) と考えられる。 なお，角としては \((-24, -7)=(24, 7)\) であり，\(-(24, 7)\neq(-24, -7)\) であることを注意したい。

\(\color{#ff0000}{(a, b)+(c, d)=(ac-bd, bc+ad)}\) より
\((a, b)+(1, 0)=(a\cdot 1-b\cdot 0, b\cdot 1+a\cdot 0)=(a, b)\)
\((1, 0)+(a, b)=(1\cdot a-0\cdot b, 0\cdot a+1\cdot b)=(a, b)\)

【まとめ】演算の整理

　角をつくる \((a, b)\)，\((c, d)\) の \(a, b, c, d\) については，\(0\) や負の整数まで拡張し，その集合を \(T\) として演算を定義する。

\(\color{#ff0000}{(a, b)+(c, d)=(ac-bd, bc+ad)}\) より
（1）\((3, 1)+(4, 3)=(3\cdot4-1\cdot3, 1\cdot4+3\cdot3)=(9, 13)\)
（2）\((5, 2)+(6, 1)=(5\cdot6-2\cdot1, 2\cdot6+5\cdot1)=(28, 17)\)
（3）\((2, -1)+(3, 4)=(2\cdot3-(-1)\cdot4, (-1)\cdot3+2\cdot4)=(10, 5)=(2, 1)\)
（4）\((2, 7)+(3, -1)=(2\cdot3-7\cdot(-1), 7\cdot3+2\cdot(-1))=(13, 19)\)

\(\color{#ff0000}{(a, b)-(c, d)=(ac+bd, bc-ad)}\) より
（1）\((6, 5)-(3, 2)=(6\cdot 3+5\cdot 2, 5\cdot 3-6\cdot 2)=(28, 3)\)
（2）\((7, 3)-(2, 1)=(7\cdot 2+3\cdot 1, 3\cdot 2-7\cdot 1)=(17, -1)\)
（3）\((3, 4)-(5, 8)=(3\cdot 5+4\cdot 8, 4\cdot 5-3\cdot 8)=(47, -4)\)
（4）\((1, 1)-(2, -5)=(1\cdot 2+1\cdot (-5), 1\cdot 2-1\cdot (-5))=(-3, 7)\)

（資料4－①）

\(\color{#ff0000}{(a, b)+(c, d)=(ac-bd, bc+ad)}\) より
（算出1）\((1, 1)＝(2, 1)+(3, 1)\)
（右辺）\(=(6-1, 3+2)=(5, 5)=(1, 1)\)
（算出9）\((1, 1)=(2, 1)+(5, 1)+(9, 1)+(73, 1)\)
（右辺）\(=(10-1, 5+2)=(9, 1)=(73, 1)\)
\(\hspace{64px}=(9, 7)+(9, 1)+(73, 1)\)
\(\hspace{64px}=(81-7, 63+9)+(73, 1)\)
\(\hspace{64px}=(74, 72)+(73, 1)\)
\(\hspace{64px}=(5402-72, 5256+74)\)
\(\hspace{64px}=(5330, 5330)\)
\(\hspace{64px}=(1, 1)\)
（算出17）\((1, 1)=(3, 1)+(4, 1)+(5, 1)+(47, 1)\)
（右辺）\(=(12-1, 4+3)+(5, 1)+(47, 1)\)
\(\hspace{64px}=(11, 7)+(5, 1)+(47, 1)\)
\(\hspace{64px}=(55-7, 35+11)+(47, 1)\)
\(\hspace{64px}=(48, 46)+(47, 1)\)
\(\hspace{64px}=(2256-46, 2162+48)\)
\(\hspace{64px}=(2210, 2210)\)
\(\hspace{64px}=(1, 1)\)

（参考）
\((a+2, a)+(a+1, 1)\)
\(=((a+2)(a+1)-a, a(a+1)+a+2)\)
\(=(a^2+2a+2, a^2+2a+2)\)
\(=(1, 1)\)

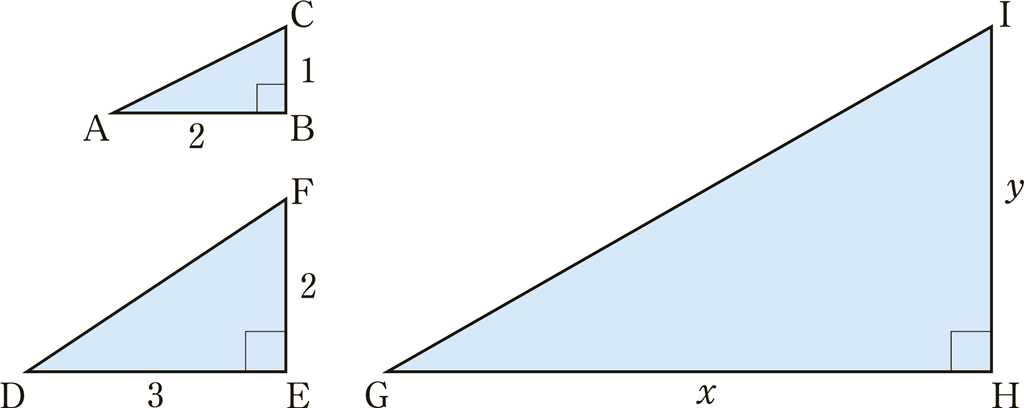
\((2, 1)+(3, 2)=(2\cdot 3-1\cdot 2, 1\cdot 3+2\cdot 2)=(4, 7)\)

\(\tan\angle \text{G}=\frac{7}{4}\)

最小の自然数 \(x, y\)は　\(x=4, y=7\)

　加法 \(\color{#ff0000}{(a, b)+(c, d)=(ac-bd, bc+ad)}\) については

\(\tan\theta_1=\frac{b}{a},\ \tan\theta_2=\frac{d}{c}\) とすれば　\(\theta_1\rightarrow\ \frac{b}{a},\ \theta_2\rightarrow\ \frac{d}{c}\)

加法定理より，\(\tan(\theta_1+\theta_2)=\frac{bc+ad}{ac-bd}\) であるから　\(\theta_1+\theta_2\rightarrow\ \frac{bc+ad}{ac-bd}\)

よって，加法 \(\color{#ff0000}{(a, b)+(c, d)=(ac-bd, bc+ad)}\) と定義する。

　減法 \(\color{#ff0000}{(a, b)-(c, d)=(ac+bd, bc-ad)}\) については

加法定理より，\(\tan(\theta_1-\theta_2)=\frac{bc-ad}{ac+bd}\) であるから　\(\theta_1-\theta_2\rightarrow\ \frac{bc-ad}{ac+bd}\)

よって，加法 \(\color{#ff0000}{(a, b)-(c, d)=(ac+bd, bc-ad)}\) と定義する。

　（参考）複素数平面に対応して考えることもできる。

\(\alpha=a+bi, \beta=c+di\) とすると

\(\alpha\beta=(a+bi)(c+di)=(ac-bd)+(bc+ad)i\)

\(\frac{\alpha}{\beta}=\frac{a+bi}{c+di}=\frac{(ac+bd)+(bc+ad)i}{c^2+d^2}\)

また

\(arg\alpha+arg\beta=arg\alpha\beta\)

\(\arg\alpha-arg\beta=arg\frac{\alpha}{\beta}\)

であり

\((a, b)=arg\alpha, (c, d)=arg\beta\)

として捉えると

加法 \((a, b)+(c, d)=(ac-bd, bc+ad)\)
減法 \((a, b)-(c, d)=(ac+bd, bc-ad)\)
が定義される。

また，加法については複素数の積に帰着できるので
交換法則 \((a, b)+(c, d)=(c, d)+(a, b)\)
結合法則 \(\{(a, b)+(c, d)\}+(e, f)=(a, b)+\{(c, d)+(e, f)\}\)
が成り立つ。

　これまで，\((a, b)\) については直角三角形の直角を挟む2辺が整数の場合を扱い，\(\frac{b}{a}\) が有理数になる場合を扱ってきたが，正接の加法定理は実数全体で成り立つので，\(a, b\) を実数全体に拡張しても差し支えない。

（例1）

\((\sqrt{3}, 1)+(\sqrt{3}, 1)=(3-1, \sqrt{3}+\sqrt{3})=(2, 2\sqrt{3})=(1, \sqrt{3})\)

\(\frac{\pi}{6}+\frac{\pi}{6}=\frac{\pi}{3}\) として確認する。

（例2）

\((1, 1)-(\sqrt{3}, 1)=(\sqrt{3}+1, \sqrt{3}-1)=(1, \frac{\sqrt{3}-1}{\sqrt{3}+1})=(1, 2-\sqrt{3})\)

\(\frac{\pi}{4}-\frac{\pi}{6}=\frac{\pi}{12}\) (\(\tan\frac{\pi}{12}=2-\sqrt{3}\) より)として確認する。

　\(y=\tan x\) は下図のグラフになるが，定義域を \(-\frac{\pi}{2}\lt x \lt \frac{\pi}{2}\) とすると逆関数 \(y=\tan^{-1}x\) が存在する。

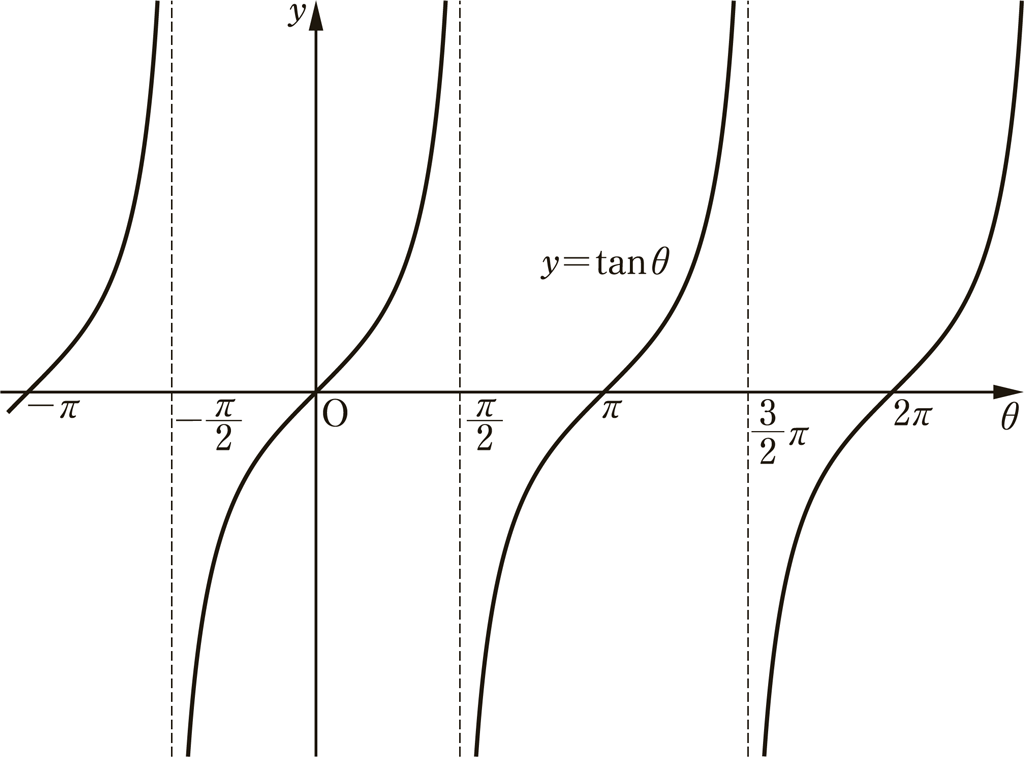
　逆関数 \(y=\tan^{-1}x\) のグラフは下図のようになり，正接の値と角は1：1対応である。

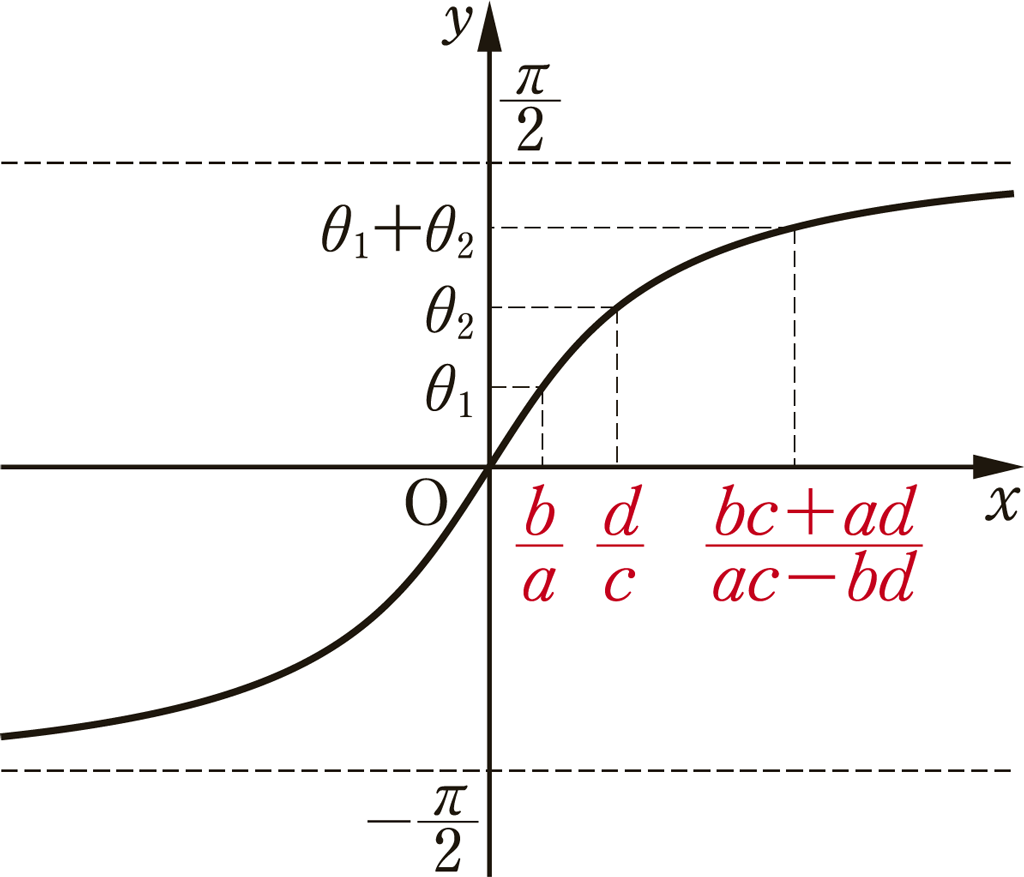
\(\theta_1=(a, b)=\tan^{-1}\frac{b}{a},\ \theta_2=(c, d)=\tan^{-1}\frac{d}{c}\)

とすると

\(\theta_1+\theta_2=(a, b)+(c, d)=(ac-bd, bc+ad)=\tan^{-1}\frac{bc+ad}{ac-bd}\)

として表現される。

　実際は，\(\theta_1+\theta_2\lt \frac{\pi}{2}\) も考えられるので，図はイメージである。

　演算を角として扱う場合は，最終的に角の大きさに注意する。
　定義された加法，減法はあくまでも正接としての対応であり，角の演算としては，演算の結果からどのような角が適しているかどうか吟味が必要になる。

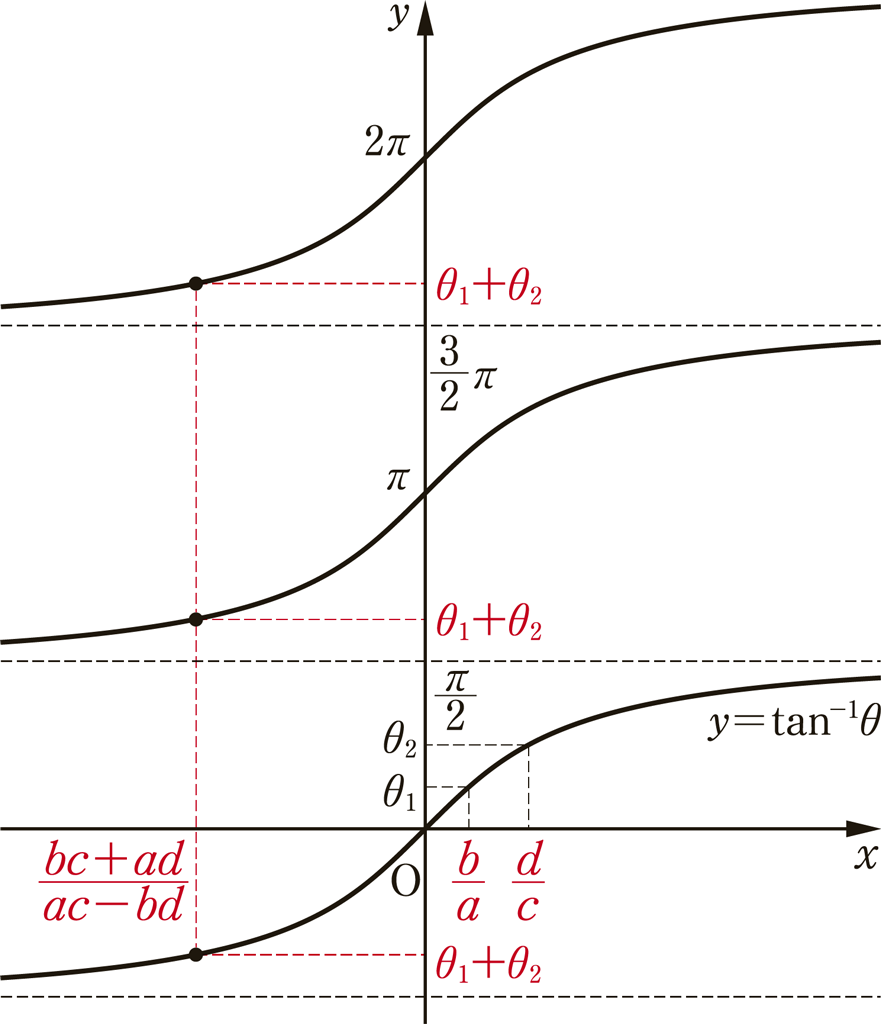
（例1）

\((-1,\ \sqrt{3})+(-1,\ \sqrt{3})=(1-3,\ -\sqrt{3}-\sqrt{3})\)

\(=(-2,\ -2\sqrt{3})=(1,\ \sqrt{3})\)

ここで，\((-2, -2\sqrt{3})=\frac{4}{3}\pi\)，\((1, \sqrt{3})=\frac{\pi}{3}\) である。

正接としてはお互いに \(\tan\theta = \sqrt{3}\) であるが，2つの角の和は \(\frac{4}{3}\pi\) で調整する。

（例2）

\((1, \sqrt{3})+(\sqrt{3}, 1)=(\sqrt{3}-\sqrt{3}, 3+1)=(0, 4)\)

正接が存在しないので，2つの角の和は \(\pm\frac{\pi}{2}\) の位置として扱い，和は \(\frac{\pi}{2}\) で調整する。

（例3）

\((-1, 1)+(-1, 1)=(1-1, -1-1)=(0, -2)\)

正接が存在しないので，2つの角の和は \(\pm\frac{\pi}{2}\) の位置として扱い，和は \(\frac{3}{2}\pi\)で調整する。

（参考）複素数の積で考えることもできる。

（例1）\((-1+\sqrt{3}i)^2=-2-2\sqrt{3}i\)

　\(arg(-2-2\sqrt{3}i)=\frac{4}{3}\pi+2n\pi\)

（例2）\((1+\sqrt{3}i)(\sqrt{3}+i)=4i\)

　\(arg(4i)=\frac{\pi}{2}+2n\pi\)

（例3）\((-1+i)^2=-2i\)

　\(arg(-2i)=\frac{3}{2}\pi+2n\pi\)

　いずれも，\(n\) を整数として調整すればよい。

正接の数学散歩

正接に関して，大学入試でよく扱われる問題をまとめた資料集です。（資料➃－2）

1. \(\tan2\theta\) から \(\tan\theta\) を求める。

2. 級数 \(\displaystyle\sum_{n=1}^{\infty}\tan^{-1}\frac{1}{n}\) の極限

3. 2直線のなす角

4. 見込む角の最大

5. 最大・最小

6. 積分

おわりに

　「Tanθを楽しもう」と題して思うままに述べてみた。実際は楽しむどころか，どんどん深みにはまって苦しんだのが本音である。
　特に1つの角を複素数の積の偏角として考える着想はよかったものの，4つの角の和となると計算が極めて複雑で苦労した。
　そのような中，角を分解して表現する連鎖探索法は極めて有効な方法であることが分かった。
　しかしながら，効果的な連鎖探索法であっても，全く異なるタイプでも結果的に重複する場合が生じることがあることや，連鎖探索によって必ずしもすべてが網羅されるわけでもないことは留意しておかなければならない。
　どのようにすればこのようなことを事前に把握できるのか，これからの課題でもある。こうした操作をプログラミングできればさらに面白いはずである。
　今回，加法や減法の演算として整理したが，ある程度深掘りできたのではないか。高校生にも十分理解ができる内容になったのではないかと思う。
　何より私自身の勉強にもなったのは事実であり，正接を楽しく学んだ。
　拙い研究になったが，お気づきの点があれば ご指導ご鞭撻いただきたい。
　どうぞ，忌憚のないご意見をお聞かせください。

長崎大学
中川 幸久

【講師】