
カーペットなどの床の上に置いてあるテーブルがガタガタしています。テーブルの脚の長さを調節してガタガタを解消できることもあります。調節できないテーブルの場合,床がゆがんでいたらガタガタは直らないかもしれません。そんなとき,紙でも挟むしかないかな…とあきらめていませんか?
実は,テーブルをくるくる回せる状況だったら,数学の定理を使ってガタガタを解消することができます。
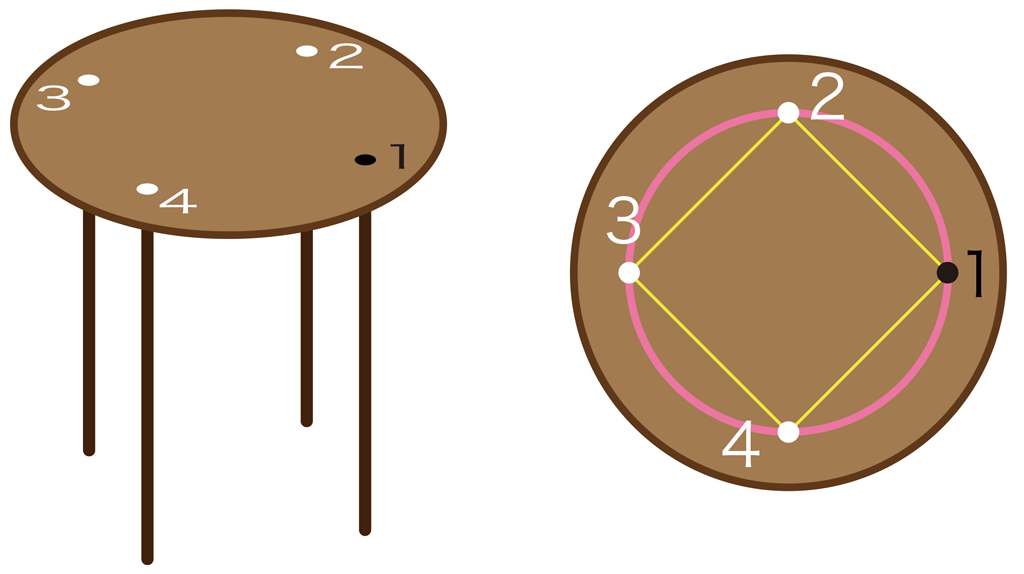
次の写真は,カーペットの上に置かれたテーブルです。テーブルの脚は4本あって,正方形に配置されています。各脚の長さは等しいとします。
【疑問】テーブルがガタガタします。ガタガタしない位置はあるでしょうか。

【答え】あります。中間値の定理を使って証明できます。
【証明の骨子】
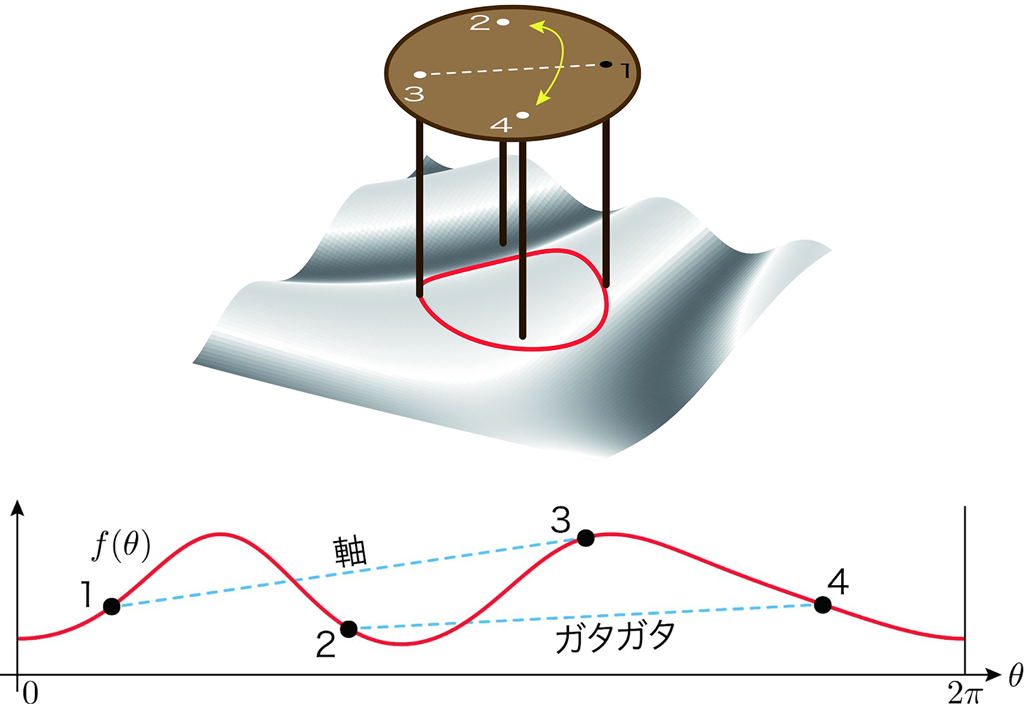
脚の番号を反時計回りに1,2,3,4とします。脚は上から見ると正方形に配置されていて,脚の足先は同一円周上(ピンク色)に配置されていると仮定できます。
以下の図のように,ゆがんだ床を曲面で表すと,曲面上の赤色の線はピンク色の円をゆがんだ床に射影したときの閉曲線です。
正方形の配置を維持したまま,4点をピンク色の円周上でくるくる回して,ガタガタしない箇所を見つけることが目標です。
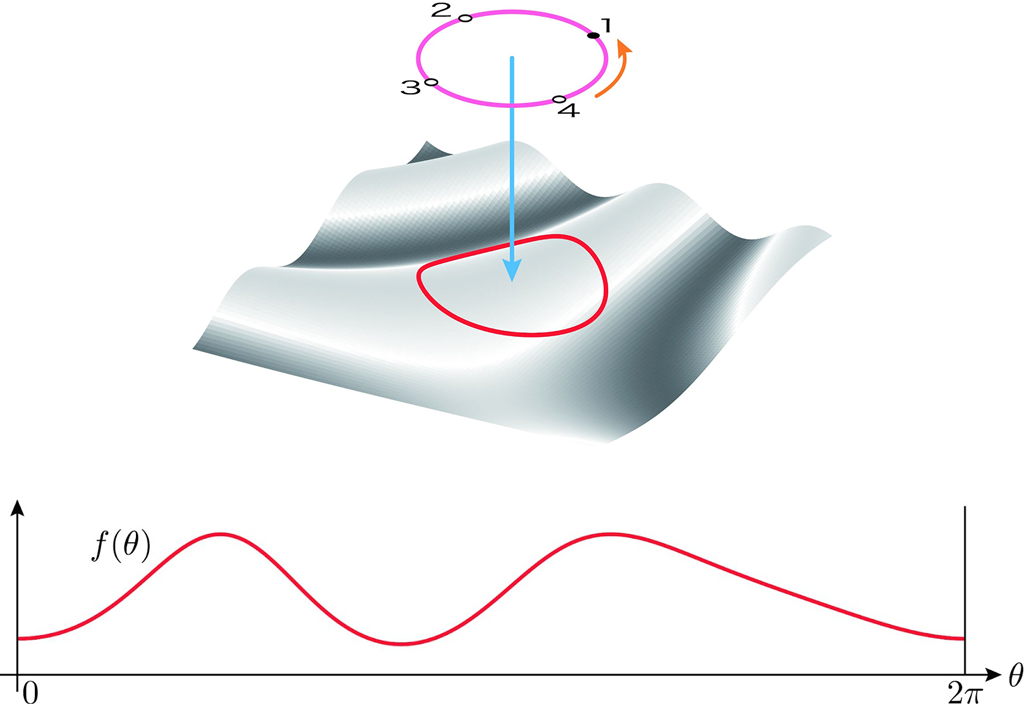
回転角を \(\theta\),床の高さを \(f(\theta)\) とします。赤色の線は横軸を \(\theta\) として,連続な周期関数のグラフとして表現されます。
脚1を無視して脚2,3,4を床につけたとき,床の3点を通る平面をPとします。もし,脚1の足先が平面P上にあったら,床がゆがんでいても脚1,2,3,4の足先は同一平面上にあるのでテーブルはガタガタしません。
脚1の足先(以下,足先1と書きます)が平面P上にないとき,次の2つの場合が考えられます。
(場合1)
実際にテーブルを置いたとき,足先2,4が床の上で,1,3方向にテーブルがガタガタしたとします。
この状況をグラフでみると,足先2,4が床の高い点で,足先1,3がそれより低い点となっていることがよくわかります。
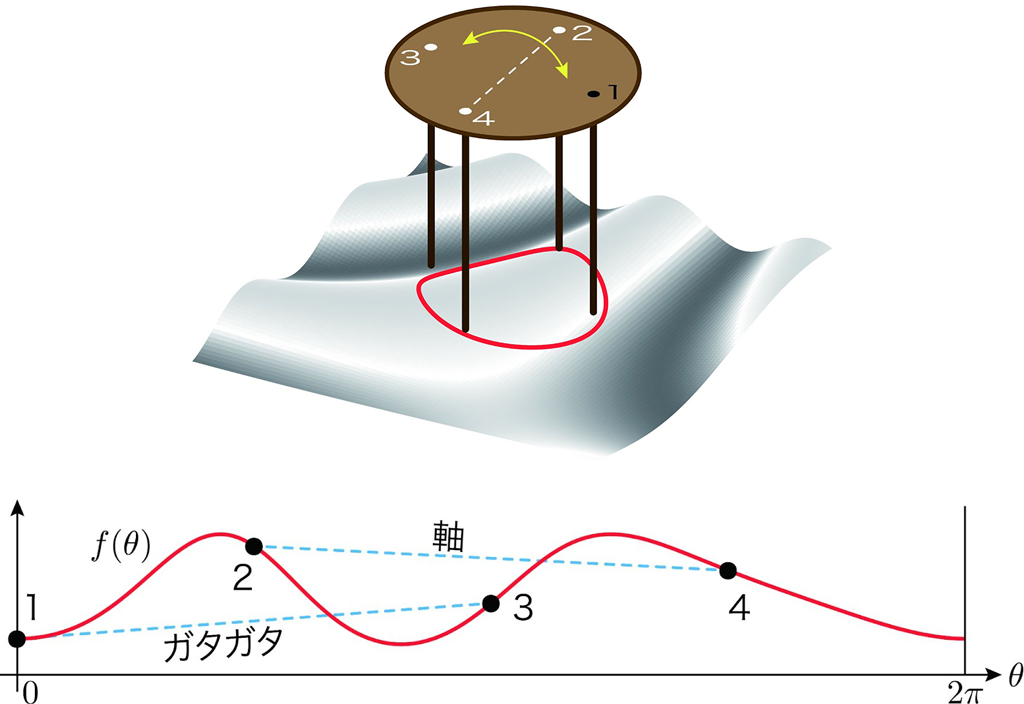
このとき,足先1は平面Pの下側にあります。
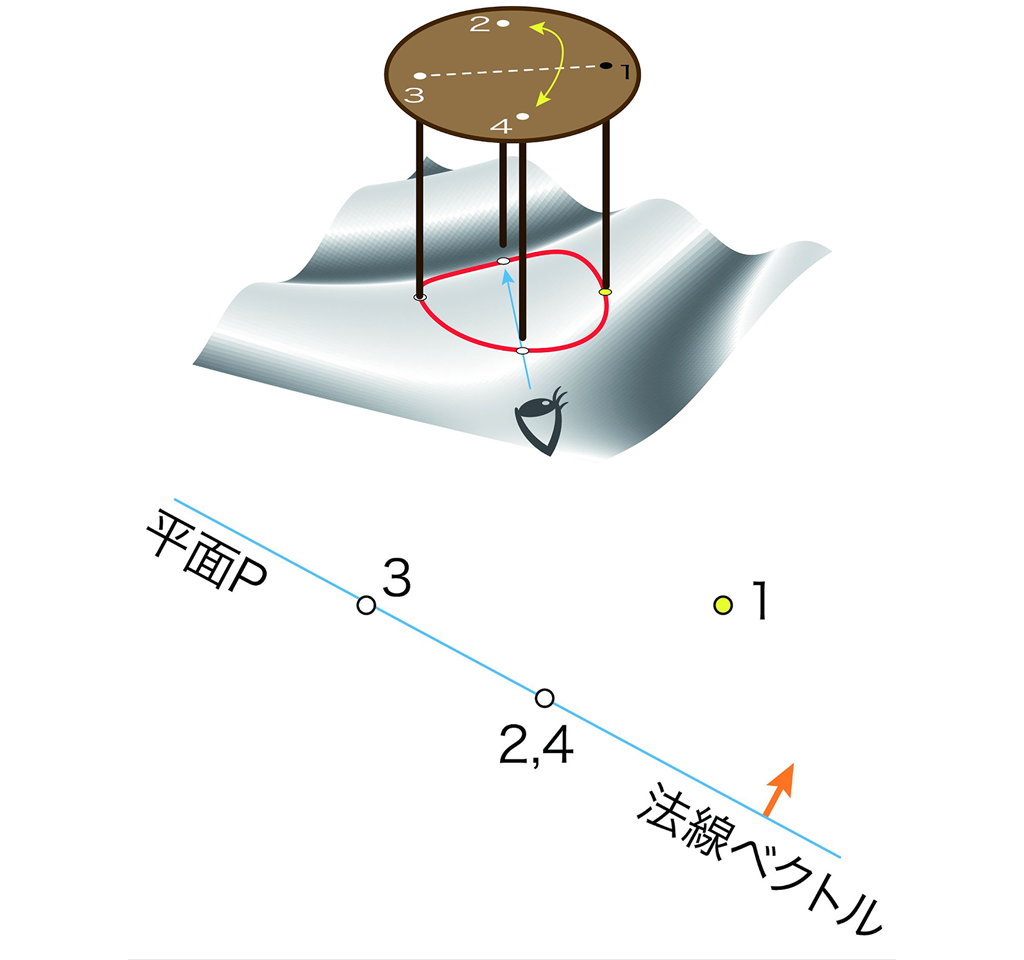
足先2,4が一致するほぼ真横から見ると,以下のようなイメージ図になります。平面Pの下側という意味は,図の法線ベクトルの逆向き側にあるということです。
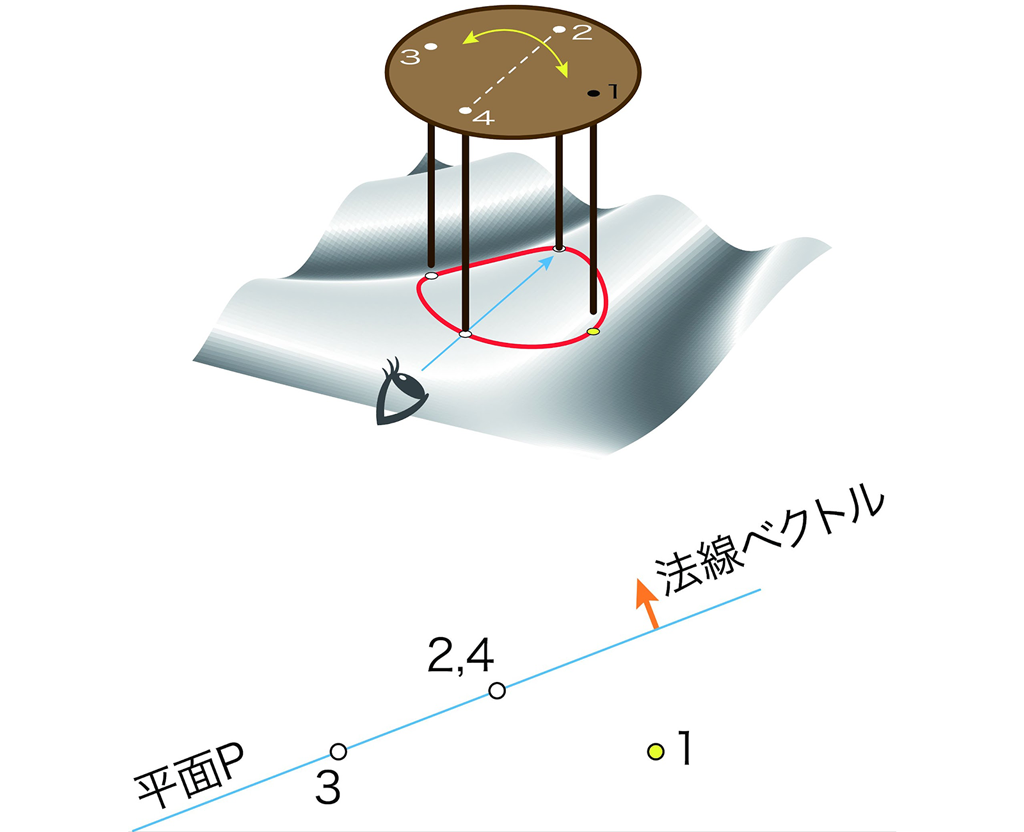
(場合2)
さらに,テーブルを回転させて,足先1,3が床の上で,2,4方向にテーブルがガタガタするようになったとします。
この状況をグラフでみると,足先1,3が床の高い点で,足先2,4がそれより低い点となっていることがよくわかります。
このとき,足先1は平面Pの上側にあります。
足先2,4が一致するほぼ真横から見ると,以下のようなイメージ図になります。平面Pの上側という意味は,図の法線ベクトルの向かう側にあるということです。
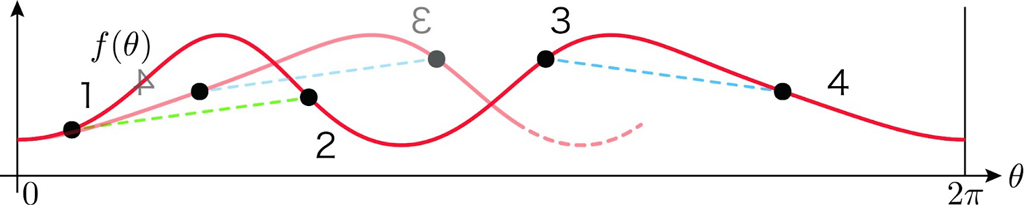
場合1,2と中間値の定理より,足先1が平面P上にあるようなテーブルの回転角が存在します。このときの条件もわかっていて,下図のように,足先1→2の傾きと足先4→3の傾きが等しいとき,4点が同一平面P上に存在します。(証明終)
【疑問の深掘り】
ガタガタを解消するには上の“証明”で十分なのですが,数式がないと「数学的な証明」になっていないと思われるかもしれません。
数式を使うから数学的な証明になるわけではないですが,確かに,数式を使わない説明は,思わぬ落とし穴がある場合もあります。また,4本の脚の足先が同じ平面P上に乗っているからといって,その平面Pが水平であるかどうかは別問題です。
詳しくはこちらの説明をご覧ください。
ボルツァーノの贈り物
北半球の日本から南半球のオーストラリアに飛行機で飛ぶと,途中で必ず赤道を横切る。当たり前であるが,これは中間値の定理の結果である。中間値の定理はさまざまな形で表現されるが,次の表現がもっとも単純であろう。
関数 \(f\) は閉区間 \([ a,\ b ]\) で連続とする。
このとき,\(f(a)f(b)\lt 0\) ならば,\(f(c)=0\) を満たす \(c\ (a \lt c \lt b)\) が存在する。
中間値の定理はボルツァーノ(Bernard P.J.N. Bolzano,1781-1848)により1817年の論文で示された。中間値の定理は図を見ればほとんど明らかに見える命題だけに,何を証明すれば証明したことになるのかがピンとこない。
原論文のタイトルは,『反対の符号の結果を与える任意の2つの変数の間には方程式の実根が少なくとも1つ存在するという定理の純粋に解析的な証明』という長いものであった。図を見れば明らかなものを「図と運動の直観」に頼らずに,関数の連続性についての厳密な定義に基づいて「純粋に解析的な」手法を用いて証明されたところに意義がある。
このタイトルに,ボルツァーノの強い主張と矜持が現れているようにみえる。タイトルからわかるように,中間値の定理はしばしばボルツァーノの定理とも呼ばれる。
チェコ共和国・プラハ市の旧市街の中心に旧市街広場がある。広場西側の旧市庁舎の塔に天文時計が掛かっていて,毎時定刻になると時計仕掛けが作動する。東側には2本の塔が目立つティーン教会が立っている。
教会を左に見ながらツェレトゥナー通りを東に向かってしばらく進むと,右側の角に黒い聖母の家と呼ばれるキュビズム建築の博物館が見えてくる。その向かいの建物にベルナルド・ボルツァーノのレリーフが飾ってある。その建物の1階はボルツァーノ小道となっていて,かつて行ったときには,その地下にカフェ・ボルツァーノがあった。

「ここに居住し死去/ベルナルド・ボルツァーノ/優れた数学者・哲学者/1781.10.5-1848.12.18」(筆者撮影)
※「つい考えてしまう数学」の記事一覧はこちら
1970年東京生まれ。早稲田大学理工学部数学科卒業。東京大学大学院数理科学研究科数理科学専攻博士課程修了。現在,明治大学理工学部数学科専任教授。博士(数理科学)。専門は応用数理,特に界面現象の数理解析。実験を採り入れた数学の講義で定評がある。
| 著書: | 『実験数学読本』①・②・③ (日本評論社),『次元解析入門』,『界面現象と曲線の微積分』,『動く曲線の数値計算』(以上共立出版),『大学数学の教則』(ちくま学芸文庫),『公式は覚えないといけないの?』(ちくまプリマー新書),他。 |
その他のコンテンツ
