
近年の大学入試問題を通して,自分がどのように指導しているかを紹介していく内容にしようと考えています。みなさんの日々の指導に少しでも役立つような中身にできればと思っていますので,どうぞお付き合いください。
不等式とグラフ
大学入試において,圧倒的に出題率が高いのは「関数分野」です。
私が生徒たちによく言うことの1つに「関数はグラフを活用しろ!」があります。ほとんどの関数問題はグラフを使って解決する(三角関数は単位円の方が優先度が高いけど)のですが,多くの生徒が適切な図・グラフを描けないし,描こうとしないものです。
例えば,高校2 年生に久しぶりに「2次不等式」を解かせると,まぁ酷い有様だったりするものです。(ご経験があるのではないでしょうか?)
さて,今回紹介する1 問目はこちらです。
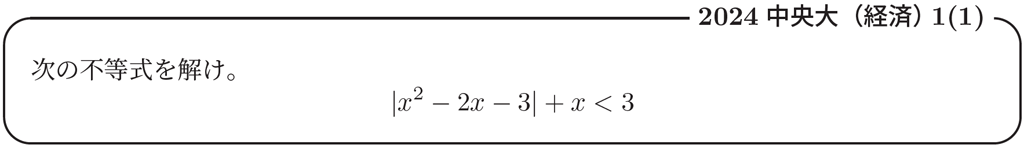
主な解法としては
| (イ) | \(x^2-2x-3 \geqq 0\) の場合と \(x^2-2x-3 \leqq 0\) の場合に分けて,ゴリゴリ計算 |
| (ロ) | \(y=|x^2-2x-3|\) と \(y=-x+3\) のグラフの比較 |
| (ハ) | \(y=|x^2-2x-3|+x\) と \(y=3\) のグラフの比較 |
といったところでしょう。
生徒たちに解かせると,(イ)に走って,場合分けと解の不等式で混乱してしまいがちです。
(ロ)も悪くはないのですが,曲線と斜めの直線がどのように交わるかを調べるのが,かえってメンドウな場合もあるので注意が必要です。
私は(ハ)がオススメです。この手のグラフに慣れている人なら,\(y=|x^2-2x-3|\) のグラフの「地面」を \(y=x\) に変換するとでもイメージして,次図のような感じだと瞬時に判断できます。(解答例はこちら)
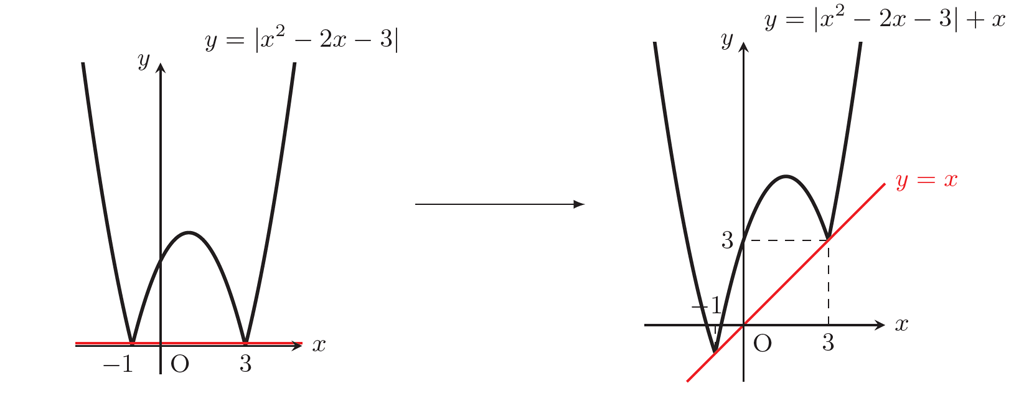
導関数の符号
ある書籍に次のような例題と解答が載っていました。
解答
\(y’=3x^2-6x=3x(x-2)\)
\(y’=0\) とすると \(x=0,2\)
\(y\) の増減は次の表のようになる。
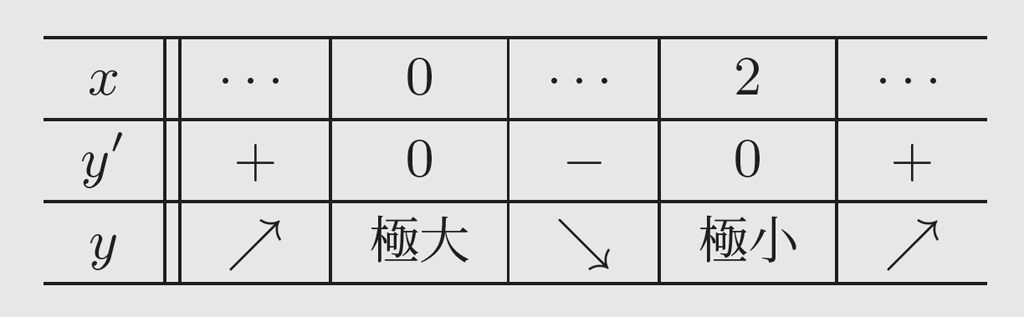
\(x=0\) で極大値 \(\mathbf{3}\),\(x=2\) で極小値 \(\mathbf{-1}\)
をとる。
これだけでは,増減表の2 段目の「符号」が把握できず,3 段目の矢印(増減)が書けないはずです。したがって,指導する上では「 \(y’\) の符号の説明」を補うことが大切です。
いくつかの方法が考えられますが,自分はグラフを描くように指導しています。上記の例では次図(左)のような図を描いて説明するし,生徒たちにも描くことを要求します。
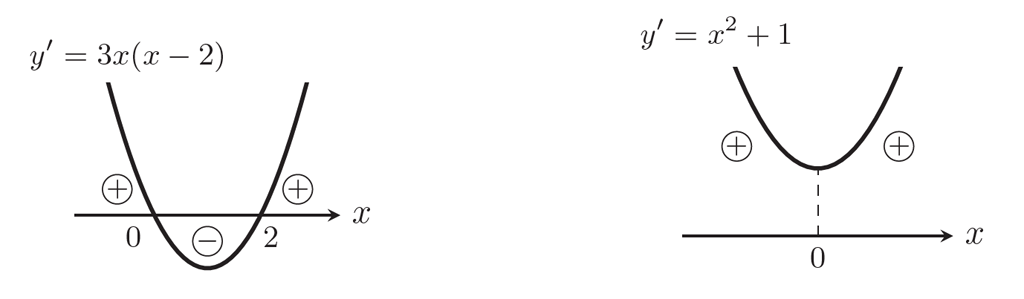
例えば \(y’=x^2+1\) となると「 \(x^2+1=0\) より \(x=\pm i\) 」とか言い出す答案を何度見てきたことか…。これも上図(右)のようにグラフを描くようにしていれば,符号に悩みません。
関数 \(f(x)\) の増減を調べるときには導関数 \(f'(x)\) の符号を調べることが大切です。そのために \(\color{red}{y=f'(x)}\) のグラフを描く習慣をつけるべきです。(数学Ⅲでは,符号を調べたい部分だけを取り出してグラフを描くこともあります。)
とくに難関大志望の生徒には,この習慣を身につけさせたいものです。そして,その習慣がついた後に考えさせたい問題がこちらです。
1つ目の条件はゴリゴリ計算することで処理できます。すると
\(a=-3m-\dfrac{3}{2}\)
\(b=3m^2+3m+\dfrac{1}{2}\)
\(c=-m^3-\dfrac{3}{2}m^2-\dfrac{1}{2}m\)
が得られて
\(f'(x)=3x^2+(-6m-3)x+\left(3m^2+3m+\dfrac{1}{2}\right)\)
となります。ここで,\(y=f'(x)\) のグラフの様子を調べる力が試されます。(解答例はこちら)
第1回は以上になります。どうでしょうか。楽しんでいただけましたか?
次回は予備校業界の闇に迫ります!共通テスト対策としても役立つ,関数グラフの面積計算の技巧を紹介します。引き続きよろしくお願いします♪
※「大山壇の入試問題Pick Up!」の記事一覧はこちら
宇都宮北高校,東北大学理学部数学科卒。
2006年度から代々木ゼミナールの講師となり,現在は新宿本部校と札幌校に出講しています。対面・映像の授業の他にも,テキスト・模試・解答速報の作成なども行っています。
もっと毒をはいている大山を見たい方は,X(旧Twitter)をどうぞ!→ @dan_oyama_0206
《著書》
・『全国大学入試問題正解』(旺文社)解答執筆(京大,一橋大,東北大など)
・『整数分野別標準問題精講』(旺文社)
・『全レベル問題集 3 』(旺文社)
・『全レベル問題集 5 』(旺文社)
・『大山壇の基本から身につける計算力IA』(KADOKAWA)
・『大山壇の基本から身につける計算力IIB』(KADOKAWA)
その他のコンテンツ
- 主体的・対話的で深い学び
- 数学的な見方・考え方
- 知識・技能
- 思考力・判断力・表現力
- 主体的に学習に取り組む態度
- ICT
- デジタル教科書
- Dマークコンテンツ
- 評価
- 指導書

