
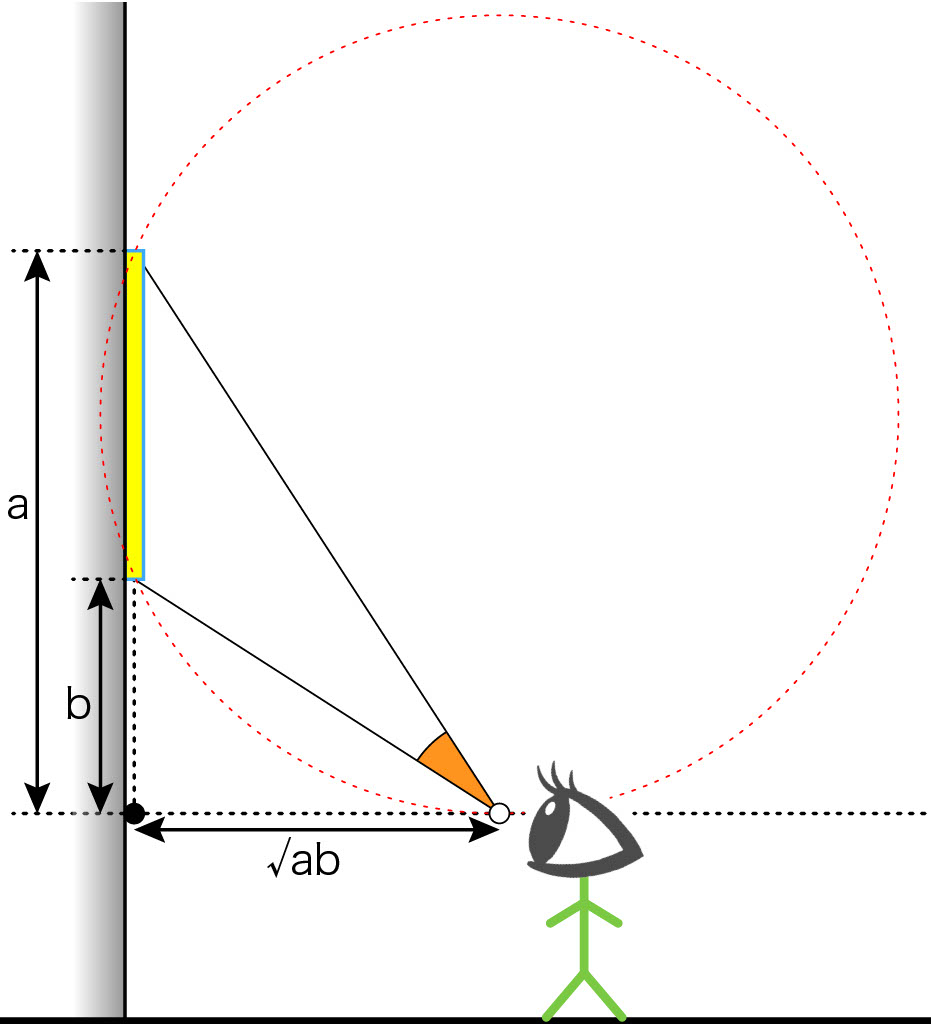
その距離を達成する点は,絵画の上端と下端を通り,目線の高さの線に接する円の接点でした。
今回は,この知見を,ラグビーにおけるコンバージョンキックの位置取りに応用しましょう。
コンバージョンキックとは,トライの後にゴールポストの間のクロスバーの上を狙ってキックする得点方法です。

インゴール内にトライした位置(黄色丸)を通り,タッチラインに平行な直線上(黄色線)の好きな位置からキックすることができます。
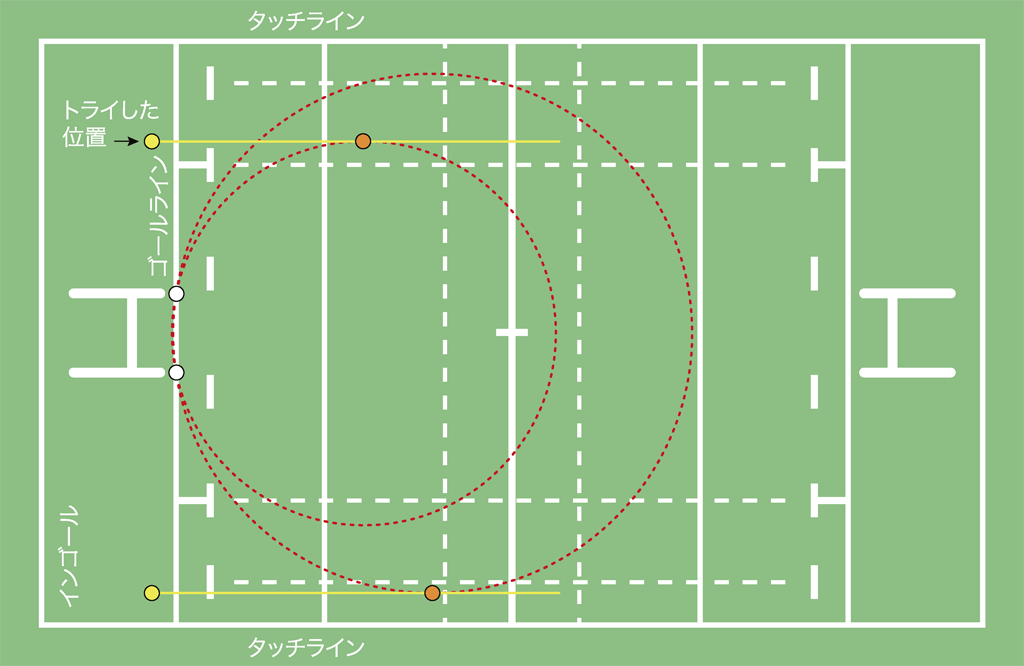
【疑問】どこからキックすればよいでしょうか。
【考察】グラウンドを真上から見て,2本のゴールポストを絵画の端点に見立てれば,前回の絵画を見るときの最大視角を得る位置の話を応用することができそうです。
つまり,ゴールポストの2点を通り黄色線に接する円を考えて,その接点から見ると最大視角を得るので,キックで狙うべき2本のゴールポストの間が広く見えて,キックしやすくなるわけです。
※実際は,キッカーの技量や角度の得手不得手に依存するでしょうから,以上の話は,最大視角になるのはどこかという観点だけからの考察です。
トライする位置(黄色丸)はさまざまです。それらの位置に応じて最大視角を得る点(オレンジ色丸)が決まります。

オレンジ色丸が増えていくと,何らかの曲線の上に乗っているのかどうか気になってきます。
【深堀りする疑問】オレンジ色丸が乗っていると思われる曲線を求められるでしょうか。
【考察】ゴールラインを \(x\) 軸,ゴールポストの中心を原点 \(\text{O}\) とし,原点を通りタッチラインに平行な直線を \(y\) 軸とします。(各軸の向きは図のようにとります。)
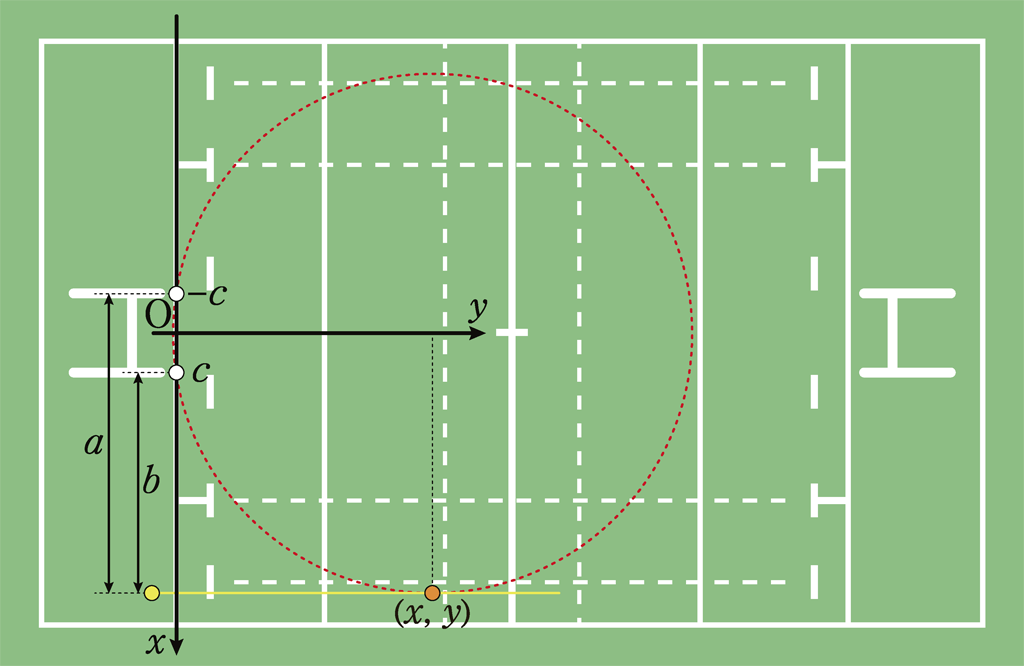
ゴールポストの位置を \(x=\pm c\) とおきます。
トライした位置を \(x>0\) として,遠い方のゴールポストまでの距離を \(a\),近い方のゴールポストまでの距離を \(b\) とすると,
\(a=x+c\) , \(b=x-c\)
となります。
最大視角を得る点のゴールラインからの距離を \(y\) とすると,\(y=\sqrt{ ab }\) だから,方程式
\(y^{ 2 }=(x+c)(x-c)=x^{ 2 }-c^{ 2 }\)
を得ます。
これは,直線 \(y=\pm x\) を漸近線にもつ双曲線で,\(2c\) はゴールポスト間の距離です。規定では \(5.6\) メートルだから \(c=2.8\) メートルです。

図をみるとわかるように,双曲線は原点から離れるとすぐに漸近線に接近します。
漸近線の傾きは \(\pm 45^{ \circ }\) だから,大雑把にいって,キックする位置とゴールポストの真ん中を結ぶ直線が,タッチライン( \(y\) 軸)あるいはゴールライン( \(x\) 軸)と \(45^{ \circ }\) の角度をなすような位置のちょっとゴールライン側からゴールポストを見れば,概ね最大視角を得ることができます。
レギオモンタヌスの贈り物
レギオモンタヌス(Regiomontanus)は15世紀のドイツの天文学者・数学者です。少し珍しい名前に聞こえますね。彼はケーニヒスベルクのヨハン・ミュラー(Johann Müller)に生まれました。ケーニヒスベルク(Künigsperg)は王の山という意味で,そのラテン語表記はRegio Monteで,後にRegiomontanus となったといわれています。しかしそればかりではなく,彼はJohannes Molitoris de Künigspergとして大学に入学しました。その他にも,Johannes Germanus(ドイツ人ヨハン),Johannes Francus(フランケン出身のヨハン),Johann von Künigsperg(ケーニヒスベルク出身のヨハン),そしてガッセンディが伝記を書いた際に呼んだJoannes de Monte Regio(モンテ・レジオ出身のヨハン)というフランス語風の呼び名もあったようです。
呼び名の変遷はともあれ,幼少より数学と天文学に才能を発揮して,11才で大学に入学しました。彼の生きた時期は,コペルニクスの40年ほど前で,漫画『チ。』の舞台となった時期にほぼ重なります。(『チ。』に取り込まれているかどうかはわかりません。)40才の若さで急逝しました(ある著作を無価値であると批判して,その著者の2人の息子に殺害されたという説もあるが,ペスト菌による感染症の犠牲になった方が理由としてはもっともらしいでしょう)。絵画の最大視角の問題は,レギオモンタヌスの問題と言われています。彼はなぜこのような問題を考えたのか,動機も解き方も不明のようです。星の観測をしていたのだから,きっと視点とか視角をいつも気にしていたはずです。案外,日常の研究から思いついたのかもしれませんね。
1970年東京生まれ。早稲田大学理工学部数学科卒業。東京大学大学院数理科学研究科数理科学専攻博士課程修了。現在,明治大学理工学部数学科専任教授。博士(数理科学)。専門は応用数理,特に界面現象の数理解析。実験を採り入れた数学の講義で定評がある。
| 著書: | 『実験数学読本』①・②・③ (日本評論社),『次元解析入門』,『界面現象と曲線の微積分』,『動く曲線の数値計算』(以上共立出版),『大学数学の教則』(ちくま学芸文庫),『公式は覚えないといけないの?』(ちくまプリマー新書),他。 |
その他のコンテンツ
