

高い所にある銅像を見上げるとき,どこから見ると,全体が一番よく見えるか,場所選びにウロウロしませんか。
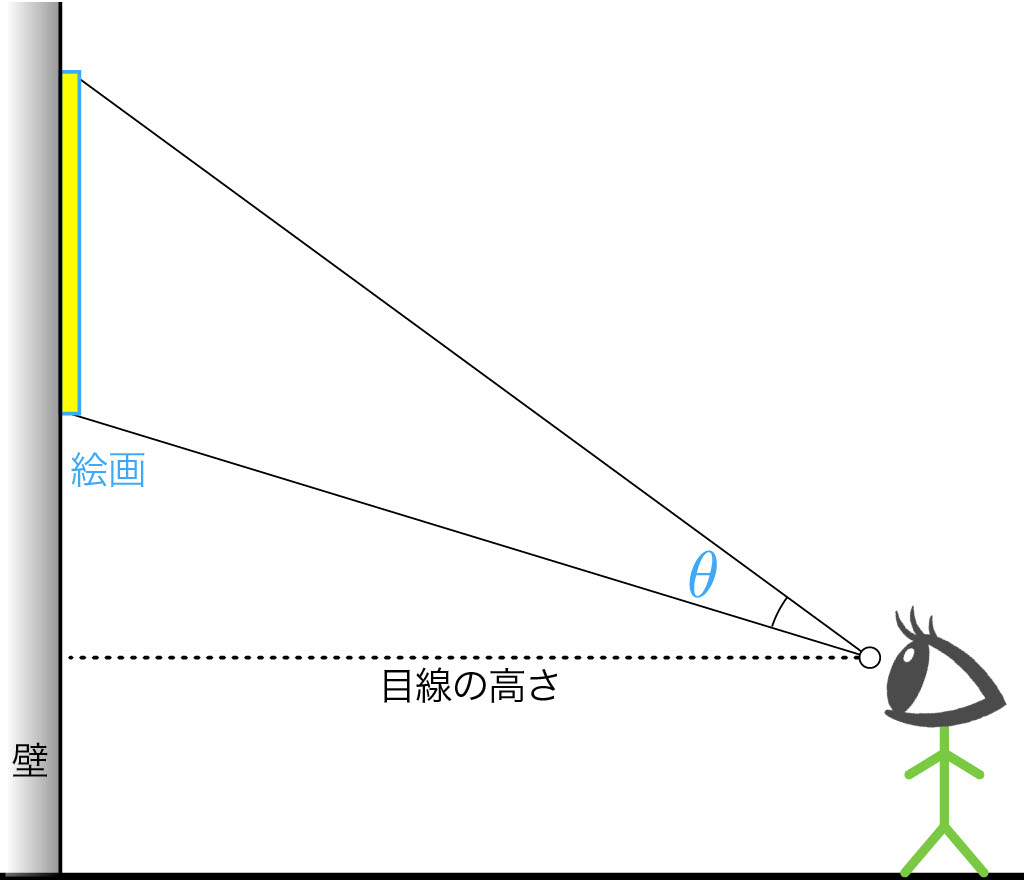
目線よりも高いところにある壁に掛かっている絵画を見るとき,一番よく見える場所にいきたいですよね。
図の角度\(\theta\)を,見込む角,視角などといいます。一番よく見える場所とは,視角が最大になる場所のことです。
【疑問】視角が最大になる場所はどこでしょうか。
【考察】目線の高さは変わらないとして,点線を目線の高さとすると,まずは,点線上に視角が最大になる点があるのかどうかを考えます。
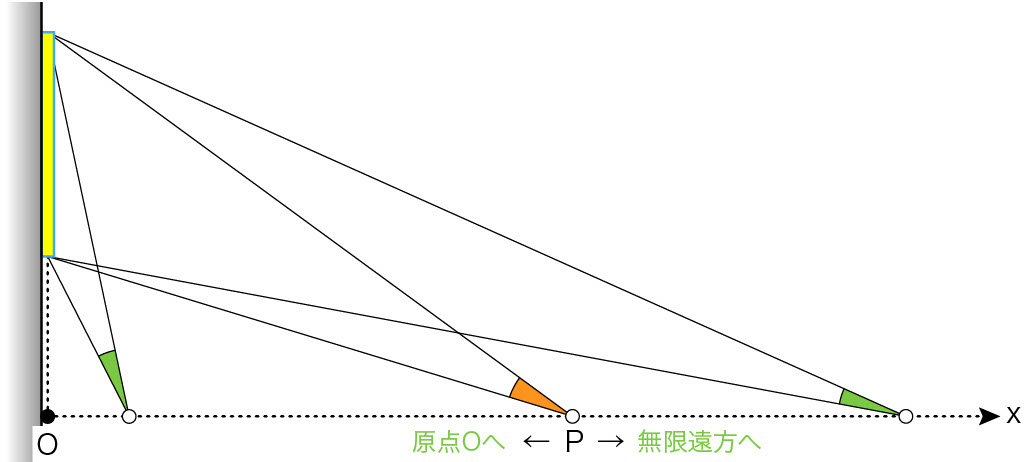
《\(\mathbf{O \leftarrow P}\)》
絵画の下の点を原点 とすると,\(\text{P}\)が\(\text{O}\)に一致したら視角0ですので,\(\text{P}\)が\(\text{O}\)に近づくと視角は0に近づきます。
《\(\mathbf{P \rightarrow }\) ∞》
\(\text{P}\)を原点から離れる方向に,限りなく動かしていくと,無限遠方で視角は0に近づきます。
視角は\(\text{P}\)を動かすと連続的に変化して,\(\text{P}\)が原点に近づいても,無限遠方に行っても0に近づきますので,\(\text{P}\)が原点でも無限遠方でもないどこかの点で視角の最大値をとることがわかります。
《なぜこんなことを言及するの?》
最大になる点はどこ?みたいな疑問に対しては,まず,最大になる点はあり得るのかを考えます。
なぜかというと,そんな点がないとわかったら,探すのは無駄ですから。そして,そんな点があるとわかったら,見つけてやろうと,俄然やる気がでますから。
一般に「(何らかの)最大になる点を求めよ」という問題がテストで出題される場合は,あるに決まっている前提で出題されることがほとんどです。もしそういう点の存在も含めて考えてほしい場合は,「最大になる点があればそれを求めよ」という問いかけになることが多いでしょう。
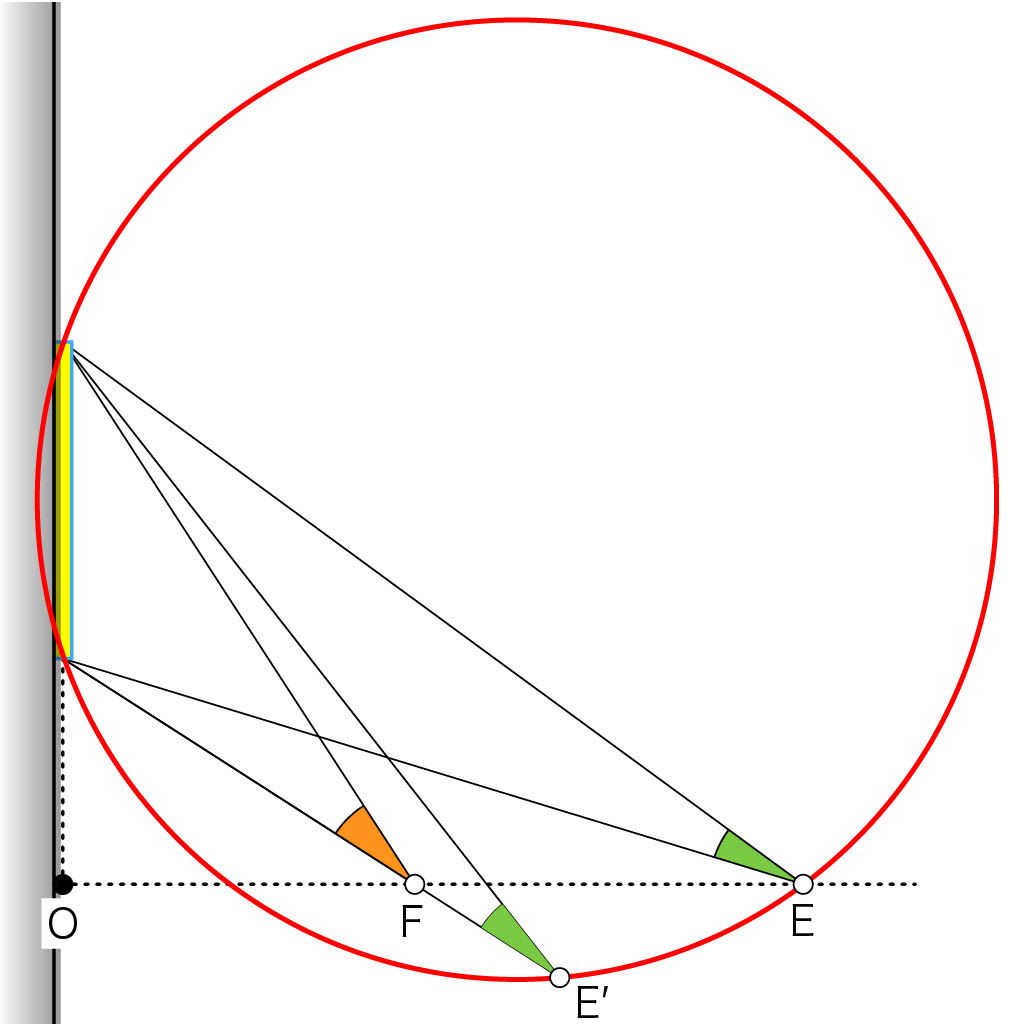
目線の高さの点線上に点\(\text{E}\)をとって,絵画の上端と下端と\(\text{E}\)を通る円を描きます。3点を通る円は必ず一つに決まります。
その円が\(\text{E}\)で点線と交差した場合,円の一部は点線より下側に飛び出します。
その飛び出した円弧のどこかに点\(\text{E}’\)をとります。\(\text{E}’\)から絵画の上端と下端にそれぞれ半直線を書くと,角\(\text{E}’\)ができます。
円周角の定理から
\(\angle \text{E}=\angle \text{E}’\)
です。
\(\text{E}’\)と絵画の下端(あるいは上端)を結ぶ直線と点線の交点を\(\text{F}\)とします。\(\text{E}’\)と同様に角\(\text{F}\)を作ることができます。このとき,必ず
\(\angle \text{F}\gt\angle \text{E}’\)
が成り立ちます。だから,点線上の点と絵画の上端と下端を通る円が点線と交差するとき,その点が作る角度よりも大きい角度になる点が点線上にあることがわかります。
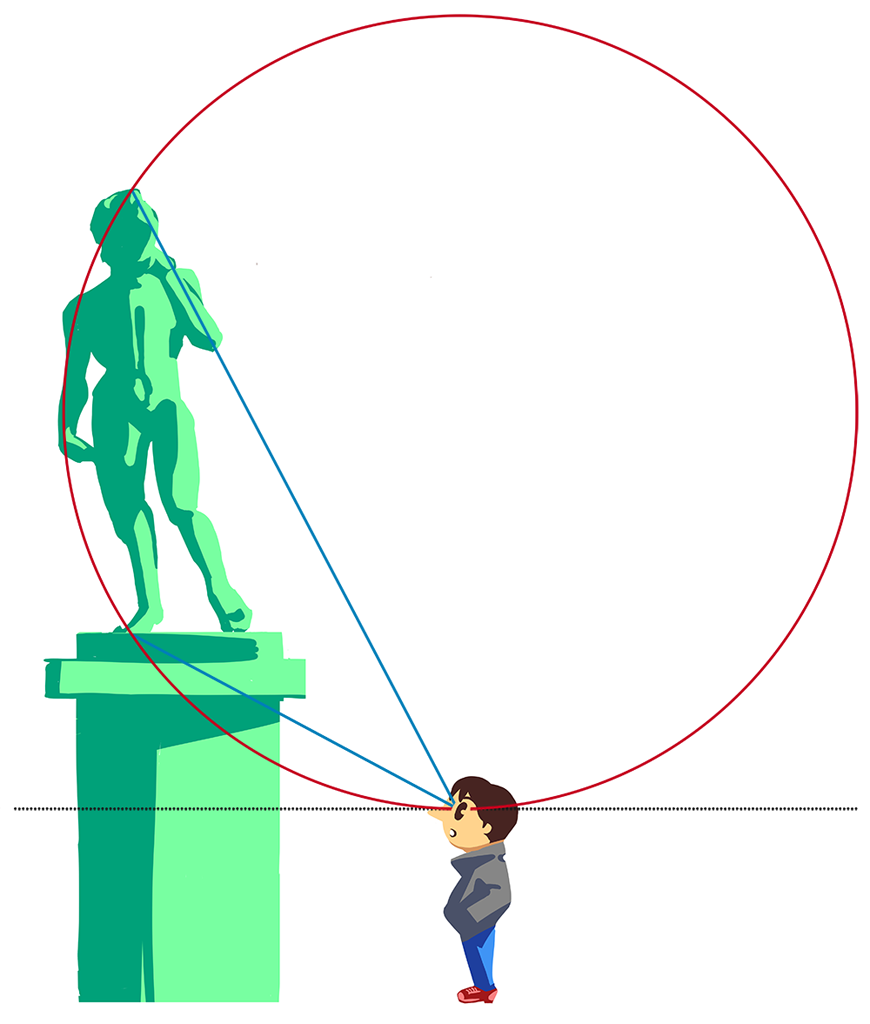
そこで,点線と交差しないような円を考えます。それは,点線に接する円です。そのような円はただ一つに決まります。
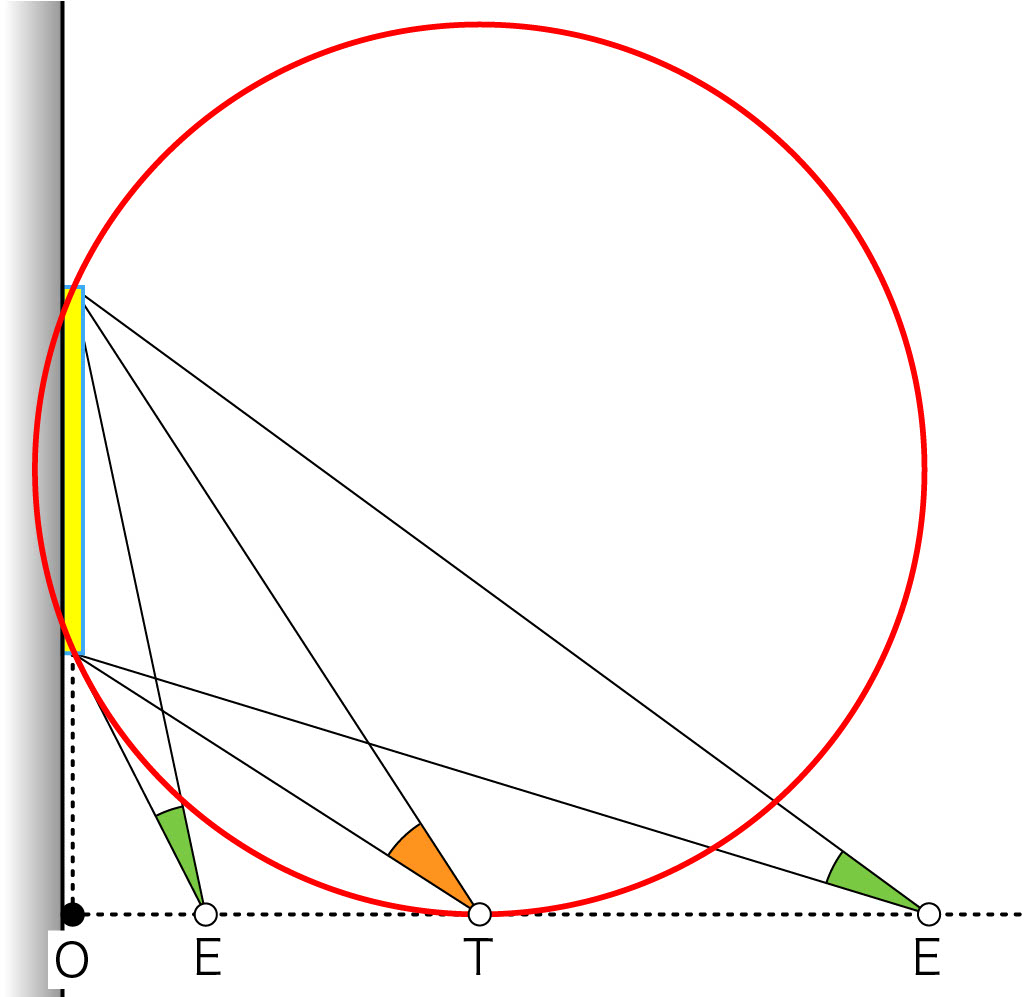
接点を\(\text{T}\)とします。(接線はtangentなので。)
接線上(点線上)で\(\text{T}\)以外の点\(\text{E}\)をとったとき,\(\text{T}\)における視角はいかなる点\(\text{E}\)における視角よりも大きくなります。
つまり接点\(\text{T}\)に立てば,視角は最大になります。
【新たな疑問】接点\(\color{red}{\mathbf{T}}\)はどこにあるのでしょうか? つまり,壁からどのくらい離れればよいのでしょうか。言い方を変えると,\(\color{red}{\mathbf{OT}}\)の長さは求まるでしょうか。
【考察】絵画の上端と下端をそれぞれ\(\text{A}\),\(\text{B}\)とし,
\(\text{OA}=a\text{,}\text{OB}=b\text{,}\text{OT}=x\)
とおき,\(x\)を求めます。
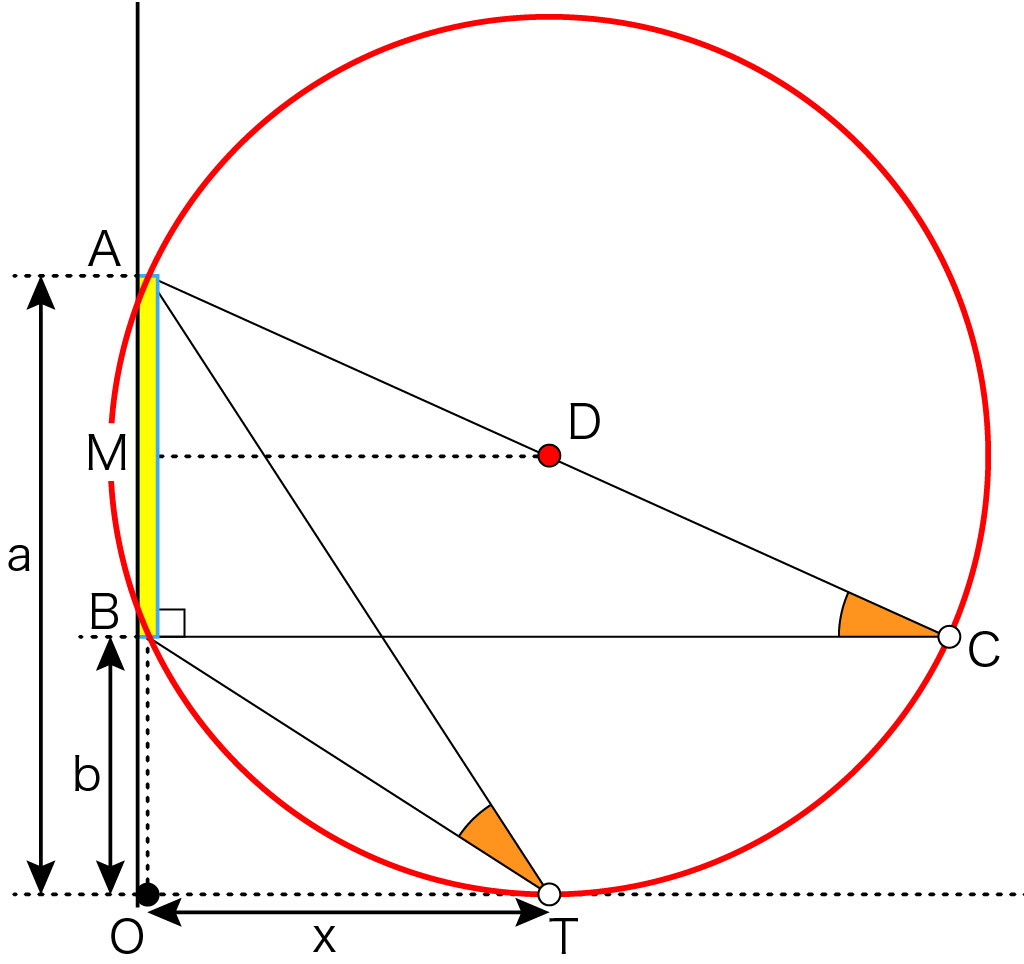
円上の点で,\(\text{B}\)と同じ高さの点を\(\text{C}\)とし,円の中心を\(\text{D}\)とします。\(\text{D}\)は\(\text{T}\)の真上にあります。
\(\text{A}\)と\(\text{B}\)の中点を\(\text{M}\)とすると,\(\text{M}\)は\(\text{D}\)と同じ高さで\(\text{OM}=\frac{(a+b)}{2}\)です。これは\(\text{DT}\)に等しく円の半径に他なりません。半径を\(r\)とします。
\(\text{MD}\)は\(x\)に等しいので,直角三角形\(\text{AMD}\)に対してピタゴラスの定理を適用すると,
\(r^2=x^2+\text{AM}^2\)
です。\(\text{AM}=\frac{(a-b)}{2}\)ですから,上の式を解いて,
\(x=\sqrt{ab}\)
を得ます。
よって,絵画が大きく,高い所に掲げてある場合,遠くから見た方がよく見えそうなことは,直観的に(定性的に)わかりますが,絵画の上端と下端の床からのそれぞれの高さの相乗平均だけ遠くに離れるのがベストであることが(定量的に)わかりました。
(後編では,以上の話を応用して,ラグビーのコンバージョンキックする位置について,さらに深掘りした考察をします。)
1970年東京生まれ。早稲田大学理工学部数学科卒業。東京大学大学院数理科学研究科数理科学専攻博士課程修了。現在,明治大学理工学部数学科専任教授。博士(数理科学)。専門は応用数理,特に界面現象の数理解析。実験を採り入れた数学の講義で定評がある。
| 著書: | 『実験数学読本』①・②・③ (日本評論社),『次元解析入門』,『界面現象と曲線の微積分』,『動く曲線の数値計算』(以上共立出版),『大学数学の教則』(ちくま学芸文庫),『公式は覚えないといけないの?』(ちくまプリマー新書),他。 |
その他のコンテンツ
