特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。

今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

令和6年度全国学力・学習状況調査の結果を生かした授業づくり③

Q　令和6年度全国学力・学習状況調査問題に図形の証明についての問題が出題されました。図形の証明について調査結果を活かした授業づくりのポイントを教えてください。

Ａ　全国学力・学習状況調査問題の複数設問からなる問題は、問題解決の文脈が大切にされています。ここでは記述式問題も設定されています。今回は領域B図形における大問を取り上げ、調査結果を生かした授業づくりを考えてみましょう。

　前回までは、令和6年度全国学力・学習状況調査結果を生かした指導の改善・充実について領域C関数の問題を例に考えました。特に「知識及び技能」に焦点を当て、調査結果を生かした授業づくりをお伝えしました。
　今回は、令和6年度全国学力・学習状況調査問題大問９についてです。解説資料によると大問９は図形の性質を考察する場面として、下の２つの趣旨が設定されています。今回は、①について考えてていきます。

① 予想した事柄が成り立つことを論理的に考察し表現すること

② 問題解決の過程や結果を振り返って新たな性質を見いだす

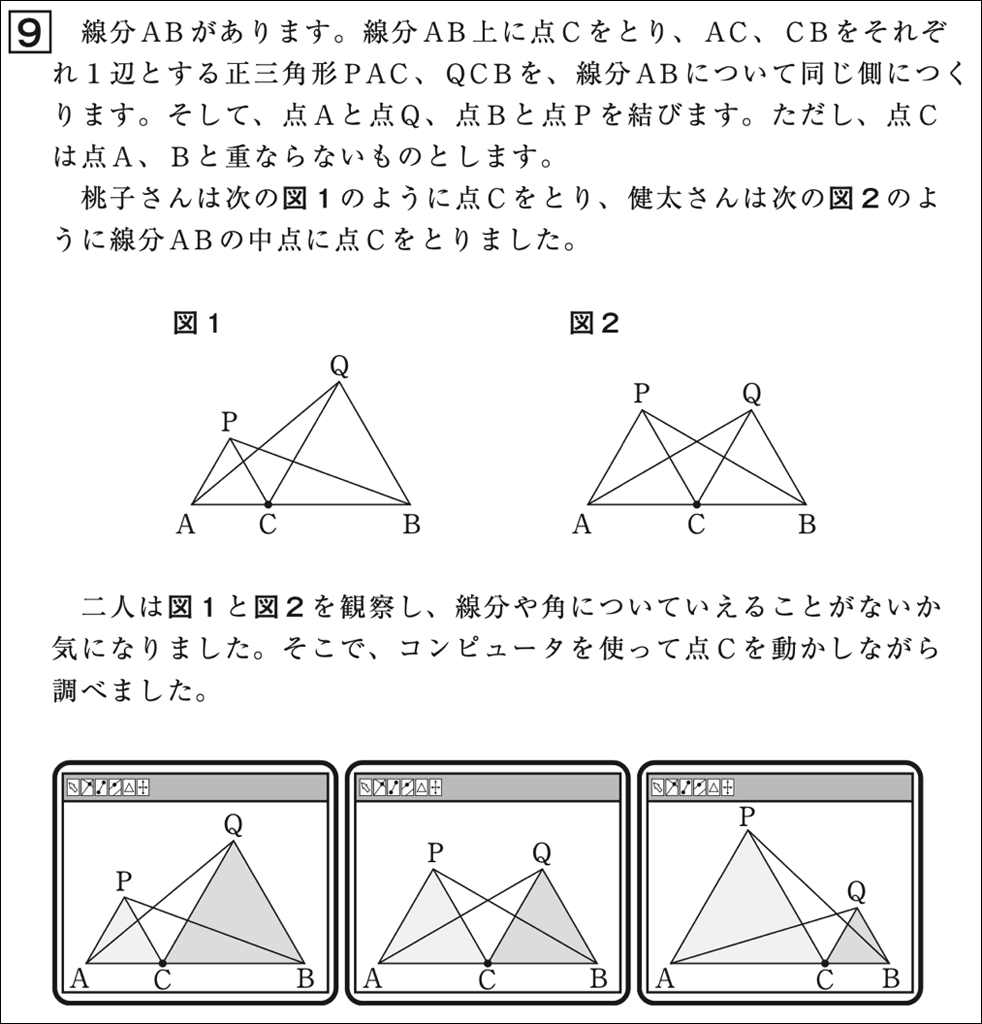
令和6年度全国学力・学習状況調査問題大問９冒頭について

□中学校数学大問９（１）について

　本設問は、第２学年における内容で、筋道を立てて考え、証明することができるかどうかをみるものです。「三角形の合同の関係を利用した図形の性質の証明」の問題は、平成29年度調査以来の出題です。そのときの正答率は45.0％（無解答率19.8％）で、数学的に考えることに課題があると報告されました。今年度の問題では、下のように図において\(\text{AQ=PB}\)となることを、\(\triangle \text{QAC}\)と\(\triangle \text{BPC}\)の２つの三角形の合同の関係に着目し、それを示し説明します。解答形式は根拠とそれによって導かれる結論を明示する「理由の説明」です。また、評価の観点は「思考・判断・表現」です。

令和6年度全国学力・学習状況調査問題大問９（１）

　実際の解答状況について報告書をみてみると、正答率は26.5％と低く、さらに無解答率は33.2％となり、指導の改善が必要であることが伺えます。

□書いた証明をどのように評価するかを明確にすること

　「筋道を立てて考え、証明すること」を評価するとき、特に記録に残すための評価を考える際には多くの先生が生徒の実際の証明の記述で判断すると思います。例えば、定期テストはその一つの評価場面です。証明を書くことができるかどうかの正誤のフィードバックする際に、生徒が書いた証明をどのようにみるとよいでしょうか。全国学力・学習状況調査での正答の条件は下のようになっています。正答の条件である(a)〜(d)について、根拠と併せた記述を求めています。「(a)、(b)が成り立つ根拠として正三角形の特徴より対応する辺に相等関係があること」、「（d）が成り立つ根拠として (a)〜(c)が三角形の合同条件を成り立たせる要素を取り上げ、三角形の合同条件である「二辺とその間の角がそれぞれ等しい」を根拠として示すこと」など具体的な根拠を明示して結論を述べているかどうかをみとり、評価とします。
　生徒が“証明を書くことができている”かどうかについて評価するとき、成り立つと予想した事柄について、根拠と結論を明記し、筋道を立てて考えたことを表現することができたかどうか確認する必要があるのですね。

□生徒のつまずきの想定とそれを乗り越えるための手立てを用意すること

　本問は、正答率が低いだけでなく、無解答率が高いという状況にあり、深刻です。図形の証明について学習する第２学年では、書くことに拘らずに証明の方針や構想を考えることも大切です。このことについては【#14】で取り上げていましたので、そちらをご覧ください。本問におけるつまずきについて、報告書に記載されている解答類型を確認します。注目すべき解答類型とその反応率については、下の３つです。
　□解答類型５：仮定として、\(\text{AQ=PB}\)を用いているもの。【反応率 9.1％】
　□解答類型８：(a)、(b)について記述しているもの。【反応率 9.6％】
　解答類型５については、証明したい事柄の結論について捉えに課題があります。授業では証明の方針（【#14】を参照）を考えることを授業場面に取り入れ、生徒自ら証明しようとしている事柄について確認できるようにしましょう。解答類型８については、正答の条件である(c)、(d)が記述できなかったということになりますが、おそらく「\(\angle \text{ACQ}=\angle \text{PCB}\)」になる根拠を記述できなかったのではないかと予想されます。では、このような生徒の困り感について考えてみましょう。
　三角形の合同について\(\triangle \text{QAC}\)と\(\triangle \text{BPC}\)をみてみると、互いの三角形に重なりがみられ、対応する辺や角の位置及びその関係について捉えが難しいことが考えられます。このつまずきを解消するために、それぞれの三角形をみやすく整理するなどの工夫が必要です。例えば、下のように、\(\triangle \text{QAC}\)と\(\triangle \text{BPC}\)の２つの三角形を抜き出して考えることができます。

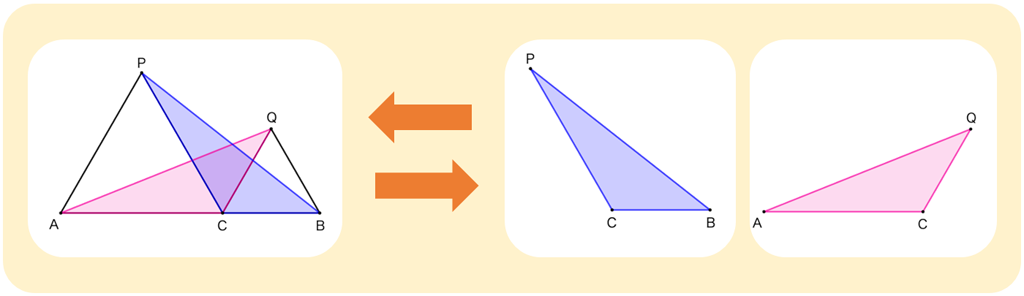
　上のように図を抜き出して分けて考えることで、対応する\(\angle \text{ACQ}\)と\(\angle \text{PCB}\)の関係に着目することができるようになります。\(\angle \text{ACQ}\)と\(\angle \text{PCB}\)それぞれの角の構成を考え、２つの角の共有部分（\(\angle \text{PCQ}=60^{ \circ }\)）の存在に気づき、\(\angle \text{ACP}=\angle \text{QCB}=60^{ \circ }\)になることから\(\angle \text{ACQ}\)が\(\angle \text{PCB}\)が\(120^{ \circ }\)になり相等関係にあると捉えると考えられます。授業では、生徒が図を整理して考える場面を設定するなどして、図形やその関係に着目して考えるといった数学的な見方・考え方が鍛えていくことが大切です。実際には生徒の状況に応じて、２つの三角形の対応する辺や角の関係を捉えることができるようにするためには、どのようにすればよいかを問いかけたり、助言したりするとよいでしょう。
　実は、平成29年度調査において同じような傾向があることが報告されています。その問題は下のとおりです。

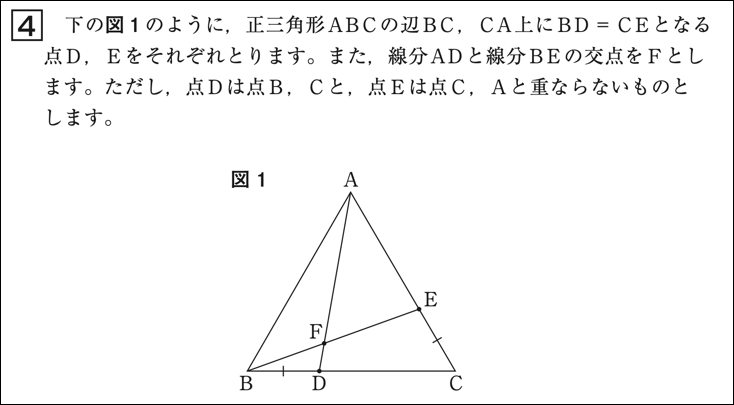
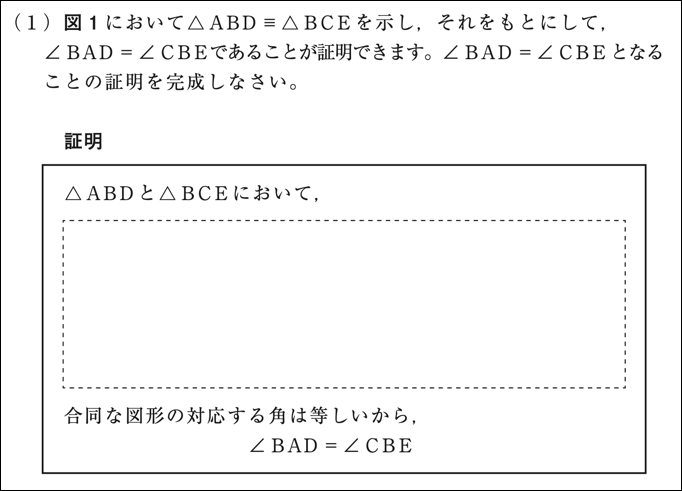
平成29年度全国学力・学習状況調査問題B大問４（１）

　この問題では\(\angle \text{BAD}=\angle \text{CBE}\)が成り立つことを\(\triangle \text{ABD}\)と\(\triangle \text{BCE}\)の合同の関係を利用して示すのですが、当時、\(\angle \text{ABD}=\angle \text{BCE}\)が等しくなること及びその根拠について説明できなかったことが課題として報告されました。\(\triangle \text{ABD}\)と\(\triangle \text{BCE}\)が重なりがあることから、それらを抜き出した図を基に対応する辺や角を確認する場面を設定することが大切であるといわれてきたのです。
　図形の証明は書くことに拘らず、筋道を立てて考えることを表現することに力点をおいた指導が期待されるが、生徒が図における辺や角の関係を捉えることができず、証明を書くことができないことを受け止め、生徒の状況を踏まえた上で、具体的な指導改善を努めることが大切です。

※参考資料　

• 　平成29年度全国学力・学習状況調査解説資料中学校数学（国立教育政策研究所）
• 　平成29年度全国学力・学習状況調査報告書中学校数学（国立教育政策研究所）
• 　令和6年度全国学力・学習状況調査解説資料中学校数学（国立教育政策研究所）
• 　令和6年度全国学力・学習状況調査報告書中学校数学（国立教育政策研究所）

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。