今週の算数・数学フォト
- TOP
- 今週の算数・数学フォト
- 湖の底の、7万年の記録

福井県年縞博物館
そうたです。ここは「福井県年縞(ねんこう)博物館」。さっき外から建物を見て、ずいぶん細長くて不思議だと思ったんだ。おおもとは、この廊下だったみたいだね。なんの展示だろう。なになに、 「水月湖年縞 7万年ギャラリー」?

この細かい縞模様が、はるか向こうまで45mも続くよ。この模様が「年縞」。すぐそこの水月湖(すいげつこ)という湖の底から掘り出した、地層なんだ。展示されているのはその現物だから、本当に不思議な気持ちになるよね。
45mも続くこのシマシマが、タテ向きに湖の底に沈んでいたということ? ずいぶん細かいよ。ヨコに展示してあるせいもあるけど、まるでバーコード。

おおっ。「バーコード」とはいい視点だよ、そうたさん。どちらも白黒のラインでできているしね。この年縞の黒っぽい部分は、春から秋にかけて積もるプランクトンの死骸や珪藻といった有機物だよ。秋の終わりから冬にかけては、黄砂などの無機物が積もって白い層になる。つまり黒と白のセットで、1年。平均すると1年分の年縞の厚さは約0.7mmだって。
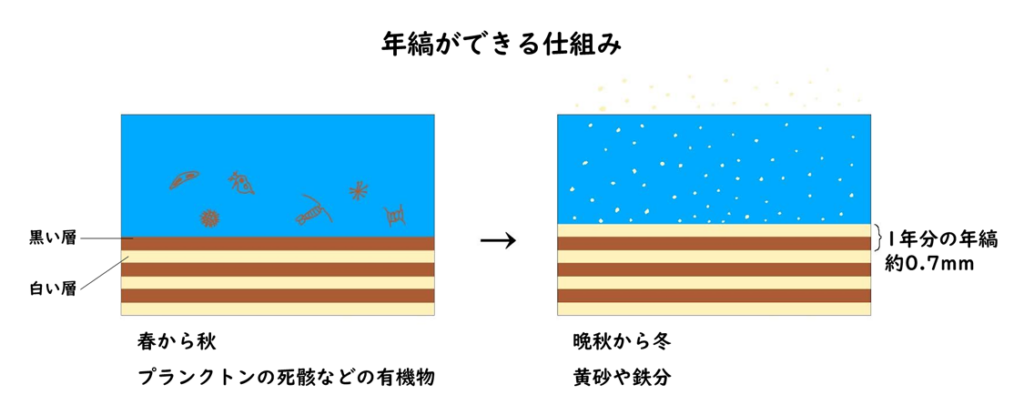
45mは45,000mmだから、これを0.7mmでわると
\(45000\div 0.7 \fallingdotseq 64286\)
なるほど。だいたい64,000年分といえるかな?
うん、計算は合っているよ。火山の噴火や地震があった年には層の厚さが変わることもあるから、実際には1層ずつきちんと数えて、7万年分の地層があるとわかったんだよ。
1層ずつ数えたの!? 7万年っていうことは、黒と白の2本で14万本か。途方もないね。そもそも、湖の底を、地層をくずさないように45mも掘るなんて。想像もつかないよ。
そりゃもう、大変なプロジェクトだったんだ。行われたのは、湖の底にパイプをさして土を採る「ボーリング」という方法。採り出した土は「コア」と呼ばれるんだけど、1回のボーリングで採れるコアの深さはたった1mだから、パイプを引き抜いた所に次のパイプを入れてさらに深い層を採取していくんだけど……どうしても、継ぎ目の部分の年縞は欠けてしまう。
うーん。確かに、採り出した土のはしっこが少し欠けただけで、地層の全体像はつかめなくなるよね。
そこで、4カ所の穴でボーリングを進めたんだ。それぞれのコアを突き合わせて比べることで、ついに全長45mの完全な年縞を採取することに成功。ここでヒントになったのが、さっきそうたさんが言った「バーコード」だったんだよ。例えば、ある年には豪雨で洪水が起きた。すると、その年の年縞の幅は、たくさんの堆積物のために広くなる。もちろん火山の噴火や地震でも、年縞の幅はさまざまに変化する。
なるほど。4本を並べて、パズルみたいに合わせていったんだね!
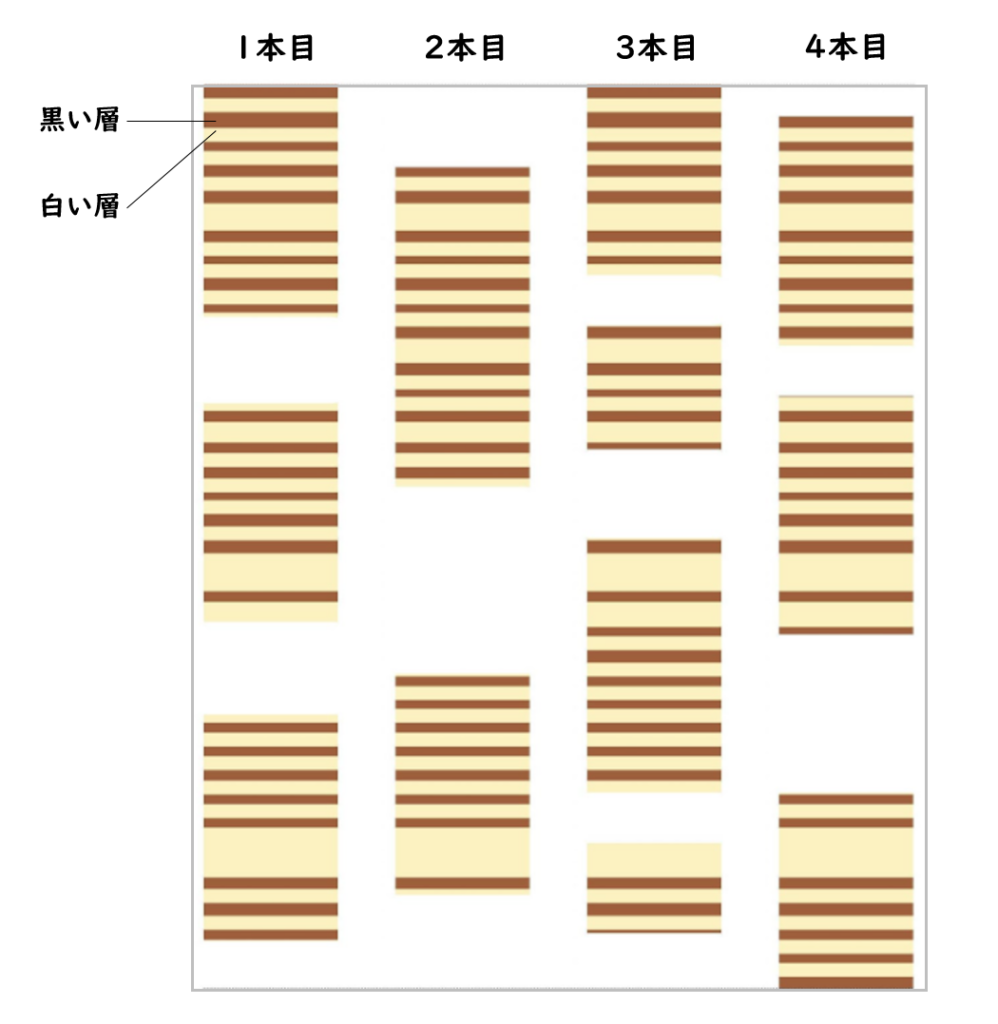
その通り。7万年分もの完全な年縞が採取できているのは、世界でも、ここ水月湖だけなんだよ。①大きな川が流れ込まない ②湖底に生き物がいない ③長い年月に渡り、湖底が少しずつ沈み続けてきた という3つの条件が重なって、積もり続けた地層が保たれてきた。まさに「奇跡の湖」だね。
なるほど。すごく貴重なことはわかった。ところで、そもそも年縞って何の役に立つの?
そう、そこが大事だよね! 「放射性炭素年代測定」という方法は知ってる? 古い地層から植物が見つかったとき、そこに含まれる「炭素14」という放射性物質の量を調べることで、その植物がおよそ何年前に枯れたかがわかるんだ。この方法による測定値と実際の年代の関係を正確に調べるために、この年縞が使われるんだよ。
へえええ。ずいぶん、具体的な話になってきた。
なにしろこの「7万年ギャラリー」では、最後の氷期が終わったときの地層(1950年を基準にした11,653 \(\pm\) 99年前)や、今の富士山ができる以前の古富士の火山灰(1950年基準で43,713 \(\pm\) 300年前)が、ほぼ正確に記録されている。考古学や地質学における、「世界標準のものさし」の元にもなっているんだよ。
43,713年前!? すごく正確にわかるんだね。年縞の長さと時間は「関数」と考えられるね。数学の考え方って、他のいろいろな学問にも深く関わってくるんだね。
*福井県年縞博物館/福井県三方上中郡若狭町。三方五湖のひとつである水月湖で発見された年縞の展示と研究を行う。2018年開館。
*写真提供:福井県年縞博物館
*イラスト:大野寛武先生制作
〒919-1331 福井県三方上中郡若狭町鳥浜
その他のコンテンツ
