特集記事（小中学校）

相模原市立相武台中学校
加藤光顕先生

　今回は、3年で学習する2次方程式の実践で活用したデジタル教科書の有効な方法をご紹介します。

Dマークコンテンツ「点が動くようすを見てみよう」はこちら

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。

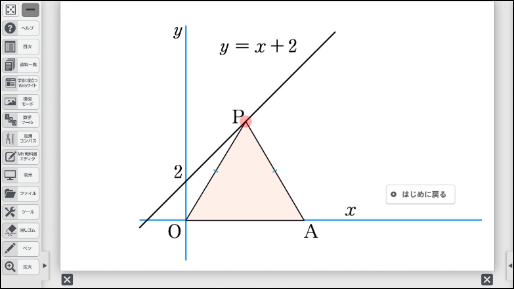
①アニメーションで面積の変化のようすを視覚化する

□単元：3章　2次方程式　　□内容：p.89　動点が作る三角形の面積　　□学年：中学3年

　2次方程式の利用において、動点の問題を苦手とする生徒は多くいます。苦手とする生徒からは、「なぜ点が動く必要があるのか」という質問を受けることがあります。
　そのようなこともあって、私は動点の問題を扱う際には、まず生徒に「点が動くことで、何が変わるだろうか」「逆に点が動かなければどうなるだろうか」のようなやりとりをするように心がけています。そうすると、生徒は、点が動くことで長さの変化があることに気づき、長さの変化と面積との関係に注目します。

長さにともなって面積が決まる。これは次の章「関数 \(y=ax^2\) 」にもつながる大切なステップだと考えています。中学2年の3章1次関数でも動点の問題を扱いましたが（参考記事：クロームブック活用術 実践⑫）、今回は動く点がさらに1つ増えることで、より複雑な課題となっています。ここでもデジタル教科書のシミュレーションを活用することで、面積の変化のようすを視覚化することができるため、多くの生徒が課題に取り組みやすくなることでしょう。実際の解法は、次のようになります。

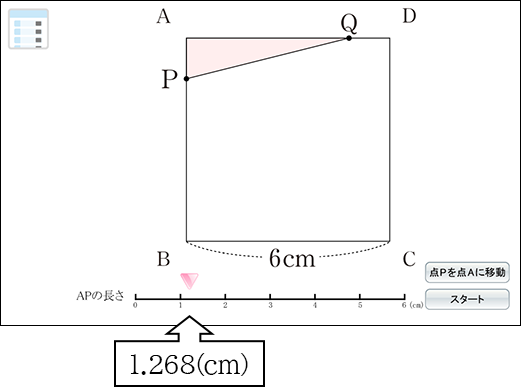
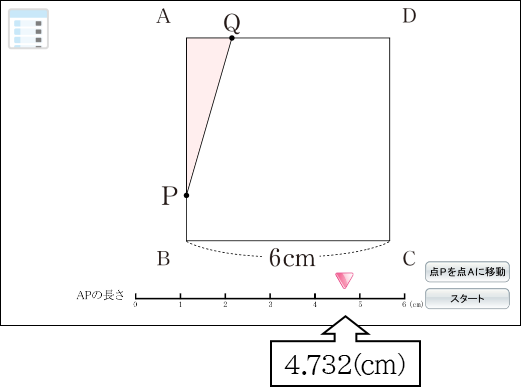
　ここで、生徒のなかには、方程式の意味は理解できていても解に根号が入ることによって混乱してしまう生徒もいたりします。そのようなときには、\(3\pm \sqrt{3}\) の近似値をそれぞれ求めさせ、実際の長さがどれくらいの長さなのかをイメージさせるとよいでしょう。

\(　　　3+\sqrt{3}\fallingdotseq 3+1.732=4.732 \text{(cm)}\)
\(　　　3-\sqrt{3}\fallingdotseq 3-1.732=1.268 \text{(cm)}\)

　この値をもとに、Dマークコンテンツ「点が動くようすを見てみよう」を使って、\(\triangle \text{APQ}\) の面積が3cm²になる図を示すことで、多くの生徒が理解できるようになりました。

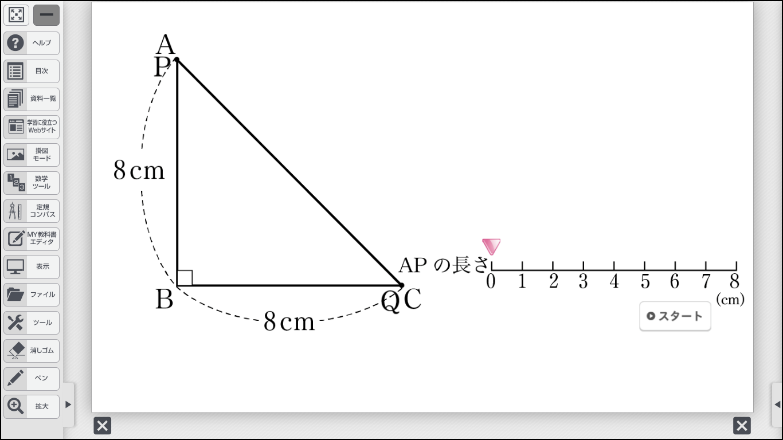
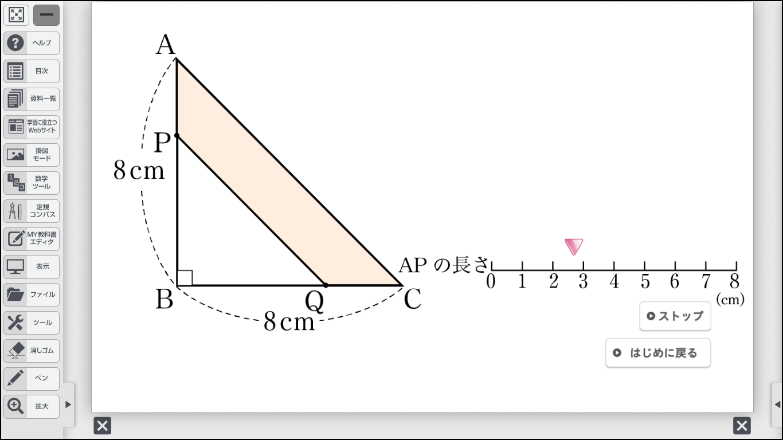
□単元：3章　2次方程式　　□内容：p.89　動点が作る正方形の面積　　□学年：中学3年

　次の課題も、デジタル教科書のシミュレーションを活用することで、辺 \(\text{AP}\) の長さを変えることで図形が変化するようすを確認することができます。

課題
長さが8cmの線分 \(\text{AB}\) 上を、点 \(\text{P}\) が \(\text{A}\) を出発して\(\text{B}\) まで動きます。
\(\text{AP}\)、\(\text{PB}\) をそれぞれ1辺とする正方形の面積の和が36cm²になるのは、点 \(\text{P}\) が \(\text{A}\) から何cm動いたときですか。

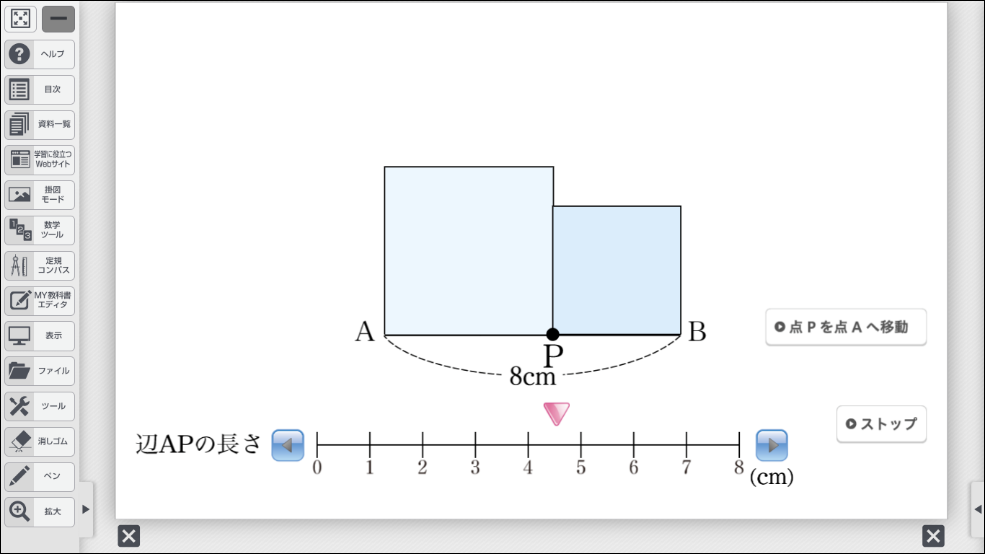
　生徒は、辺 \(\text{AP}\) の長さを変えることで、左右の四角形の大きさが変わることに気づき、辺 \(\text{AP}\) の長さが変数になることを容易に理解できるようになるはずです。

□単元：3章　2次方程式　　□内容：p.90～p.91　動点が作る面積　　□学年：中学3年

　3章の総合問題となる「章の問題」でも、動点を扱った問題が2つあります。ここでもデジタル教科書のシミュレーションを活用することで、点が動くとどのように面積が変化するのかを確かめることができます。2年で既習した1次関数と面積との関係についても視覚化することができるので、問題の概要を把握したり、解法を考えたりするうえでも非常に有効に働くことでしょう。

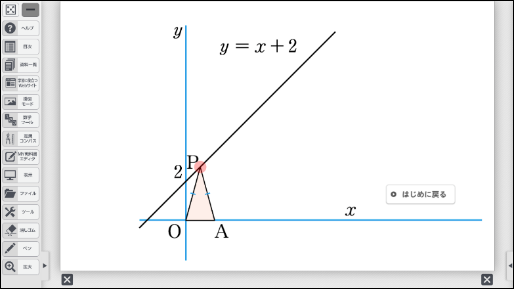
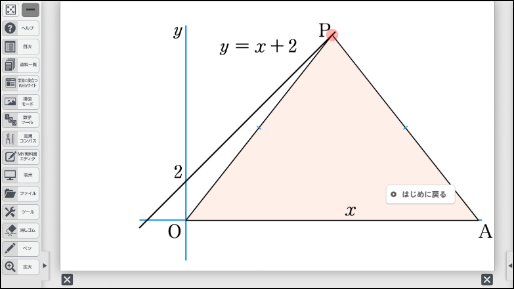
③まとめ

　今回は、動点の問題を考える際に、問題の概要を理解したり、解法を考えたりするうえでのデジタルコンテンツの有効性について紹介しました。特に動点の問題は、問題文や条件の複雑さから、問題内容を理解するところからつまずきやすいです。そのことから、問題文を読むだけで「意味がわからない」「やる気が起きない」「解法の筋道が見えない」と思う生徒も少なくありません。そのような生徒には、まず問題の概要をつかませることが大切です。文章ではイメージが湧かなくても、コンテンツで視覚化することで、問題の概要もつかみやすくなるはずです。問題の概要をつかむことで、生徒のやる気が復活し、それにともなって解法の筋道に気づく生徒も出てくることでしょう。ぜひ、試してみてください。