特集記事(小中学校)
- TOP
- 特集記事(小中学校)
- 【ICT教育のイマ】クロームブック活用術 実践⑫~…
中学校
2022.10.14
【ICT教育のイマ】クロームブック活用術 実践⑫~Dマークコンテンツ/操作編~
相模原市立相武台中学校
加藤光顕先生
今回は、Dマークコンテンツを活用した生徒の学び方(個別最適化と理解支援)で有効な方法をご紹介します。

①動点という題材から、長さの変化が面積にどう影響するか、関数と捉えることを学ぶ。
□単元:3章 1次関数 □内容:動点と面積の問題(p.88) □学年:中学2年生
「なぜ、点が動く必要があるのですか?」、生徒からはよくこんな質問を受けます。
動点の問題を苦手とする生徒の不満もあるのかもしれませんが、それでも動点という問題をなぜこの単元で扱うのかということについては、授業者としてしっかり押さえなくてはならないとも思います。
私は、まず生徒のそんな疑問を生徒自身に考えさせることから授業を始めます。「点が動くことで、何が変わる?」「逆に点が動かなければどうなる?」。そうすると、生徒は、点が動くことで長さの変化があることに気づき、そして面積と関係があることに注目します。長さにともなって面積が決まる。これぞまさに関数となる。そこから具体的に長さと面積がどう関係しているのかを探ることにしています。
とはいっても動点の問題は、点が辺上のどこにあるかによって場合分けをする必要があり、理解に苦しむ生徒も少なくありません。そのときに有効なのが、Dマークコンテンツ「動点と面積の関係を考えよう」です。シミュレーションで点を動かし、面積の変化を可視化することで問題の意味を理解することに繋がります。また点PがAから動いた長さを設定することができ、その場合の面積を確認することができます。さらに、点Pの軌跡が赤色になることで、\(x\)cmがどの部分の長さの合計にあたるのかが明確になりDPの長さを考える際に一役買うことでしょう。
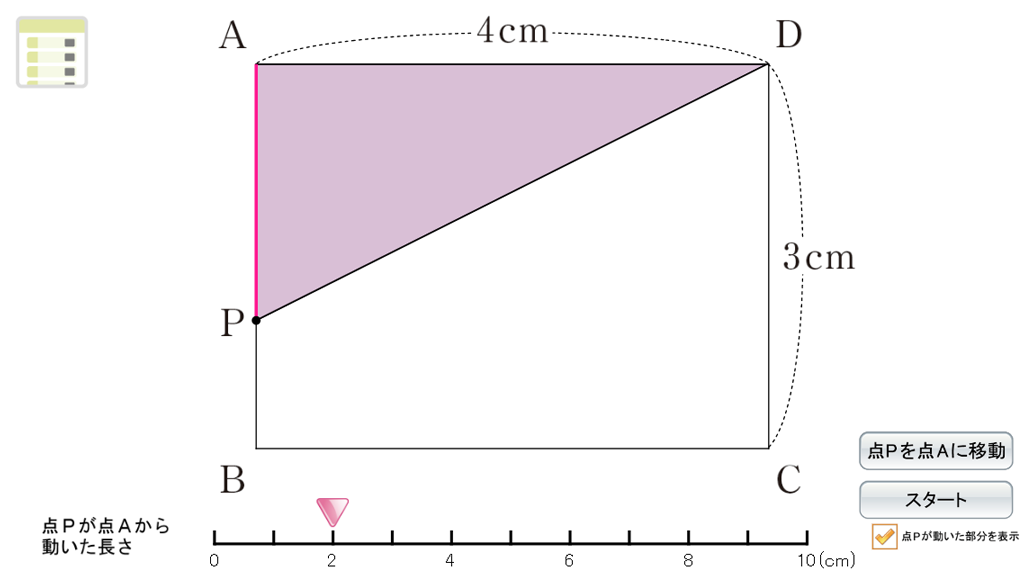
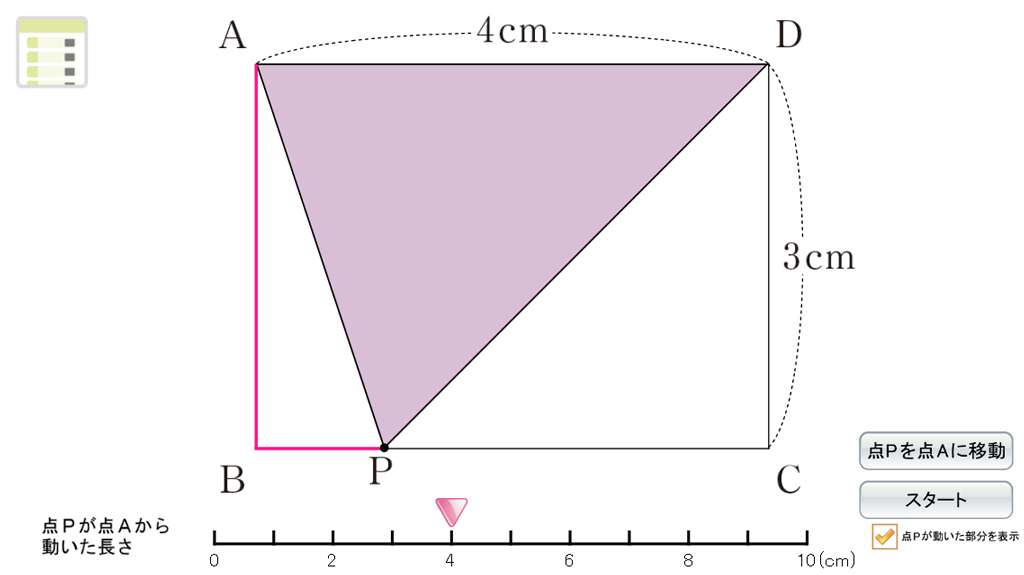
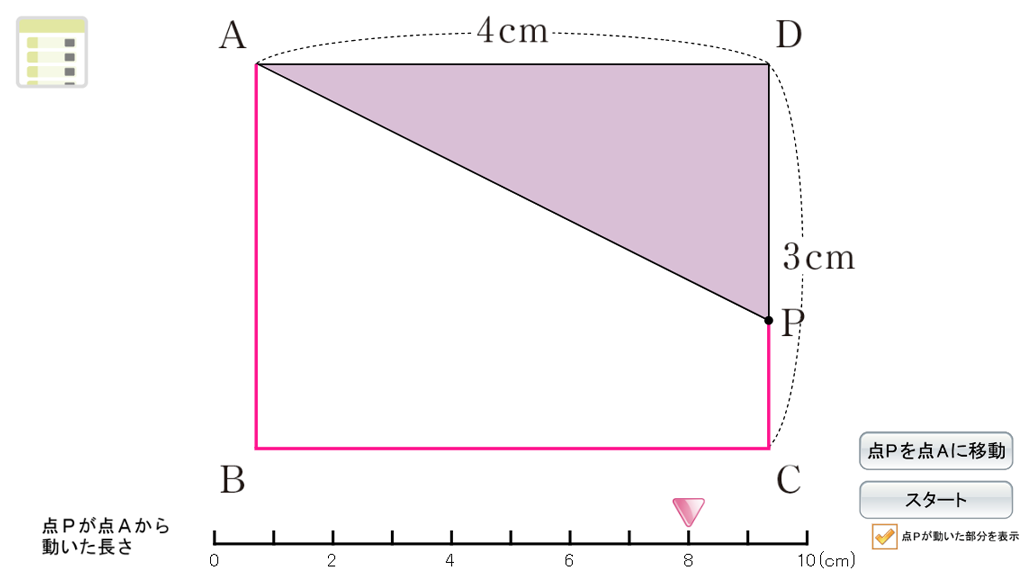
三角形の面積は、底辺\(\times\)高さ\(\div\)2で求められます。ADを底辺と見ると高さが変化していることに気づき、面積はその高さの変化によって決まること、すなわち関数になることに気づかせます。そして、△ADPの面積は点PがAB上では面積が増加し、BC上では一定となり、CD上では面積が減少すること、そして式とグラフとの関連(傾きと切片)を理解できることがゴールです。そのための手助けとして、このコンテンツは生徒にとって重要なツールとなることでしょう。
②ワークシート生徒の解答例
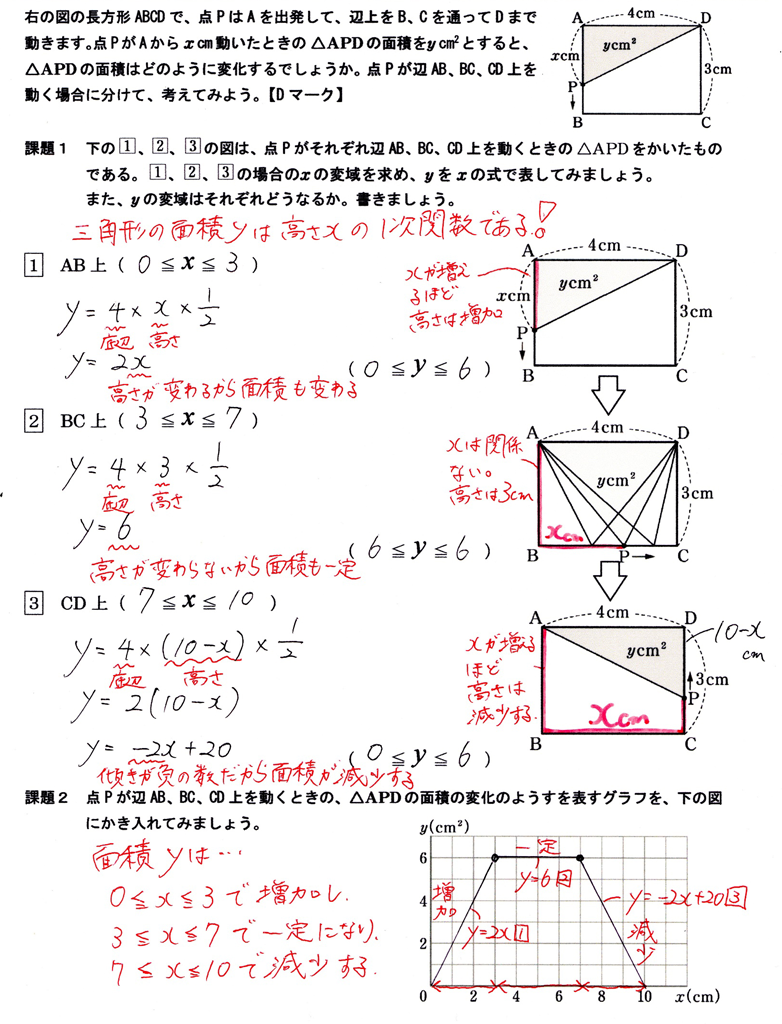
その他のコンテンツ
