特集記事(小中学校)
- TOP
- 特集記事(小中学校)
- 【ICT教育のイマ】クロームブック活用術 実践55…
中学校
2024.05.28
【ICT教育のイマ】クロームブック活用術 実践55~デジタル教科書(3年 2次方程式①)~
相模原市立相武台中学校
加藤光顕先生
今回は、3年で学習する2次方程式の実践で活用したデジタル教科書の有効な方法をご紹介します。

①本題に入る前のステップ(しかけ)がイメージ力を高める
□単元:3章 2次方程式 □内容:p.71 2次方程式の立式 □学年:中学3年
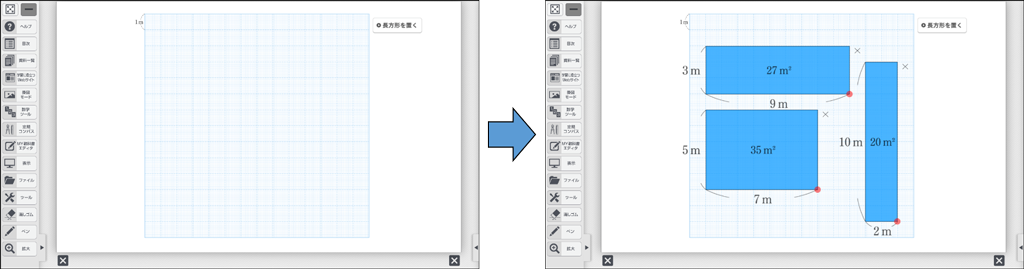
2次方程式の導入では、畑を長方形として捉え、周の長さが24mの長方形の面積を教材として扱っています。はじめに、生徒に周の長さが24mの長方形をたくさんかかせます。その際に、デジタル教科書のシミュレーションを活用すると、簡単に長方形をつくったり消したりすることができるため非常に便利です。
最終的な目的は、与えられた面積から縦と横の長さを求めるための方程式を立式することなので、これぐらい作業が手軽に行えると、時間もかからずスムーズに次のステップに進むことができるでしょう。

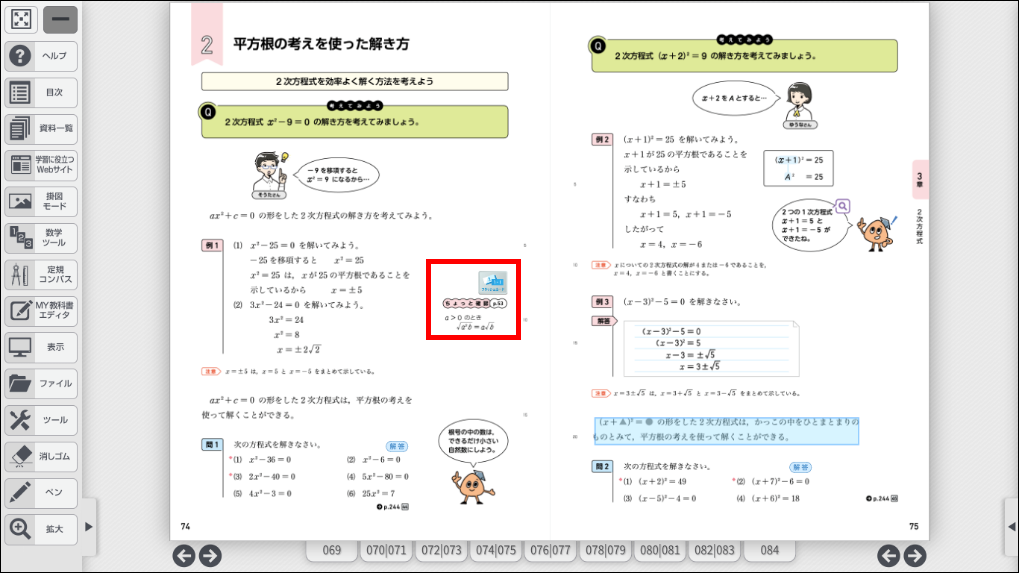
□単元:3章 2次方程式 □内容:p.74 平方根を使用する2次方程式 □学年:中学3年
平方根の考えを使った2次方程式の解き方では、例えば \(3x^2-24=0\) を解く問題だと
\(3x^2-24=0\)
\( \ \ 3x^2=24\)
\( \ x^2=8\)
\( \ \ \ x=\pm \sqrt{8}\)
\( \ \ \ x=\pm 2\sqrt{2}\)
となりますが、このとき \(x=\pm \sqrt{8}\) から \(x=\pm 2\sqrt{2}\) にする方法を忘れてしまう生徒がいたりします。そのようなときには、「ちょっと確認」のページで復習することができます。
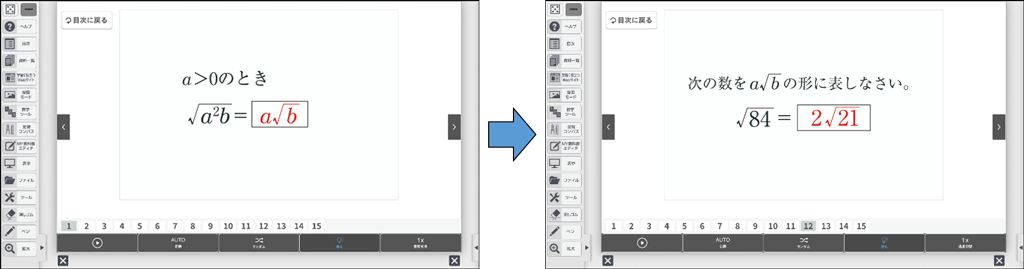
デジタル教科書のフラッシュカードを活用すれば、それぞれの問題をランダムに表示することができます。さらに「自動」機能を使うことで、数式と答えが自動で表示されるので、自身の理解や定着度を確認することができます。また、表示されるスピードも変えることができるので、自身の状況に合わせて調節することもできます。数分で実践できるため、文字通りちょっと確認をすることで円滑な計算につなげることができるでしょう。
□単元:3章 2次方程式 □内容:p.76 乗法公式 □学年:中学3年
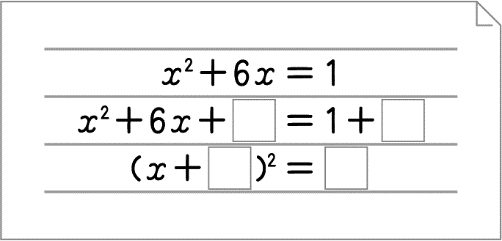
2次方程式 \(x^2+6x-1=0\) の解き方を考える場合、\((x+▲)^2=●\) の形に変形する必要があります。
このとき乗法公式2を利用する必要があり、図のように穴埋め形式で考えさせるとわかりやすくなります。
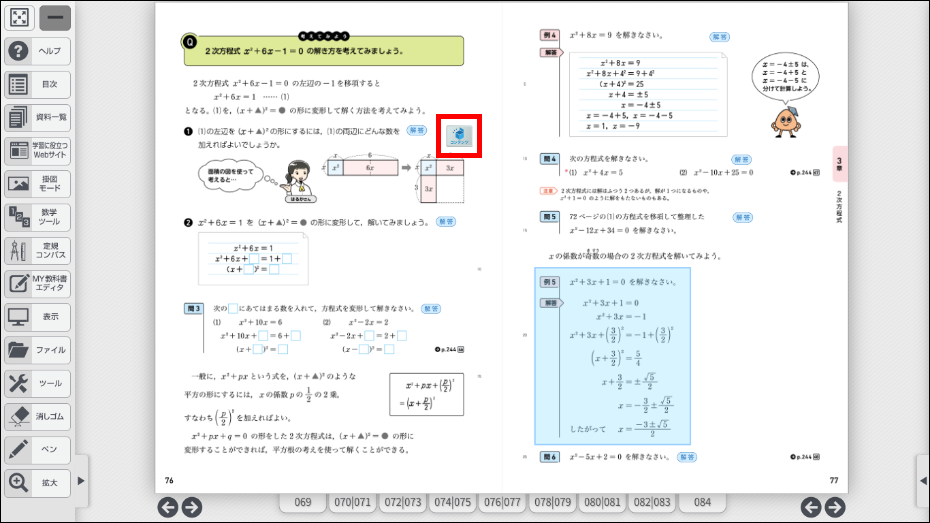
さらに理解を深めるためには、図で確認することが重要です。デジタル教科書にあるアニメーションを活用すると効果的です。実際に生徒からも「わかりやすい」「イメージが持てた」などの声がいくつも挙がりました。
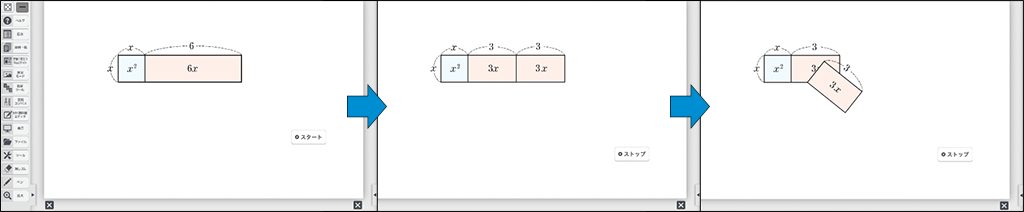
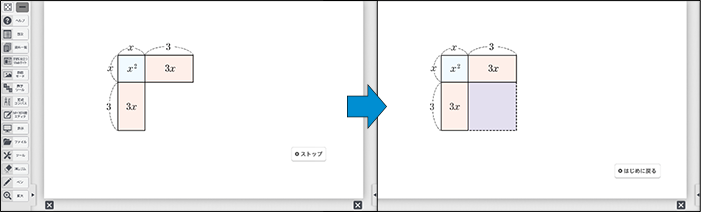
②まとめ
今回は、本題に入る前のステップとして、デジタル教科書の活用方法を紹介しました。このステップを入れることで、生徒のイメージ力をより高めることができます。生徒のイメージ力を高めることは、学習意欲やその後の理解度に大きく影響すると私は考えています。しかし、忙しい現場では毎回の授業でそのための準備をすることは難しく、継続しづらい状況もあるかと思います。デジタル教科書なら事前準備は全く必要ありません。クロームブックが普及している環境を有効に活用することで、ちょっとしたしかけを日々の授業に取り入れてみるのはいかがでしょうか。
その他のコンテンツ
