中学校
2023.12.05
【ICT教育のイマ】クロームブック活用術 実践㊲～デジタル教科書／操作編（3年 円⑤）～
相模原市立相武台中学校
加藤光顕先生
今回は、3年円の円周角の定理の学習で活用したデジタル教科書の有効な方法をご紹介します。
①作図方法を理解し、その目的を説明する
□単元：6章 円 □内容：p.178～p.179 円周角の定理の利用 □学年：中学3年
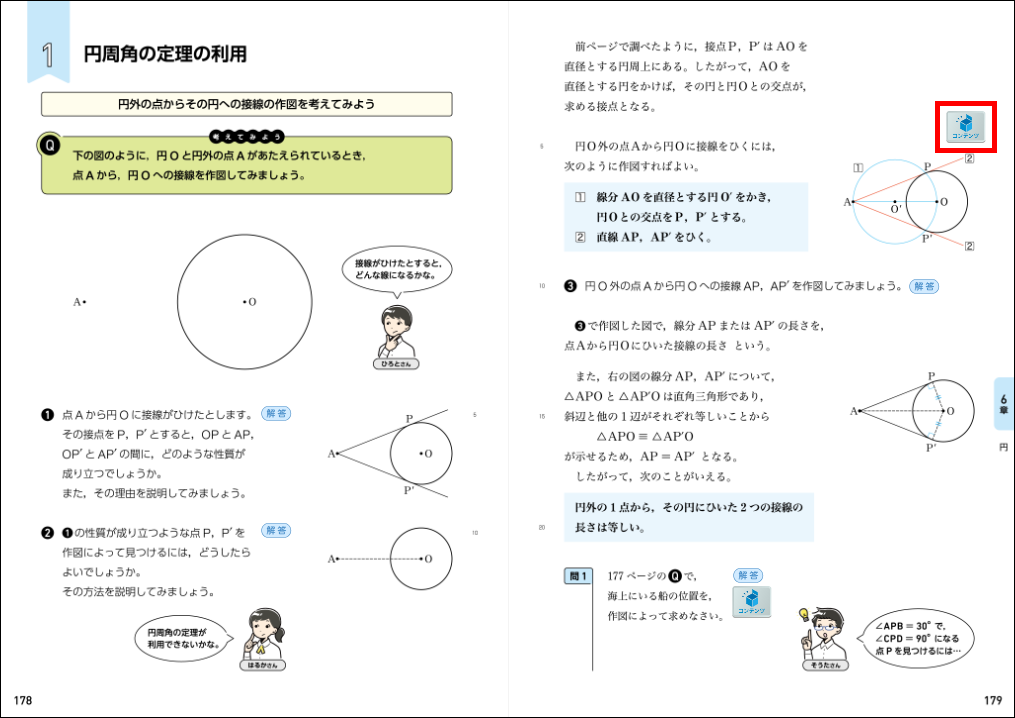
教科書p.178では、「円外の1点から、その円にひいた2つの接線の長さは等しい」ことを学びます。ここでは円外の1点を \(\text{A}\) とし、円 \(\text{O}\) への2つの接線を考えます。中学1年で学習した接線の作図ではなく、次の手順で生徒に作図させます。
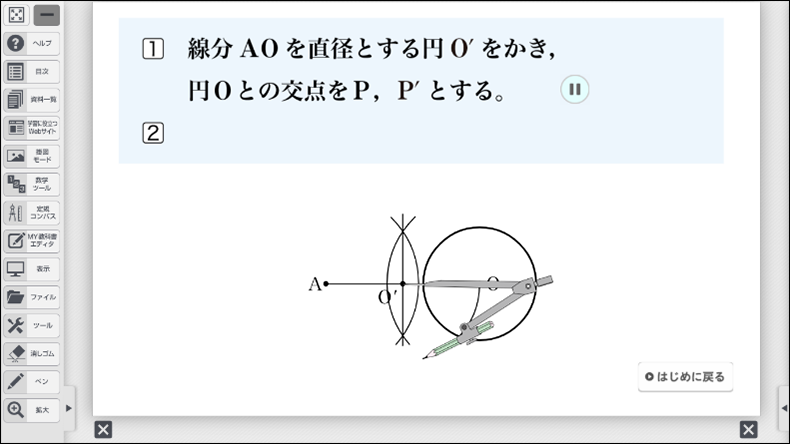
- 点\(\text{A}\)と点 \(\text{O}\) を線で結び、線分 \(\text{AO}\) の垂直二等分線を作図する。
- 垂直二等分線の中点を\(\text{O´}\) とする。
- 半径 \(\text{AO´}\) となる円 \(\text{O´}\) を作図する。
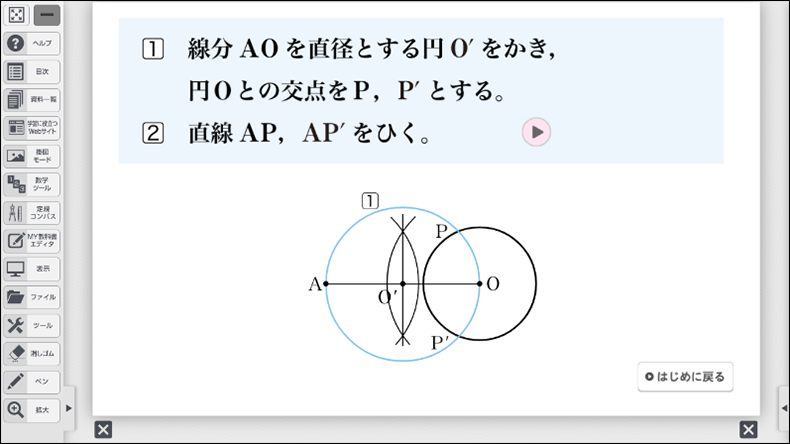
- 円 \(\text{O}\) と円 \(\text{O´}\) との交点を \(\text{P}\)、\(\text{P´}\) とする。
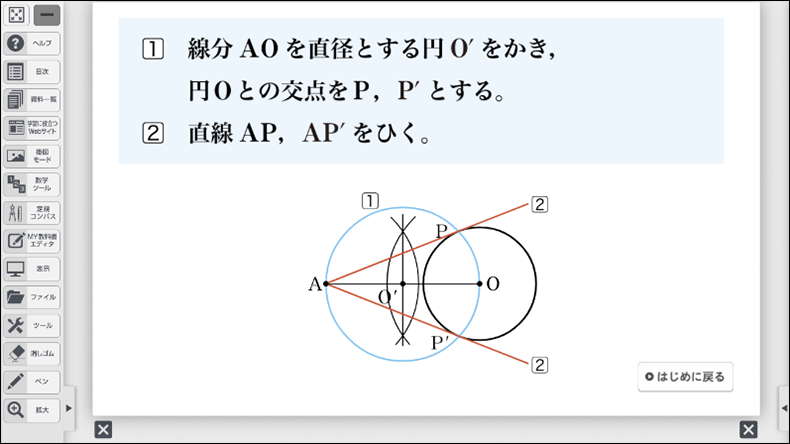
- 点 \(\text{A}\) と\(\text{P}\)、点 \(\text{A}\) と \(\text{P´}\) をそれぞれ直線で結ぶ。\(\text{AP}\) と \(\text{AP´}\) がそれぞれ円 \(\text{O}\) への接線となる。
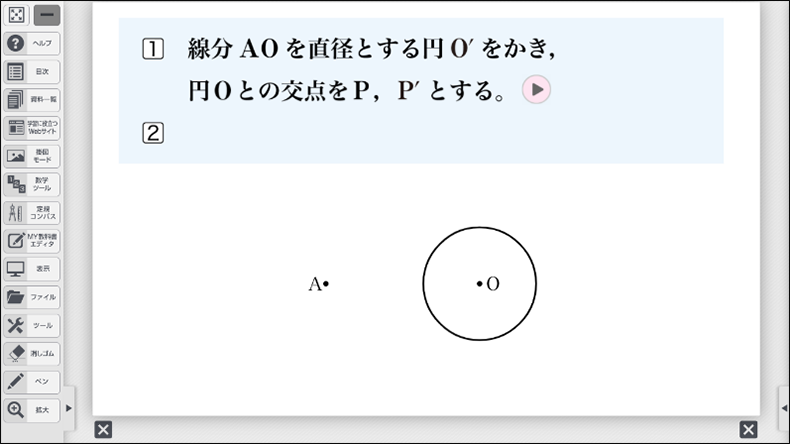
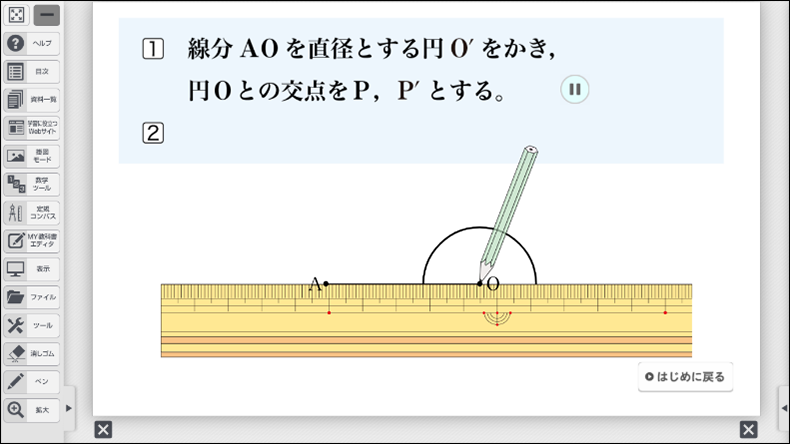
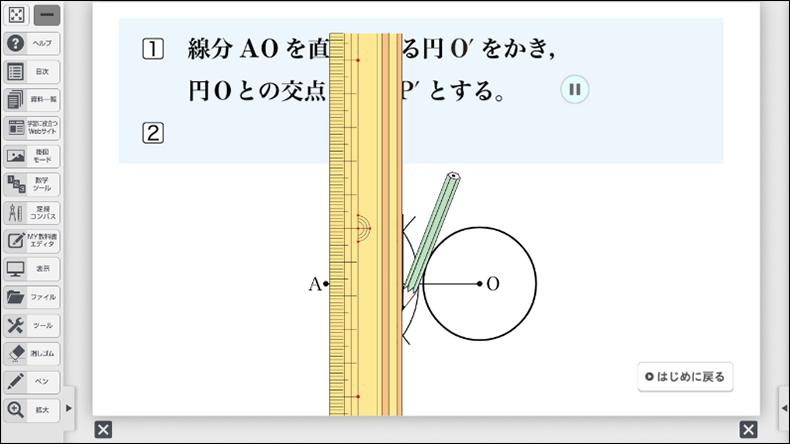
大切なのはこの後の課題で、「なぜ、この作図方法でかくと、\(\text{AP}\) と \(\text{AP´}\) が接線になるのか」を理解できるかどうかです。作図方法の理由を考えるにあたって、「直径と円周角の定理」をもとにすることで、知識の活用を学ぶことができるのです。
作図方法を説明するには、点 \(\text{O}\) から点 \(\text{P}\) と \(\text{P´}\) へそれぞれ直線を伸ばし、その結果できる \(\angle\text{OPA}\) と \(\angle\text{OP´A}\) を考える必要があります。\(\text{AO}\) を直径とすれば、直径と円周角の定理によって、2つの角とも90°になることがわかります。よって、\(\text{OP} \perp \text{AP}\)、\(\text{OP´} \perp \text{AP´}\) となり、中学1年で学習したように接線と半径を示す線分は垂直になることから、\(\text{AP}\) と \(\text{AP´}\) は円 \(\text{O}\) の接線であることが説明できます。
以上の課題を行う際、作図方法をしっかりと確認しておくことが重要です。なお、デジタルコンテンツでは、作図方法をアニメーションで確認することができます。作図方法がわからない生徒には、アニメーションを先に提示し、段階ごとに「今、何の作図をしているか」「何のためにその作図をしているのか」を確認させながら、スモールステップで学習する方法も考えられるでしょう。デジタルコンテンツのよさは、必要に応じて戻ったり、途中で止めたり、何度も確認したりすることができることです。活用することをぜひおすすめします。
②まとめ
今回の作図方法は、前回の実践で紹介した「海上にいる船の位置を作図で求める課題」にもつながります。課題解決をするうえで必要な過程なので、ここでしっかりと作図方法を確認しておくことが大切です。デジタルコンテンツを利用することで、個々の技能や学力差にうまく対応しながら進めていくとよいでしょう。
その他のコンテンツ