今日の授業のひと工夫（小中学校）

6年p.39～40（前時）で乗数を分数に拡張し、p.41では計算の仕方を考えます。
p.41では、かけ算の性質（乗数が \(n\) 倍になれば、積も \(n\) 倍になる）を用いたこうたさんの考えと、ペンキの量という具体場面に基づいて段階的に説明したしほさんの考えを掲載しています。

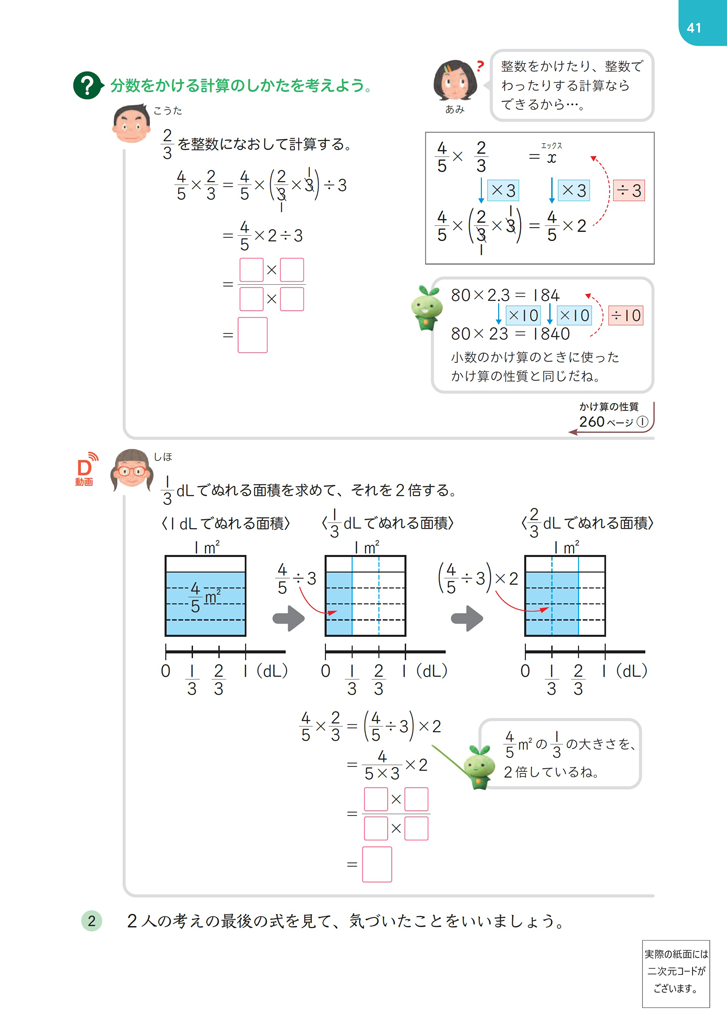
かけ算の性質は、4年、5年の小数のかけ算などでも重視して掲載していますが、児童の定着がよいとはいえません。ここでも、しほさんの考えのほうに納得感が強い児童が多いかもしれませんが、かけ算の性質も再度押さえておきたいところです。
少し先を見据えると、中学生になって、\(\dfrac{b}{a}\div \dfrac{d}{c}=\dfrac{b}{a}\times \dfrac{c}{d}\) が成り立つ理由を正しく答えられる生徒は（大人も含めてですが）、残念ながら多くありません。もちろん、p.51のような具体場面を用意して、p.54のように説明もできるのですが、わり算の性質（被除数と除数を \(n\) 倍しても、商は変わらない）で説明するほうが簡潔です。

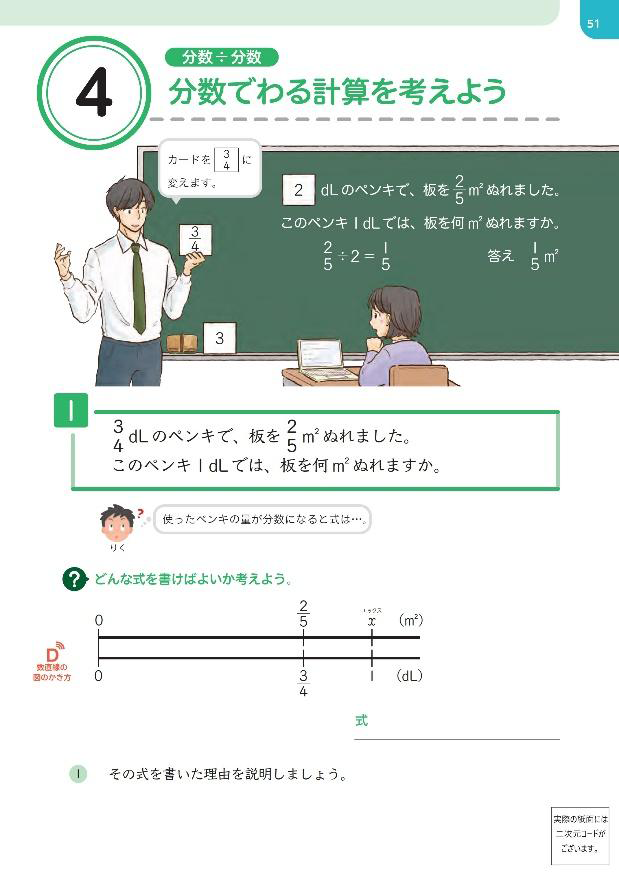
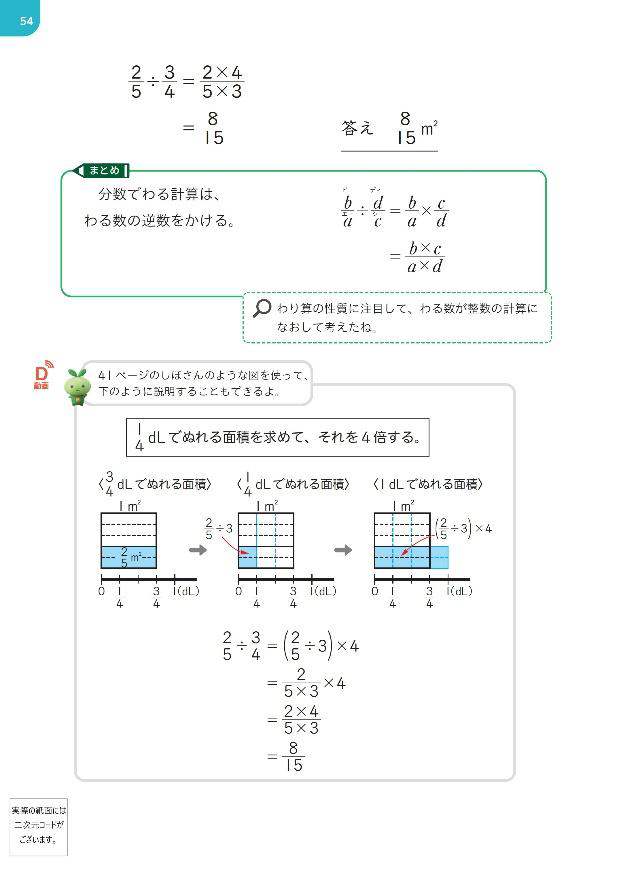
▲新しい算数6 p.51、54

単に知識・技能として分数のかけ算やわり算の計算ができるだけではなく、その計算の仕組みを理解することも大切です。分数のかけ算でかけ算の性質を大切に扱うことで、分数のわり算でわり算の性質を用いることが自然になります。このように、学習がつながっていくと、児童の理解も深まっていきますね。