今日の授業のひと工夫（小中学校）

6年p.33では、分数\(\times\)整数の立式をし、計算の仕方を考えていきます。 ここでは、\(\dfrac{3}{7}\times 2\) を扱うため、小数\(\times\)整数、分数\(\times\)整数の計算の仕方を考えるときに、単位小数や単位分数の「(\(3\times 2\))こ分」という共通性に着目できるように、\(0.3\times 2=0.6\) の式を導入で取り上げています。

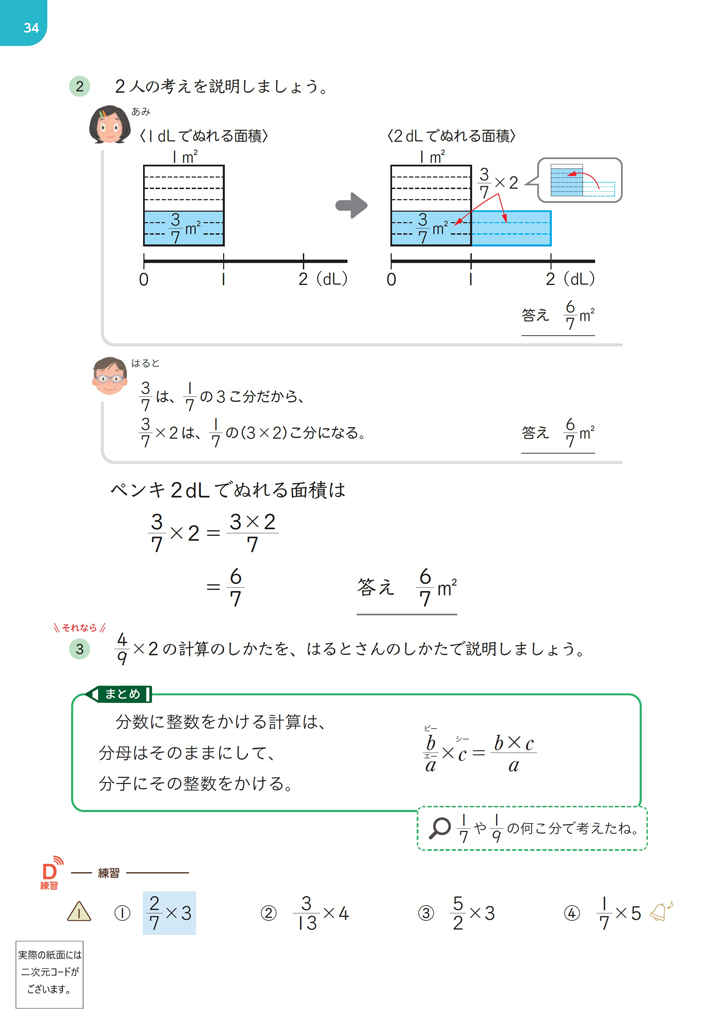
▲新しい算数6 p.33、34

まず、1dLで0.3m²ぬれるペンキがあるとき、2dLでぬれる面積を求める \(0.3\times 2=0.6\) を提示します。そして、1dLでぬれる面積が分数\(\left(\dfrac{3}{7}\right)\)になったらどうなるかを考えさせます。数直線の図を活用するなどして \(\dfrac{3}{7}\times 2\) を立式したのち、計算の仕方を考えていくわけですが、ここで小数\(\times\)整数において、単位小数0.1の何こ分かに着目したことを想起させ、単位分数である\(\dfrac{1}{7}\) の何こ分かに着目させることが大切です。

\(0.3\times 2\) の計算の仕方を考えるときは、単位小数の0.1に着目して、「0.1の(\(3\times 2\))こ分」であると考えました。これを踏まえて、\(\dfrac{3}{7}\times 2\) の計算の仕方を考えると、同じように単位分数に着目して、「\(\dfrac{1}{7}\) の(\(3\times 2\))こ分」であると考えることができます。
解決の見通しをもつ段階や自力解決の段階で、単位分数の何こ分かに着目している児童（p.34はるとの考え）がいたら、学級全体で共有し価値づけることも大切です。
まとめでは、分数\(\times\)整数の計算について、「単位分数の何こ分かに着目し、整数の乗法計算に帰着させて考える」という数学的な見方・考え方を価値づけましょう。