今日の授業のひと工夫（小中学校）

「新しい数学」3年7章p.206章の問題A \(\boxed{\ 6\ }\) は、直角三角形の各辺を1辺とする正方形を正三角形に変えても、\(P+Q=R\) の関係が成り立つことに気づかせる問題です。

この問題から、さらにどんな図形であればこの関係が成り立つのかを考えさせるとよいでしょう。すなわち、直角三角形の各辺をそれぞれ対応する辺にもつ相似な図形をつくれば、それらの面積の間に \(P+Q=R\) の関係が成り立つことに気づかせたいところです。
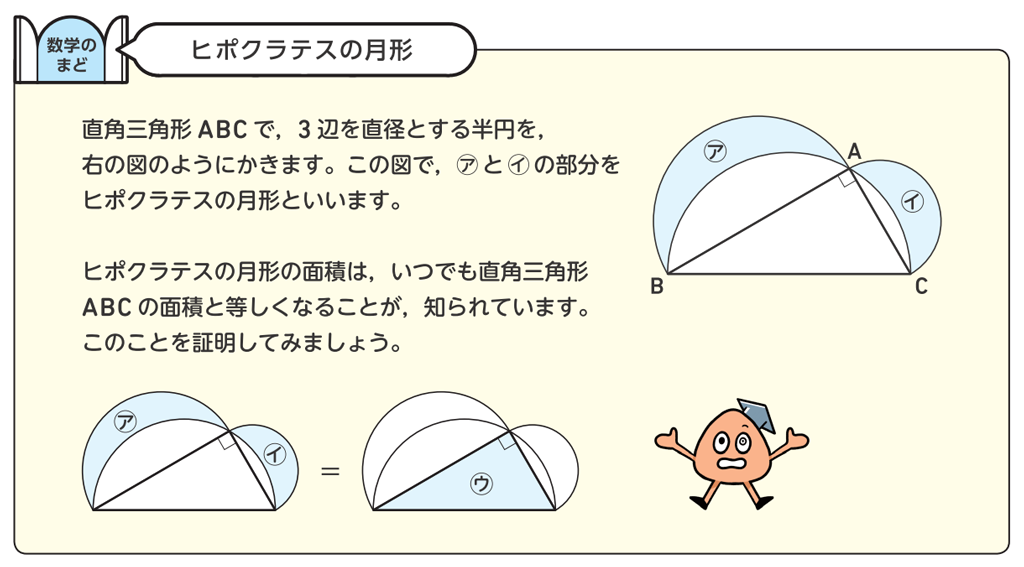
このことは、面積比が相似比の2乗になることからも納得できるでしょう。例えば、正五角形や半円など、いつでも相似な図形のほか、一般の相似な図形であれば、どんな図形であってもよいことがわかります。直角三角形の各辺を直径とした半円をつくって、斜辺の半円をひっくり返した図を、p.205数学のまど「ヒポクラテスの月形」で紹介しています。関連して取り上げて、直角三角形の理解をさらに深めたいですね。