今日の授業のひと工夫（小中学校）

1年4章p.120、121では、小学校で学んだ比例と反比例を見なおします。見開きページでそれぞれの特徴を対比することができます。

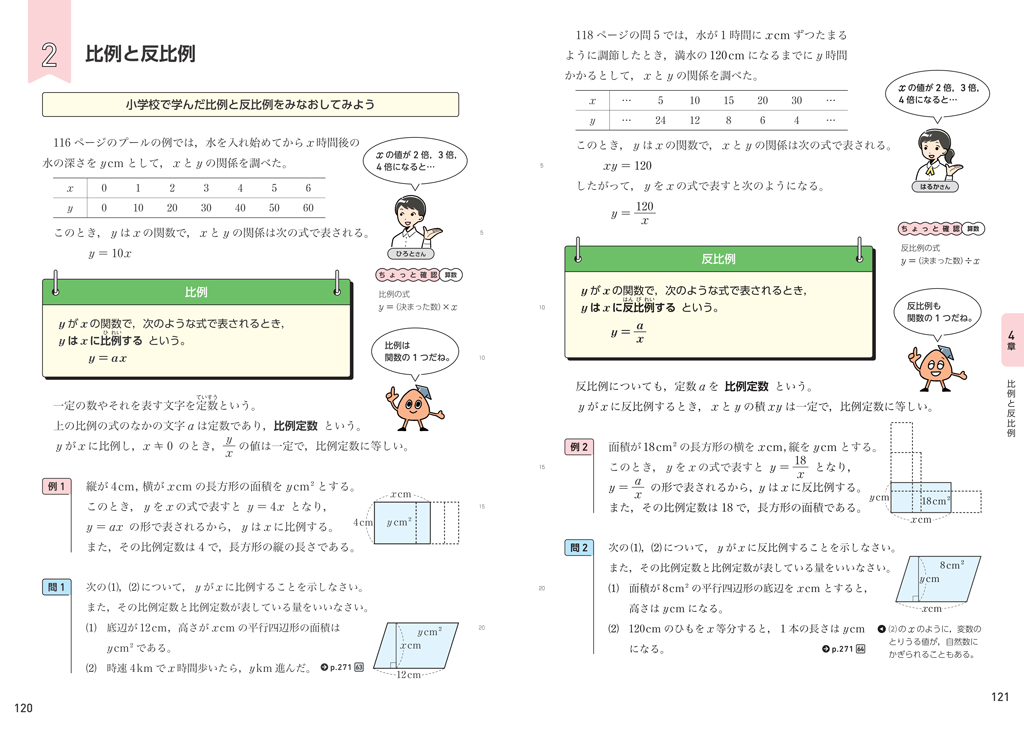
小学校では、2つの量□と○があり、□が2倍、3倍、…になると、それにともなって○が\(\dfrac{1}{2}\)倍、\(\dfrac{1}{3}\)倍、…になるとき、○は□に反比例すると定義しました。中学校では、比例\(y=ax\)と同様に、反比例を式\(y=\dfrac{a}{x}\)で定義します。

また、反比例の場合、見方を変えると、「\(y\)は\(\dfrac{1}{x}\)に比例する」つまり、「\(y\)は\(x\)の逆数に比例する」と捉えることができます。このような見方で比例と反比例を関連づけることによって、それぞれの理解を深めたいですね。こうした見方をしておくと、2年で学習する1次関数\(y=ax+b\)は、\(y-b=ax\)とみれば、「\(y-b\)は\(x\)に比例する」、3年で学習する関数\(y=ax^2\)は、「\(y\)は\(x^2\)に比例する」と捉えることにつながり、関数の理解がますます深まりますね。

一方で、比例\(y=ax\)の場合は「\(y\)は\(x\)に比例する」ので、比例定数は\(a\)となり、反比例\(y=\dfrac{a}{x}\)の場合は「\(y\)は\(\dfrac{1}{x}\)に比例する」ので、このときの比例定数が\(a\)となりますね。

また、比例と反比例の積や商の値に着目してみると、比例の場合、\(x\)と\(y\)の商\(\dfrac{y}{x}\)の値が一定であり、反比例の場合、\(x\)と\(y\)の積 \(xy\) が一定であることがわかります。

▲新しい数学1 p.120、121

例1と例2、問1と問2ではそれぞれ同じ題材を扱っています。\(xy\)の値が一定、\(\dfrac{y}{x}\)が一定という比例と反比例の見方と関連づけながら、簡単に触れておくとよいでしょう。

比例と反比例を様々な見方で捉えることはとても重要です。全国学力・学習状況調査の結果でも、定着が良くないことが指摘されています。それぞれの理解を深めることを大切にしたいですね。

関連記事はこちら
＞【1年4章】小学校で学んだ比例と反比例を見直してみよう