今日の授業のひと工夫（小中学校）

「新編 新しい数学」3年巻末p.264「瞬間の速さ」では、p.112のジェットコースターの平均の速さをもとに瞬間の速さについて考えます。

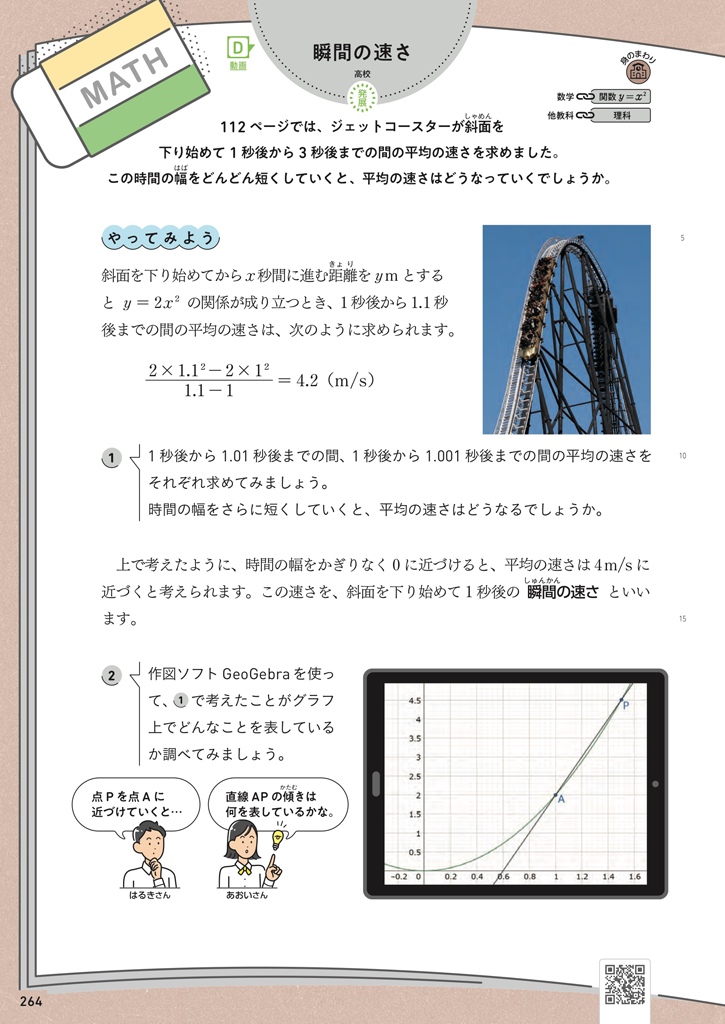
関数 \(y=f(x)\) において、\(x\) の値が \(a\) から \(b\) まで変化するとき、\(x\) の変化量 \(b-a\) と、\(y\) の変化量 \(f(b)-f(a)\)との比の値

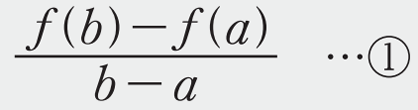
を、\(x\) の値が \(a\) から \(b\) まで変化するときの関数 \(y=f(x)\) の平均変化率といいます。また、\(b\) を \(a+h\) でおきかえると、平均変化率は

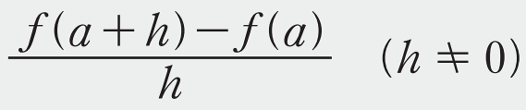
と表されます。ジェットコースターが \(x\) 秒間に進む距離を \(y\) mとし、\(y=2x^2\) の関係が成り立つとき、この関数を \(y=f(x)\) とすると、1秒後から \((1+h)\) 秒後までの平均の速さは

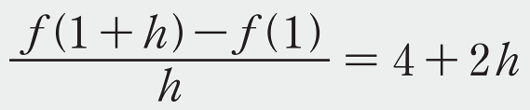
となります。\(h\) を限りなく0に近づけると、\(4+2h\)はかぎりなく4に近づきますね。この値は、1秒後の瞬間の速さを表していると考えられます。

①で、時間の幅を短くして考えた平均の速さから瞬間の速さを考えていくことが、この \(h\) をかぎりなく0に近づけていることになりますね。

②では、この考え方が、グラフ上で表していることを考えます。はるきさんやあおいさんの吹き出しをきっかけにして、

• 時間の幅をかぎりなく０に近づけるということは、点\(\text{P}\)を点\(\text{A}\)に近づけるということ
• 直線\(\text{AP}\)は放物線の接線に近づいていくということ
• 点\(\text{P}\)と点\(\text{A}\)が一致するとき、直線\(\text{AP}\)は放物線の接線となり、その傾きは瞬間の速さを表していること

などに気づくことを期待したいですね。

高校で学習する内容ですが、平均の速さの学習の際に扱ってみてもよいかもしれませんね。