今日の授業のひと工夫(小中学校)
- TOP
- 今日の授業のひと工夫(小中学校)
- 【3年7章】長方形の辺の長さの比とピタゴラス数

「新編 新しい数学」3年7章p.206問1では、\(\triangle \text{ABF}\)や\(\triangle \text{EDF}\)に着目すると、長方形の辺の長さの比とピタゴラス数との関係を見つけることができます。
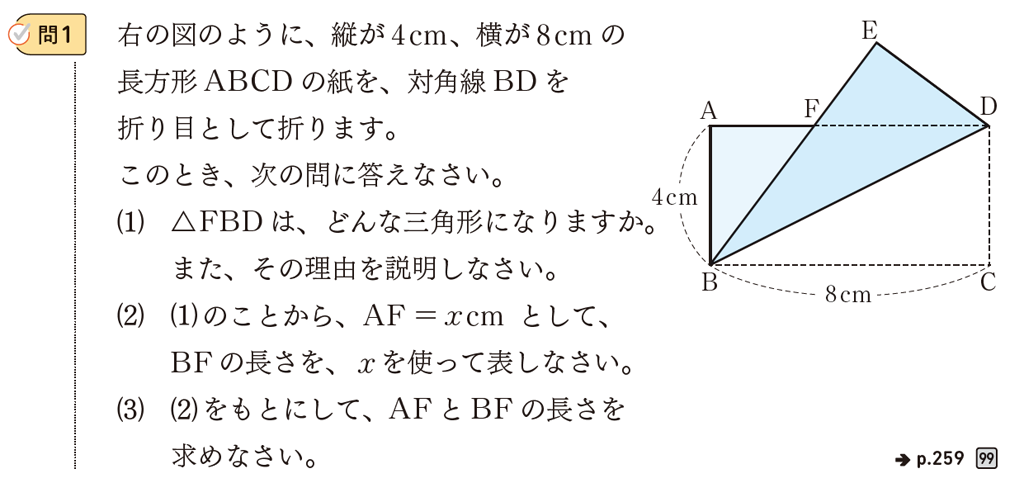
問1では、長方形ABCDの辺の縦と横の長さの比が\(1:2\)になっていますね。このとき、\(\triangle \text{ABF}\)は辺の長さが、\(\text{AF}=3\)cm、\(\text{AB}=4\)cm、\(\text{BF}=5\)cmとなり、\(3:4:5\)の直角三角形になっています。
それでは、長方形の縦と横の長さの比が\(2:3\)のとき\(\triangle \text{ABF}\)はどんな三角形でしょうか。\(\text{AB}=12\)cm、\(\text{AD}=18\)cmとして計算すると、\(\text{AF}=5\)cm、\(\text{BF}=13\)cmとなり、\(\triangle \text{ABF}\)は\(5:12:13\)の直角三角形になります。さらに、縦と横の長さの比が\(1:4\)のときは、\(8:15:17\)の直角三角形になります。
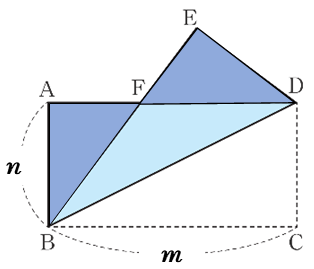
この長方形の縦と横の長さの比が自然数の比であれば、\(\triangle \text{ABF}\)は3辺の比に必ずピタゴラス数が現れるのでしょうか。
\(\text{AB}=n\) 、\(\text{AD}=m\)、\(\text{AF}=x\)として考えてみましょう。
\(\begin{aligned} \text{AB}^2+\text{AF}^2 & =\text{BF}^2 \\
n^2+x^2 & ={(m-x)}^2 \\
x & =\cfrac{m^2-n^2}{2m}\end{aligned}\)
\(\triangle \text{ABF}\)の弧は
\(\text{AF}=\dfrac{m^{2}-n^{2}}{2m}\) 、\(\text{AB}=n\) 、\(\text{BF}=\dfrac{m^{2}+n^{2}}{2m}\)
となります。
\(\text{AF}\)、\(\text{AB}\)、\(\text{BF}\)にそれぞれ \(2m\) をかけると
\(m^{2}-n^{2}\)、\(2mn\)、\(m^{2}+n^{2}\)
となり、ピタゴラス数を見つけるための式が出てくることがわかります。この式は、【3年7章】ピタゴラス数を見つけてみようの記事でも紹介しています。
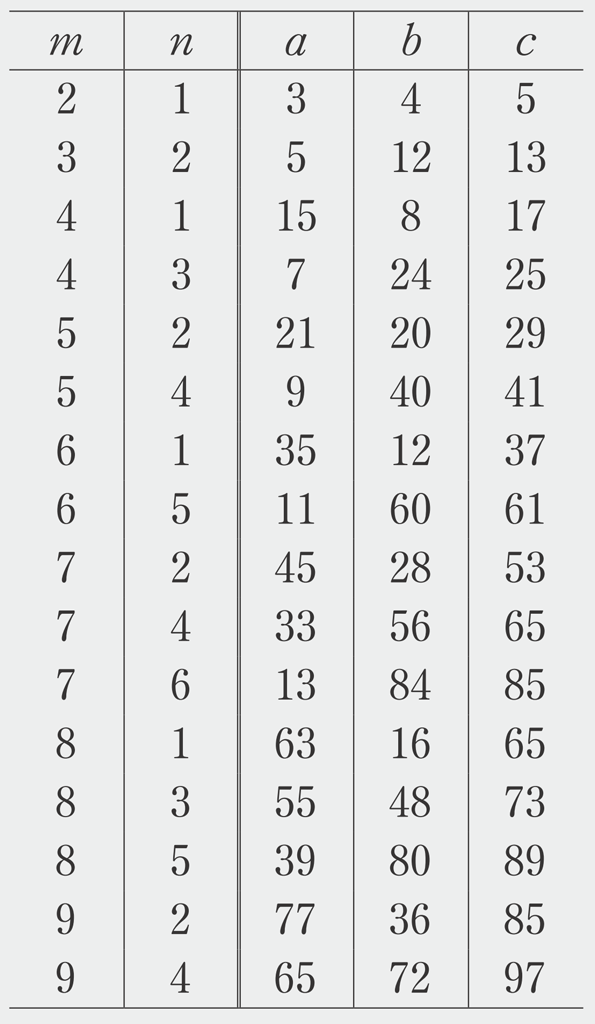
このように考えると、問1で3、4、5の直角三角形が出てきたのは、偶然ではなかったことがわかりますね。直角三角形の比に着目した生徒がいたら、授業で取り上げてみてください。
関連記事はこちら
その他のコンテンツ
