今日の授業のひと工夫(小中学校)
- TOP
- 今日の授業のひと工夫(小中学校)
- 【3年6章】星形の角の和

「新編 新しい数学」3年6章「数学のまど」では、星形の角の和について考えます。星形五角形の先端にできる角の和は、2年p.124の章の問題で扱っています。そこでは、多角形の角の性質や、平行線の性質などを利用して角の和を求めました。
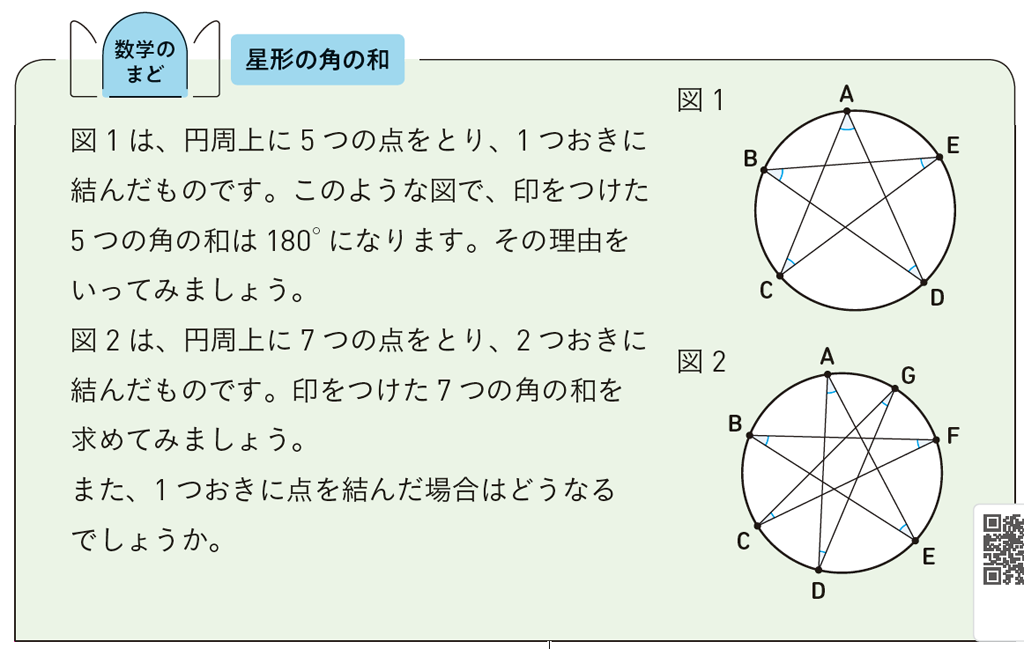
3年では、星形の頂点が円周上にある場合を考え、円周角の定理を用いても求められることに気づかせたいところです。2年生のときに、この星形五角形の問題を扱っていない場合や定着が弱かった場合は、レポート課題や小テスト等で2年の問題を事前に考えさせておくとよいでしょう。
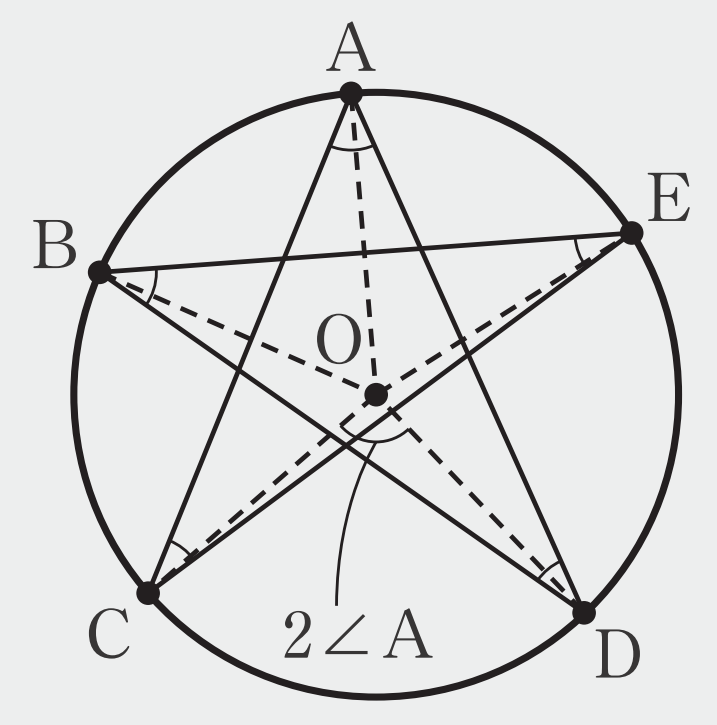
図1の場合、右の図のように、中心角におきかえて考えることができます。このとき、\(2\text{(}\angle \text{A}+\angle \text{B}+\angle \text{C}+\angle \text{D}+\angle \text{E)}=360^\circ\) となり、先端の角の和は \(180^\circ\)と導くことができます。このことから、「円周全体に対する円周角(の和)は\(180^\circ\)である」と考えることもできますね。図2も同様に考えることができます。
また、円周上に7つの点をとり、1つおきに点を結んだ場合は、それぞれの円周角に対する弧がちょうど円周3周分になるため、先端にできる角の和は\(540^\circ\)であることがわかります。星形多角形の先端にできる角の和の規則性に興味をもつ生徒もいるでしょう。生徒の実態に応じて課題を出せるようにしておきたいですね。
この星形多角形の先端にできる角の和を一般化して考えると次のようになります。
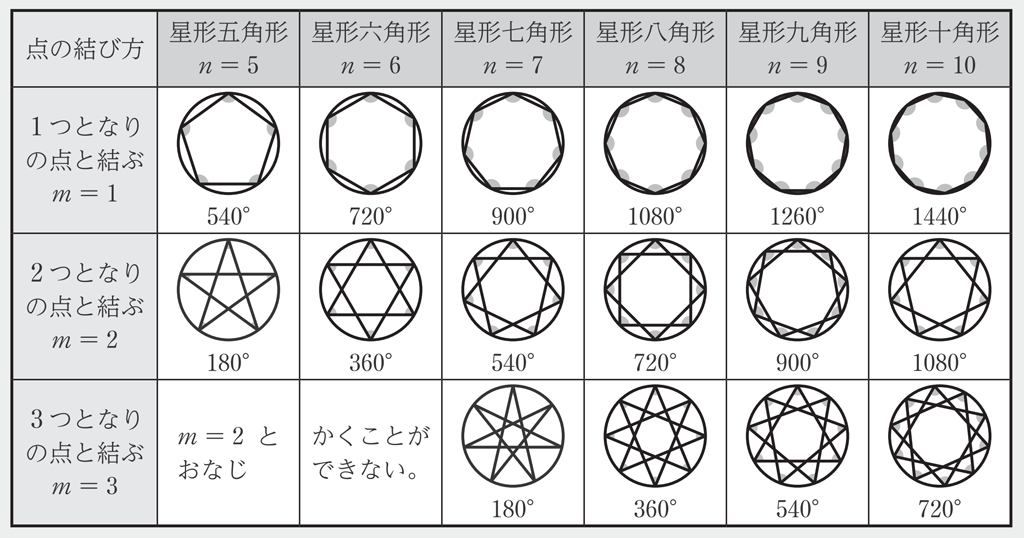
円周上に \(n\) 個の点をとり、ある点からはじめて円周上の \(m\) 個となりの点を同じ回り方で次々に結んで星形多角形をつくります(\(n=6\) 、\(m=2\) の星形多角形のように、はじめの頂点に戻ったときに他の頂点が残っている場合は、残った頂点から同じように続けます)。このとき、先端にできる角の和は、次の表のようになり、角の大きさを表す式は \(180^\circ \times (n-2m)\) となります。このような簡潔な式に表せることは、生徒の興味・関心をひくことでしょう。また、この式は様々な方法で導出することができるので、このことをレポート課題にしてもおもしろいかもしれませんね。
その他のコンテンツ
