今日の授業のひと工夫(小中学校)
- TOP
- 今日の授業のひと工夫(小中学校)
- 【1年4章】小学校で学んだ比例と反比例を見直してみ…

「新編 新しい数学」1年4章p.124では、p.120の水そうの例を振り返り、比例の意味を理解し、比例の関係を式に表せるようにすることをねらいとしています。p.125の反比例でも、同じように前の項で扱った例を振り返り、反比例の意味を理解し、反比例の関係を式に表せるようにしたいところです。
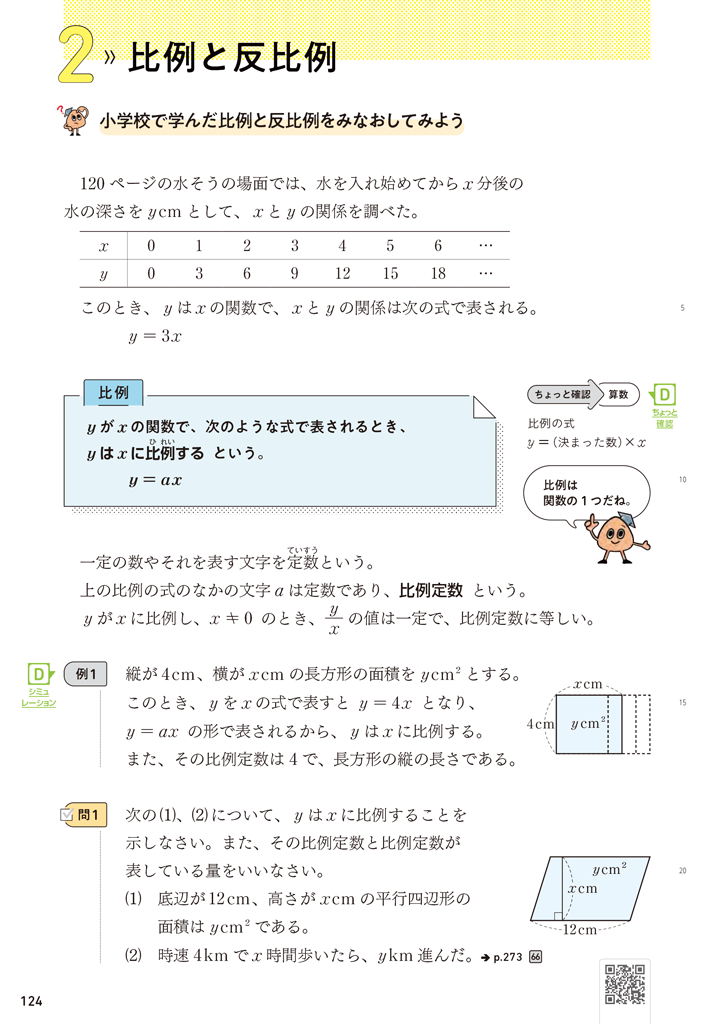
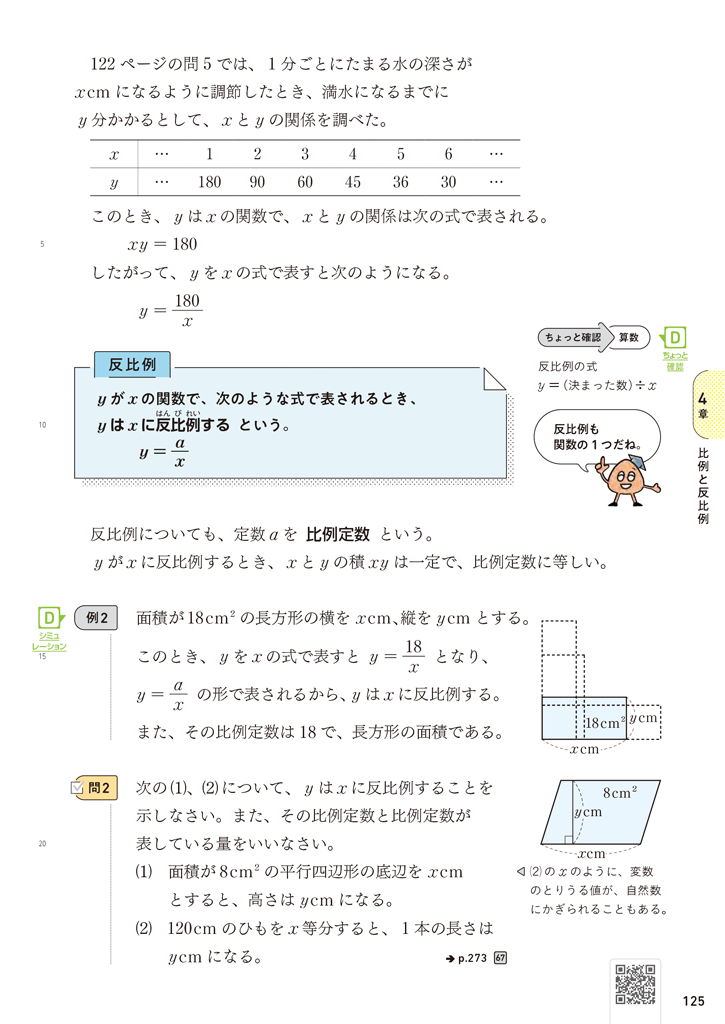
▲1年 p.124、125
教科書では、「比例」と「反比例」を同時に定義しています。これには、前項「関数」に続く形で比例と反比例を定義することによって、小学校で学習した比例と反比例を、関数という目で見直すことを強調する意図があります。
小学校では、2つの量□と○があり、□が2倍、3倍、…になると、それにともなって○も2倍、3倍、…になるとき、○は□に比例すると定義しました。中学校では、比例を関数として捉えなおし、\(y=ax\) という式で定義します。「\(x\) の値を決めれば、\(y\) の値がただ1つに決まる」ことが判断しやくなる式に表すことのよさを、小学校の定義との違いと合わせて、確認したいところですね。


比例と反比例のまとめでは、比例定数や \(x\) と \(y\) の商、積が一定であることなど、比例と反比例の定義に関連することがらについて、共通する点や異なる点を比較することによって、それぞれの理解を深められるようにしたいところです。これからの学習の土台となる知識であるため、ていねいに指導するよう心がけたいですね。
その他のコンテンツ
