今日の授業のひと工夫（小中学校）

「新編 新しい数学」2年3章p.88では、図形の辺上を動く点によってできる図形の面積の変化を、1次関数の式やグラフで表していきます。

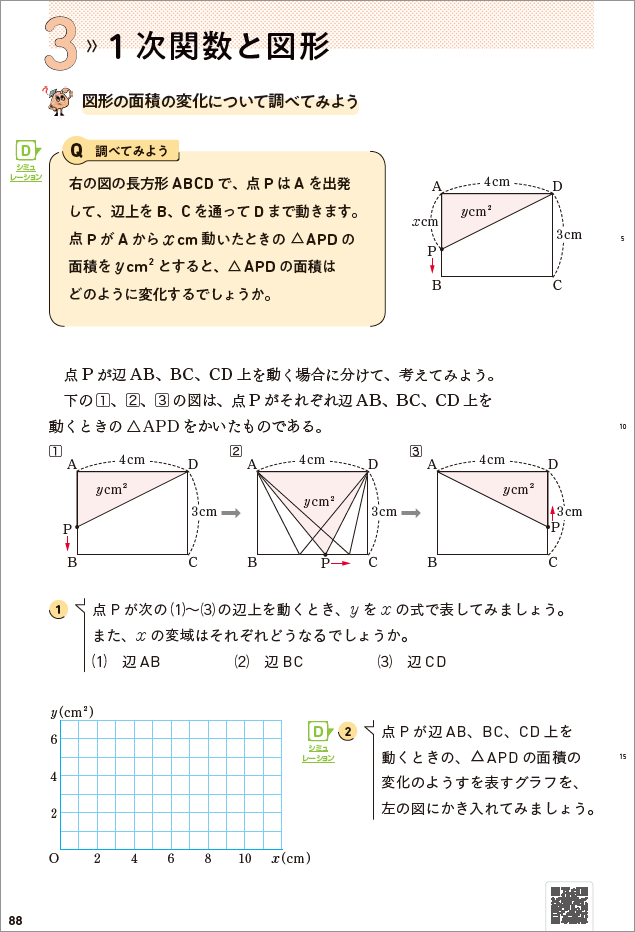
Qでは、あたえられた変数 \(x\) の意味を正しく理解し、△APDの面積 \(y\) を \(x\) の関数として表していきます。その際に、\(x\) の変域により関数が異なることに生徒自身が気づくようにしたいところですね。

①(2)の式は \(y=6\) となります。\(y=k\) のグラフの意味はp.79で学習していますが、そこでは2元1次方程式のグラフの特別な場合として学習しました。

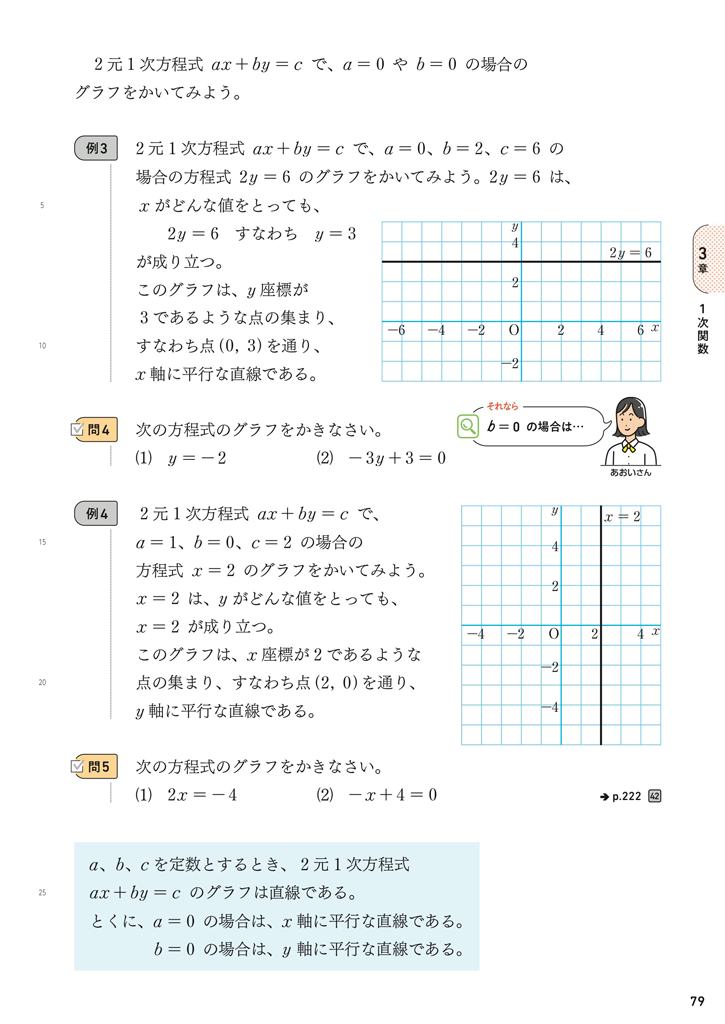
\(x\) の値に関わらず、つねに一定の値をとる定数関数としての扱いはこのp.88が初めてとなります。定数関数について、このような具体的な場面の考察を通して、理解を深めることが期待できますね。

ここでは、QRコンテンツを使用したり、図を示したりすることで、\(x\) の値に関わらず面積はつねに6cm\(^2\)であることが理解できるでしょう。そして、面積がつねに6cm\(^2\)であることは、\(x\) の値に関わらないので、式で表すと \(y=6\) となることを確認したいところですね。

(3)において、\(x\) の変域や式がわからない生徒には、次のような図をかいて、PD \(=10-x\) であることをおさえることも考えられます。

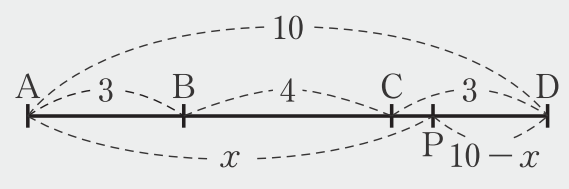
この図から、\(x\) の変域が \(7 \leqq x \leqq 10 \) であることがわかります。また、△APDが底辺4cm、高さ\((10-x)\)cmの三角形であることから、次のような式になることが理解しやすくなりますね。

\(y= \frac{1}{2} \times 4 \times (10 – x)\)
\(=-2x+20\)  

また、問題場面から式をつくることが難しい生徒には、先にグラフをかかせる活動を行い、グラフから2点(7,6)、(10,0)を通る直線の式を求めてみるよう伝えてもよいですね。

関連記事はこちら

＞【2年3章】図形の面積の変化について調べてみよう

QRコンテンツはこちら

＞\(\triangle\)APDが変わるようすを見てみよう

• 本サイト内の二次元コードまたはURLのリンク先に掲載されているコンテンツは、教材研究の範囲内で利用することができます。当該の検定教科書を採択または購入して使用していない場合、授業や自宅等での個人学習に利用することはできません。
• また、当該のコンテンツが掲載されているURLから遷移して、他のコンテンツを利用することはご遠慮ください。