
前回,ニュートンの冷却の法則を使って,方程式(漸化式)を立てれば,未来の温度も計測していない過去の温度も推測できることをみました。このことを使って,死亡推定時刻について考えます。死亡推定などと日常的には使わないややショッキングな用語を持ち出しましたが,推理小説の材料ですからご容赦を。
その前に,温度を方程式で扱う際の一般的な注意をしておきましょう。
【絶対温度とセルシウス温度】
例えば,今年の夏は去年の夏の2倍暑いとはいいませんね。気分的にはそうだとしても。\(40\text{℃}\) は \(20\text{℃}\) の2倍であるともいいません。その理由は温度の原点が \(0\text{℃}\) でないからです。原点をもつ温度は,絶対温度(熱力学温度)で,単位はケルビン(\(\text{K}\))です。絶対温度を \(T\) としたとき,ほぼ氷点である参照温度 \(T_{ref} =273.15\text{K}\) との差をセルシウス温度(Celsius temperature)といい,それを例えば \(\theta\) と書いて
\(\theta=T-T_{ref}\)
と定義します。セルシウス温度の単位はセルシウス度(degree Celsius)で記号は \(\text{℃}\) です。セルシウス度で表したセルシウス温度の数値はケルビンで表した絶対温度の数値に対して次の関係を持ちます。
\(\cfrac{\theta}{\text{℃}}=\cfrac{T}{\text{K}}-273.15\)
目盛間隔の \(1\text{℃}\) と \(1\text{K}\) は等しいです。
【例1】 \(\theta=30\text{℃}\) は \(T= 303.15\text{K}\) です。これは,次の関係に他なりません。
\(\cfrac{\theta}{\text{℃}}=30=303.15-273.15=\cfrac{T}{\text{K}}-273.15\)
【例2】 2つの温度
\(\theta_1=20\text{℃}\) ⇔ \(T_1=293.15\text{K}\)
\(\theta_2=40\text{℃}\) ⇔ \(T_2=313.15\text{K}\)
が与えられたとき,これらの温度差は次のようになります。
\(\theta_2-\theta_1=20\text{℃}\),\(T_2-T_1=20\text{K}\)
このように,セルシウス温度と絶対温度のどちらを用いても温度差や温度間隔は等しいです。しかし,絶対温度の比 \(\cfrac{T_2}{T_1}\) は計算できますが,セルシウス温度の比の計算はできません。この例では,\(\theta_2\) は \(\theta_1\) に比べて,温度差でいうと \(20\text{℃}\) 高く,温度比でいうと \(\cfrac{T_2}{T_1}\fallingdotseq1.1\) 倍程度高い,ということになります。
一般に,方程式の未知関数や未知変数に用いられる温度は絶対温度です。しかし,方程式に温度差しか出てこない場合,温度の単位がケルビンでもセルシウス度でも数値は同じです。前回,ニュートンの冷却の法則についてセルシウス温度を用いて表した理由(そして,本来は絶対温度を使うべきだから,記号 \(T\) を使った理由)はここにあります。
\(\theta\) はカタカナだとシータ,テータと書きます。ラテン文字の th に対応します。t のような発音なので,温度(temperature)に対応する文字として \(T\) と共に使われます。一方,時間(time)に対応する文字として,\(t\) や \(τ\)(タウ)が使われます。混乱しなければ,\(t\) を温度に,\(T\) を時間に使うこともあります。
【死亡推定時刻】
死体の発見時には以下の状況でした。
23:30 鑑識官到着。死体の温度 \(\ 29.3 \text{℃}\)
24:30 1時間後の死体の温度\(\ 28.8 \text{℃}\)
特記事項 室温は一定に保たれていて,\(21.0 \text{℃}\) であった。
【疑問】死亡時刻を推定できるか。
【答】前回の(3)式(の一つ上の式)
\(T_n-T_a=\text{(}1-kτ\text{)}^n\text{(}T_0-T_a\text{)}\),\(n=1,2,3,\ \) … …(1)
を使います。この式を新たに(1)式としましょう。
各記号は以下を表していました。
\(T_a\):室温
\(T_n\):\(t_n=nτ\) 時間後の温度
\(k\):物体(死体)によって定まるパラメータ
\(τ\):ある時間幅(\(0\lt kτ \lt 1\) を満たすように小さくとる)
さしあたってはっきりとわかっているのは,\(T_a=21.0\text{℃}\) と,ある時刻 \(t_n\) において \(T_n=29.3\text{℃}\) だったとすると,その1時間後の時刻「\(t_n+1\) 時間後」において \(28.8 \text{℃}\) であることだけです。\(T_n-T_a\) や \(T_0-T_a\) という温度差だけを問題としているので,セルシウス温度で温度を表現しても問題ありません。
さて,初期温度 \(T_0\) もパラメータ \(n\),\(τ\),\(k\) も不明です。また,「\(t_n+1\) 時間後」が綺麗に \(t_m=mτ\) のように書けるかもわかりません。このままでは死亡時刻を求めるのは難しそうなので,以下のようにアプローチしてみます。わかりやすいように,アプローチの段階を3段階にわけます。
【第1段】
まず,離散的な時間を連続的にすることを考えます。そのために次の変形をおこないます。\(n=\cfrac{t_n}{τ}\) から,
\(\text{(}1-kτ\text{)}^n=\text{(}1-kτ\text{)}^\frac{t_n}{τ}=\Large{(}\) \(\text{(}1-kτ\text{)}^\frac{1}{τ} \Large{)}\) \(^{t_n}\)
これより,\(R=\text{(}1-kτ\text{)}^\frac{1}{τ}\) とおくと,\(\text{(}1-kτ\text{)}^n=R^{t_n}\) となるので,(1)式に代入して,
\(T_n-T_a=R^{t_n}\text{(}T_0-T_a\text{)}\),\(n=1,2,3,\) … …(2)
を得ます。\(t_n\) は飛び飛びの離散的な時間を表していて,\(T_n\) はその離散時間における値(温度)です。そこで,エイヤッと,(2)式において離散時間 \(t_n\) を連続時間 \(t\) に変えて,それに応じて離散値 \(T_n\) を連続関数 \(T\text{(}t\text{)}\) に置き換えます。
\(T\text{(}t\text{)}-T_a=R^t\text{(}T_0-T_a\text{)}\),\(t \geqq 0\) …(3)
これより,\(R^0=1\) とすると,\(T\text{(}0\text{)}=T_0\) となります。また,\(t=t_n\) のとき,\(T\text{(}t_n\text{)}=T_n\) と定めれば,(3)式は(2)式を含みます。よって,(3)式は離散時刻 \(t_n\) と \(t_{n+1}\) の間の時間における温度についても考えられることになります。
【第2段】
鑑識官が到着したときの死体の温度は \(29.3 \text{℃}\) でした。死亡してからの時間がわかりませんが,\(t=t_*\) とすると,
\(T\text{(}t_*\text{)}=29.3\text{℃}\)
となります。また,時間 \(t\) の単位を時(hour)として,\(t_{**}=t_*+1\) とおくと,
\(T\text{(}t_{**}\text{)}=28.8\text{℃}\)
です。これらの値を(3)式に代入します。
\(T\text{(}t_*\text{)}-T_a=R^{t_*}\text{(}T_0-T_a\text{)}\) …(4)
\(T\text{(}t_{**}\text{)}-T_a=R^{t_{**}}\text{(}T_0-T_a\text{)}\) …(5)
そして,(5)/(4)を計算すると,\(t_{**}-t_*=1\) から,
\( \cfrac{T(t_{**})-T_{a}}{T(t_{*})-T_{a}}=R^{(t_{**}-t_{*})}=R^{1}=R\) …(6)
のように \(R\) の値が求まりました。これを(3)式に代入すれば,
\( T(t)=\LARGE{ ( }\)\(\cfrac{T(t_{**})-T_{a}}{T(t_{*})-T_{a}}\LARGE{)}\large{^{t}}\)\((T_{0}-T_{a})+T_{a}\),\(t \geqq 0\) …(7)
となって,温度関数 \(T(t)\) を得ます。よって,初期温度 \(T_0\) を与えれば,\(t\) 時間後の温度 \(T(t)\) の値が定まります。
下図は,\(T_0=36.5\text{℃}\) としたときの,横軸:時間 \(t\)(hour),縦軸:温度 \(T\text{(℃)}\) の温度関数 \(T(t)\) のグラフです。12時間まで描画しました。
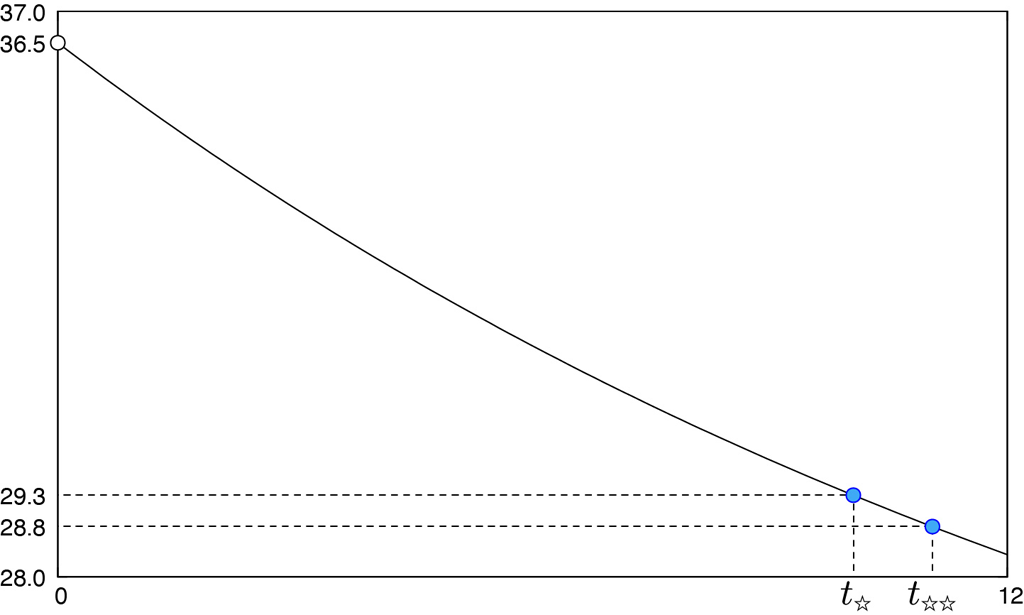
下図は,72時間まで描画した図です。ほぼ室温 \(T_a=21\) まで下がっているのがわかります。赤い四角枠の部分だけを取り出したのが上図です。
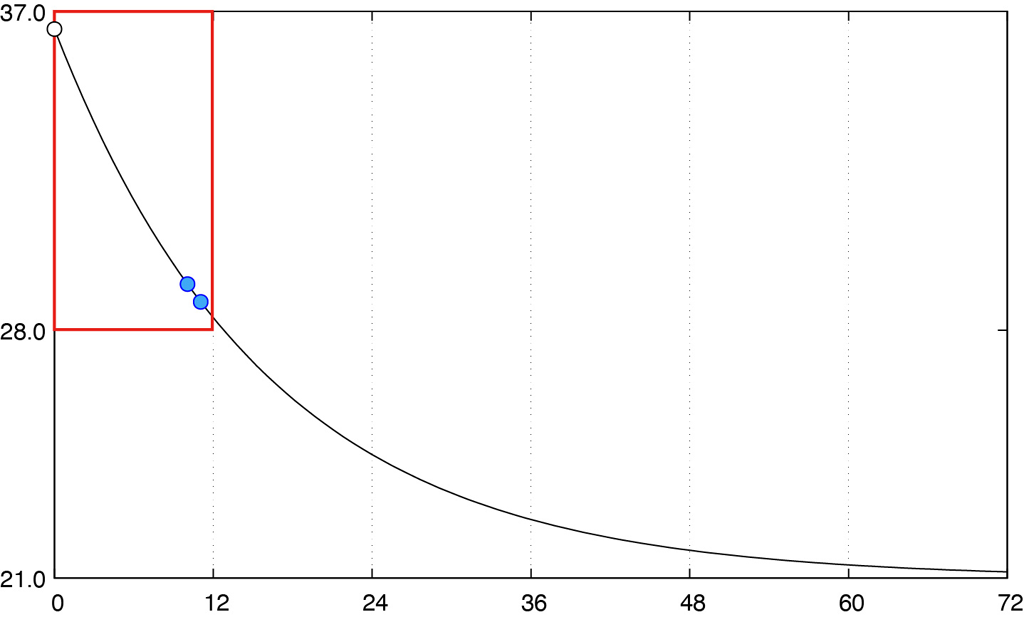
【最終段】
最後に,\(t_*\) を求めれば,鑑識官の到着時刻が \(23\text{:}30\) だから,そこから死亡推定時刻がわかります。
(4)式の両辺を \(T_0-T_a\) で割ると,
\( \cfrac{T(t_{*})-T_{a}}{T_{0}-T_{a}}=R^{t_{*}}\) …(8)
となります。ここで \(R\) の値は(6)式で定められたものです。よって,(8)式の両辺の常用対数をとると,
\( t_{*}=\cfrac{\log_{10}(\cfrac{T(t_{*})-T_{a}}{T_{0}-T_{a}})}{\log_{10}R} \)
を得ます。既知の数値を代入すると,
\( t_{*}=\cfrac{\log_{10}(\cfrac{T(t_{*})-T_{a}}{T_{0}-T_{a}})}{\log_{10}(\cfrac{T(t_{**})-T_{a}}{T(t_{*})-T_{a}})}=\cfrac{\log_{10}(\cfrac{29.3-21.0}{\frac{T_0}{\text{℃}}-21.0})}{\log_{10}(\cfrac{28.8-21.0}{29.3-21.0})} \)
となります。インターネット上でリプレックス株式会社が無料で提供している計算サイト「keisan」の「フリー計算」(※外部サイトにリンクします)を用いて計算すると,以下を得ます。死亡推定時刻は \(23\text{:}30\) から \(t_*\) を引いた時刻です。
\(\cfrac{T_0}{\text{℃}}=35.5\) のとき,\(t_*\) =8.97919107876768383851≒8時間59分
⇒ 死亡推定時刻は \(14\text{:}31\)
\(\cfrac{T_0}{\text{℃}}=36.0\) のとき,\(t_*\) =9.52483054172295547374≒9時間31分
⇒ 死亡推定時刻は \(13\text{:}59\)
\(\cfrac{T_0}{\text{℃}}=36.5\) のとき,\(t_*\) =10.05257692592074214987≒10時間03分
⇒ 死亡推定時刻は \(13\text{:}27\)
\(\cfrac{T_0}{\text{℃}}=37.0\) のとき,\(t_*\) =10.56356659576299639316≒10時間34分
⇒ 死亡推定時刻は \(12\text{:}56\)
\(\cfrac{T_0}{\text{℃}}=37.5\) のとき,\(t_*\) =11.05883098571758878829≒11時間04分
⇒ 死亡推定時刻は \(12\text{:}26\)
以上より,死亡時刻はだいたい \(13\text{:}30\) 前後,大きく範囲を見積もって \(12\text{:}00\) 〜 \(15\text{:}00\) の間と推定されます。
もし他殺だったら犯人はこの間の時間にアリバイ(前々回の冒頭参照)がない人物に絞られますね!犯人の追跡についてはまた今度。
■ ガリレオの贈り物
温度計の歴史について,はっきりとした時系列を述べることは難しそうであるが,ガリレオが初期の温度計の開発に大きく寄与したことは間違いなさそうである。ガリレオは前回「ニュートンの贈り物」で登場したガリレオ・ガリレイ(Galileo Galilei,ユリウス暦1564.2.15-グレゴリオ暦1642.1.8)である。ガリレオは名であるので,本来ならば姓のガリレイと呼ぶべきだろうが,イタリア特有の理由からファーストネームで呼ばれている。
ガリレオの残した概念やものは多い。その中にガリレオ温度計というものがある。現在も購入可能で,温度計としてではなく,インテリアとして飾られていることが多い。浮力に関するアルキメデスの原理「液体中の物体は,物体が排除した液体の重量と同じ大きさの上向きの浮力を受ける」をもとにして作られている。
※「つい考えてしまう数学」の記事一覧はこちら
1970年東京生まれ。早稲田大学理工学部数学科卒業。東京大学大学院数理科学研究科数理科学専攻博士課程修了。現在,明治大学理工学部数学科専任教授。博士(数理科学)。専門は応用数理,特に界面現象の数理解析。実験を採り入れた数学の講義で定評がある。
| 著書: | 『実験数学読本』①・②・③ (日本評論社),『次元解析入門』,『界面現象と曲線の微積分』,『動く曲線の数値計算』(以上共立出版),『大学数学の教則』(ちくま学芸文庫),『公式は覚えないといけないの?』(ちくまプリマー新書),他。 |
その他のコンテンツ
