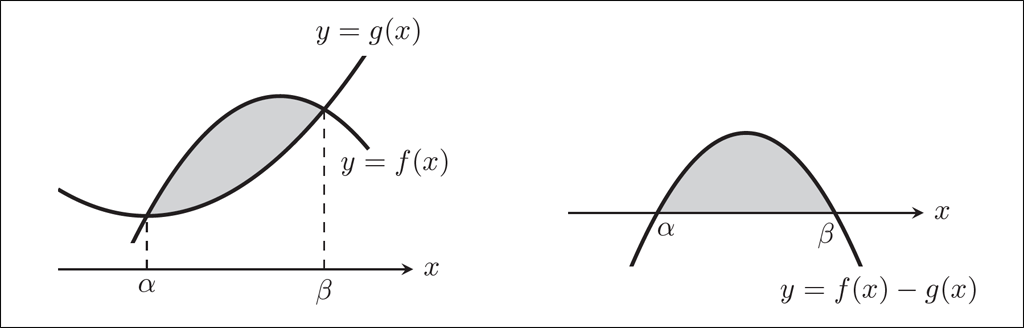特集記事（高校）

　みなさん，こんにちは。第2回の今回は，共通テスト対策にも使える話題をと思いまして，関数グラフの面積計算についてお話します。

差関数の利用

　\(y=f(x)\) と \(y=g(x)\) の2つのグラフで囲まれる部分の面積\(S\)を求めるときには「まず2つのグラフを描く！」という指導をすると思います。
　これは学習の初期段階では良いのですが，ある程度進んだら次図の灰色部分の2つの面積が等しいということを理解して活用できるようになってもらいたいものです。

　上図のどちらの灰色部分の面積にしても

\(S=\displaystyle \int_{\alpha}^{ \beta } \{f(x)-g(x)\} dx\)

という式で得られます。つまり，面積を求めるときに，\(y=f(x)\) と \(y=g(x)\)の2つのグラフを描く必要は無く，差関数 \(y=f(x)-g(x)\) のグラフだけ描けばよいということになります。\(y=f(x)-g(x)\) のグラフを描けば，共有点の \(x\) 座標は \(x\) 軸との共有点として現れるし，グラフの上下は \(f(x)-g(x)\) の符号として現れます。

　2つのグラフを描くことがそこまでメンドウでないときには，まぁ，どちらでもイイのですが，例えば「2本の3次関数のグラフによって囲まれる部分の面積」を求めるときなどには，この差関数の利用が有効です。
　というわけで，差関数を利用すると解きやすいのが次の問題です。

　文字定数を含む2本の関数グラフで囲まれる部分の面積なので，「2つのグラフを描くこと」にこだわってしまうと最初から苦労してしまいます。（解答例はこちら）

スライディング・インテグラル

　定積分の計算において，グラフの平行移動を利用するとラクに計算できる場合があります。
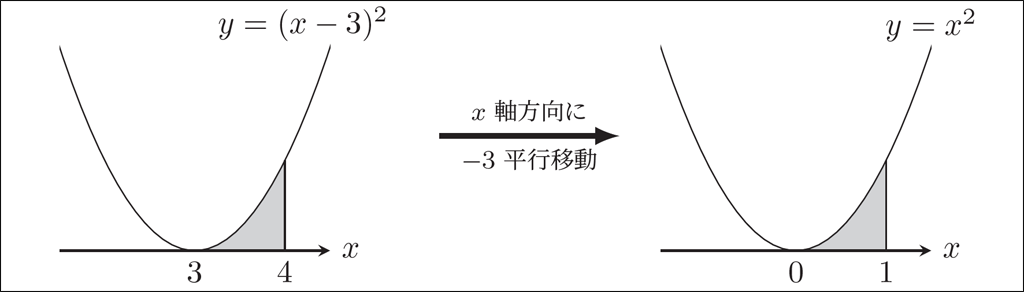
　例えば，下図（左）の灰色部分の面積は，グラフ全体を（積分区間も一緒に）\(x\) 軸方向に \(-3\) だけ平行移動した下図（右）の灰色部分の面積と等しいはずです。したがって

\(\displaystyle \int_{3}^{4 } (x-3)^2 dx = \displaystyle \int_{0}^{1 } x^2 dx = \left[ \dfrac{1}{3}x^3 \right]_0^1 = \dfrac{1}{3}\)

とできます。

　このことは，計算上は置換積分で説明できますが，図を描いて平行移動していることを説明すれば，文系の生徒にも十分理解してもらえます。
　自分はこれを「スライディング・インテグラル」とよんでいます。（笑）
　なお自分は，いわゆる「6分の1公式」もこれを利用して証明しています。

　巷では面積計算の公式がやたら細かく分類されて紹介されていたりしますが，「差関数の利用」と「スライディング・インテグラル」で（あとは力業で！）ほとんどの場合は事足ります。
　例外は「円が関係する面積」の問題ぐらいです。円が関係するときは，中心角を求めるなど幾何的に考えるので，上記の技巧は使わずにそのまま図を把握することが大切です。

　さて，上記の技術の練習に使えるのが次の問題です。

　頻出の問題ですが，きちんと理解している生徒とそうでない生徒では解答時間に大きな差が生まれます。（解答例はこちら）

第2回は以上になります。自分はやたらと公式を数多く覚えて当てはめる練習をするより，少ない道具でも押し切るパワーと技術を身に着けさせたいと思って日々の指導にあたっています。その思想が垣間見える内容だったのではないでしょうか？

　次回はみんな気になる予備校講師の給料を暴露！共通テスト後の記述対策として，記述答案の書き方指導に役立つ話題を紹介したいと思います。引き続きよろしくお願いします♪