特集記事（高校）

神奈川県立横浜旭陵高等学校
持丸 裕一 先生

　確率の加法定理や余事象の確率，独立な試行の確率を学んだあと，これらの“内容のまとまり”を締めくくる大切な例題です。
　授業の核心は，「確率の計算で，たすときとかけるときの使い分け」に悩まないようにしてあげることですが，いままでの学習のつながりが感じられるような学び直しの場面（今回は余事象の確率の復習）もつくってあげたいものです。
　そこで，例題を解説したあとに，短い時間でねらいの達成につながる次のような発問をします。

　机間指導をしながら，例題通りに解く生徒と，余事象の考え方を利用して解く生徒を探して黒板に解答を書かせます。近頃はタブレットに書かせればすぐに共有できますね。

T -1：起こり得るすべての場合は，図のようになりますね。 　このうち，異なる色であるのは赤→白，白→赤で，同時に起こることはないから互いに排反です。場合分けしてそれぞれの事象が起こる確率を求めましょう。
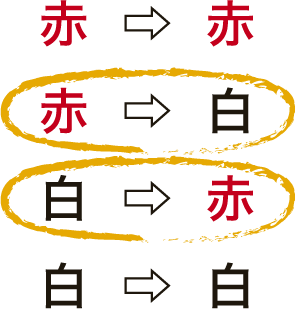T -2：球は元に戻すので，1回目の試行と2回目の試行は「互いに影響を与えない」，つまり独立です。
T -3：「これをして，引き続いて，これをする」とか「…かつ…」というときにはかけ算すればよいのでした。 　「1回目赤を取り出し，引き続いて，2回目白を取り出す」ので，かけ算！
T -4：「こんなときもある，あるいは，こんなときもある」とか「…または…」というときにはたし算すればよいのでした。 　「赤，白の順で出るときもある，あるいは，白，赤の順で出る時もある」ので，場合分けして，たし算！

　生徒の理解度によっては，別解を期待せず，ねらいを絞って次のような発問をします。

　授業の合間に設ける5分間のシンキングタイムに，生徒たちが自分の考えを表現し，他の生徒と意見交換することで，理解が深まるだけでなく，問いを持つ力も育まれます。また，先ほどの発問に対する解答も，生徒に説明させれば，表現力もつきます。

「色を3色にしても同じように求められるの？」
「少なくとも1個赤球が出る確率は？」
「色を確かめてからもとに戻さない場合の確率は？」

といった発問が生徒から出てくれば，シンキングタイムも延長大歓迎です。
　このような発問を通じて，生徒たちが自ら学び，成長する姿を見られることは大きな喜びです。ペア学習などを取り入れれば，協働的な学びが促進され，より楽しい授業になることでしょう。