特集記事（高校）

NEW ACTION 編集委員会

　この記事では，大学の入試問題を【思考のプロセス】の視点から考えてみたいと思います。今回取り上げるのは，2024年に京都大学で出題された理系大問6です。

　なかなか一筋縄ではいかなそうな問題ではあります。しかし，このような一見難解な問題であっても，解答に至るまでのスモールステップを適切に設定することができれば，これまでに学習した手法に帰着させることができます。
　このことを，【思考のプロセス】では  段階に分ける  と表現しています。

　この問題の場合は，おおよそ次のようなステップを踏むことになると予想されます。

（※予想される本問の【思考のプロセス】はこちら）

　第一段では，\(a_k\) の整数部分が \(n\) 桁であることを，数式を用いて表現することから始めます。教科書では，与えられた数が何桁であるかを知るために，常用対数を利用することを学びます。
　しかし，この問題を解くためには，「なぜ常用対数をとることが桁数を知る手掛かりになるのか」についての根本的な理解が求められています。

　ここでは， 定義に戻る  ことにしましょう。\(a_k\) が \(n\) 桁であるとは，不等式

\(10^{n-1} \leqq a_k \lt 10^n\)

が成り立つことです。この不等式において，\(a_k=2^\sqrt{ k }\) であることを考慮すると，各辺の2を底とする対数をとることで，\(k\) の範囲として

\((n-1)^2(\log_{2} 10)^2 \leqq k \lt n^2(\log_{2}10)^2\)　…(1)

を得ます。同様に，\(a_k\) の整数部分が \(n\) 桁であり，その最高位の数字が1であることは，不等式

\(1 \times 10^{n-1} \leqq a_k \lt 2 \times 10^{n-1}\)

と表されるため，\(k\) の範囲は

\((n-1)^2(\log_{2} 10)^2 \leqq k \lt (n-1)^2(\log_{2}10)^2+2(n-1)\log_{2}10+1\)　…(2)

と求まります。この問題から，「桁数といえば，常用対数」という条件反射的な学習に対するアンチテーゼを感じます。

　第二段に進みます。ここで登場する \(N_n\) とは，不等式(1)を満たす自然数 \(k\) の個数です。
　しかし，不等式(1)の左辺と右辺が整数であることは限りなく期待できないため，直接的に \(N_n\) を求めることは難しそうです。

　そこで， 見方を変える  ことにしましょう。不等式(1)を満たす整数 \(k\) の範囲が \(A_n\) から \(B_n\) まで（ \(A_n\leqq B_n\) ）であるとします。このとき

\(N_n = B_n -A_n+1\)

です。ここで，\(A_n\) と不等式(1)の左辺がどのくらいずれているかを見積もると，不等式

\(A_{n}-1 \lt (n-1)^2(\log_{2}10)^2\leqq A_n\)　…(3)

が成り立つことがわかります。この不等式を \(A_n\) について解くと

\((n-1)^2(\log_{2}10)^2 \leqq A_n \lt (n-1)^2(\log_{2}10)^{2}+1\)　…(4)

が得られます。同様に，\(B_n\) についても，不等式(1)の右辺と比較することで

\(B_n \lt n^2(\log_2 10)^2 \leqq B_n +1\)

すなわち

\(n^2(\log_2 10)^2-1\leqq B_n \lt n^2(\log_2 10)^2\) 　…(5)

が得られます。このようにして得られた不等式(4)，(5)から，\(N_n\) の範囲として

\(n^2(\log_2 10)^2-(n-1)^2(\log_2 10)^2 -1 \lt N_n \lt n^2(\log_2 10)^2-(n-1)^2(\log_2 10)^2 +1 \)

ゆえに

\((2n-1)(\log_2 10)^2 -1 \lt N_n \lt (2n-1)(\log_2 10)^2 +1\)　…(6)

が分かります。

　不等式(2)を満たす自然数 \(k\) の個数 \(L_n\) についても，同様の議論を行うことができます。不等式(2)が含む自然数を \(C_n\) から \(D_n\) まで（ \(C_n\leqq D_n\) ）とするとき

\(L_n = D_n \ – \ C_n +1\)

であり，\(C_n\) と \(D_n\) はそれぞれ

\(C_n -1 \lt (n-1)^2(\log_2 10)^2 \leqq C_n\)

\(D_n \lt (n-1)^2(\log_2 10)^2 +2(n-1)\log_2 10 +1 \leqq D_n +1\)

を満たすため，\(L_n\) の範囲は

\(2(n-1)\log_2 10 \lt L_n \lt 2(n-1)\log_2 10+2\)　…(7)

と分かります。

　このようにして \(N_n\) と \(L_n\) の範囲が求まります。ここで，不等式(3)の「 \(\lt\) 」と「 \(\leqq\) 」の使い分けが難しく感じる生徒がいるかもしれません。そのような場合は，数直線を  図で考える  ようにすることで，どちらの不等号が等号付きであるべきかが判断しやすくなるでしょう。

　また，すぐ後に第三段でお示しするように，この問題のゴールは比 \(\dfrac{L_n}{N_n}\) の \(n \rightarrow \infty\) における極限を求めることです。そのことを念頭におけば，不等式(6)や(7)について，（定数項のずれ程度の）ずれや不等号の等号付きの有無については，結果的にそれほど問題にはなりません。しかし，そのことを把握した上で「うまく割り切った」答案を書くことができる生徒は極めて少ないでしょう。
　この問題の学習を通じて，生徒にとっては，微小な誤差をうまく極限計算の中に丸め込むよりも，不等式の範囲の処理を丁寧に行えるようになることを，目指したいと考えます。

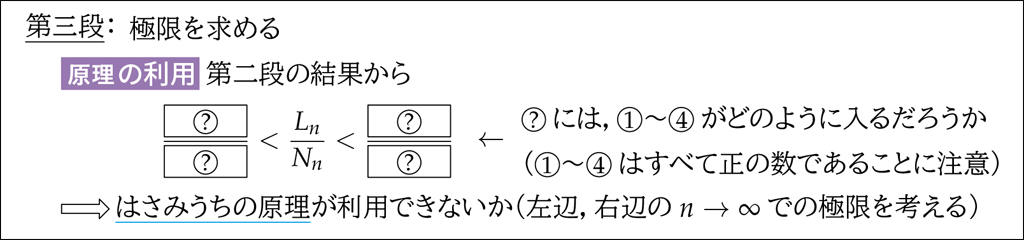
　さて，いよいよ第三段に進みましょう。不等式(6)，(7)を用いると，比 \(\dfrac{L_n}{N_n}\) のとり得る値の範囲が \(n\) の式として求まります。そこで， 原理の利用  として，はさみうちの原理を検討します。

　ここで，\(n \rightarrow \infty\) における極限を考えるにあたっては，\(n\) は十分大きな自然数として扱ってよいことに注意しましょう。そのような \(n\) においては，不等式(6)，(7)の左辺は明らかに正の数であるとしてよいため，比 \(\dfrac{L_n}{N_n}\) の範囲は

\(\dfrac{2(n-1)\log_2 10}{(2n-1)(\log_2 10)^2+1} \lt \dfrac{L_n}{N_n} \lt \dfrac{2(n-1)\log_2 10 +2}{(2n-1)(\log_2 10)^2-1}\)

と得られます。ここで，予想通り

\(\displaystyle \lim_{ n \to \infty } \dfrac{2(n-1)\log_2 10}{(2n-1)(\log_2 10)^2+1}= \log_{10}2\)

\(\displaystyle \lim_{ n \to \infty } \dfrac{2(n-1)\log_2 10 +2}{(2n-1)(\log_2 10)^2-1}= \log_{10}2\)

となることが確認できるため，はさみうちの原理により

\(\displaystyle \lim_{ n \to \infty } \dfrac{L_n}{N_n}=\log_{10}2\)

と求まります。

　これまでみてきたように，この問題では，一辺倒な学習では太刀打ちできないような仕掛けが施されています。しかし，【思考のプロセス】を用いた学習によって，対数や桁数に対する本質的な理解や不等式の適切な処理能力，特に整数の範囲の扱い方，そして極限の計算方法を身につけることができます。
　さらに，【思考のプロセス】を用いた学習は，これらの個別の内容に関する理解にとどまらず，問題を考えるために役立つ考え方をも身につけることができます。
　本問の解説を通じて，【思考のプロセス】が日常の学習を大学入試突破レベルにまで引き上げてくれることを感じ取っていただければ幸いです。

関連記事はこちら

＞【思考のプロセス】を活用した授業で，大学入試の答案作成に挑む