NEW ACTION編集委員会
はじめに
範囲や項目が限られた教科書の問題は解けるのに,入試問題にはまったく手が出ない。高等学校で数学の指導をしているとこのような生徒の声をよく耳にします。指導する側からすると「教科書の基本項目を理解して,それらを組み合わせることで入試問題にも対応できる」と思うのですが,数学が苦手な生徒からすると教科書と入試問題には大きな隔たりがあるようです。
NEW ACTIONシリーズはこの隔たりをどのようにして埋めるのかを考えて生まれた参考書です。本稿では,NEW ACTIONシリーズ,特にその大きな特徴である【思考のプロセス】を活用した授業例を紹介します。
【思考のプロセス】のヒントは板書にあり!
各例題の【思考のプロセス】は,“解法”の流れではなく“思考”の流れを,図を多用して示したものです。これまでの参考書では,解法の手順については箇条書きで示していました。しかし,これでは解法の手続きを把握することはできますが,別解の可能性や試行錯誤の過程を伝えることができませんでした。
【思考のプロセス】の編集にあたって参考にしたのは,実際の授業の板書です。上述の別解の検討や試行錯誤を含む思考の過程(考え方)について,指導者は必ず授業中に指摘・指導しているはずです。そして,その内容は板書に表れています。
ご採用いただいた学校の先生からは「授業の際の板書の参考にしています」というお声をいただきました。私たちの思いが伝わっているようでうれしい限りです。
【思考のプロセス】を用いた授業づくり
NEW ACTION シリーズを用いた授業づくりについて紹介しましょう。
まず,【思考のプロセス】の完成です。紙面の都合上,【思考のプロセス】は解答の最後まではカバーしていません。解答の道筋が立ったところで「手を離して」います。しかし,その先のプロセスを考えさせることもよい効果を生むのではと思います。数学の問題を題材にしたグループワークでも「【思考のプロセス】の完成」を課題とし,さらにその表現活動も含めることで充実した活動になるのではと思います。
次に,授業の板書を【思考のプロセス】スタイルにすることです。問題の解法を解説する授業の場合,板書が生徒の手元にある解答とほぼ同じ,解答の上に色チョークでポイントを付け加えながら授業を進めていくこともあると思います。これを【思考のプロセス】のスタイルに変えてみてはどうでしょうか。与えられた問題に対して「どのように考えるのか?」「どこに着目するのか?」「適切なプロセスワードは何か?」などに触れながら,【思考のプロセス】を黒板に完成させていく。そして,これを参考に,生徒に「答案」を作成させる。このような取り組みは,入試問題対策の際に必ず課題となる答案作成力向上にも有用ではないかと考えています。
【思考のプロセス】を活用した授業例
NEW ACTIONシリーズでは,1つの「例題」に対して,その類題である「練習」と応用問題である「問題」が対応しています。これらを段階的に利用して【思考のプロセス】を完成させる取り組みを,次の例題を例に考えてみましょう。
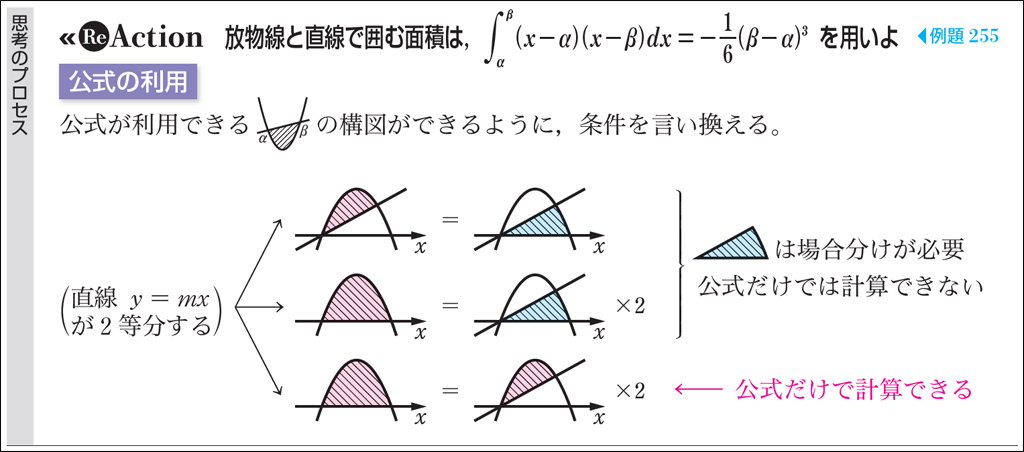
例題 263 は放物線とx軸で囲まれた部分の面積を2等分する直線の傾きを求める問題です。面積について条件を満たす方程式を立てる際に「どうすれば公式を効果的に利用することができるか」を考えることがポイントです。【思考のプロセス】ではあえて効果的とはいえない例も示し,試行錯誤の過程を示しています。
この解法を理解した後に,問題263に挑戦させます。
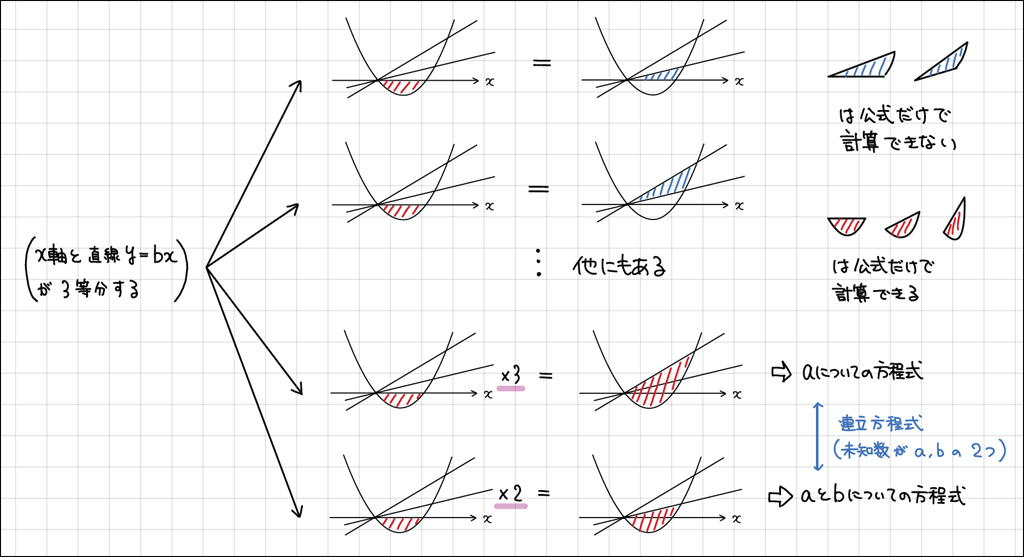
問題263は,放物線と直線で囲まれる部分の面積をx軸と直線で3等分するとき,放物線の方程式の係数と直線の傾きを求める問題で,例題と同じ設定ですが変数が増え,難度が増しています。
ここで,そのまま答案を作成させるのではなく,例題263の【思考のプロセス】に倣って,問題263の【思考のプロセス】を考案させてはどうでしょうか。
このように,「問題」の多くがそれに対応する「例題」の【思考のプロセス】を参考にすることで,新たな【思考のプロセス】を考案することができます。難易に差がついた同じ内容の2題であるからこそ,このような学習が実現できるともいえます。
入試問題の答案作成にチャレンジ
入試を控え,答案の作成を指導する際に「数式のみしか書かない答案」の指導に苦労することがあります。指導者からすると,計算を示すよりも考え方を論理的に表現してほしいと思うところです。
答案作成中の生徒の様子を観察していると,下書き用紙(計算用紙)と答案の区別がついていないように感じることがあります。模擬試験や入試問題においても,本稿で紹介した【思考のプロセス】を考える活動を手がかりに,下書き用紙には【思考のプロセス】のように思考の流れをまとめ,それを参照しながら答案を作成していくことができないかと思っています。思い付いたままに計算を羅列するのではなく,「数式と数式の間を繋ぐ文章」を適切に補った答案の作成には,【思考のプロセス】を含む下書き用紙の効果的な使い方が重要ではないでしょうか。
その他のコンテンツ