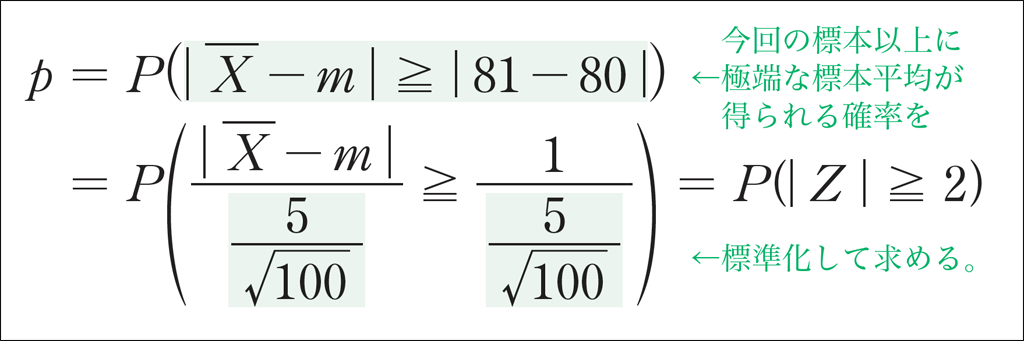(前編はこちら)
【信頼度95%の信頼区間】
母分散が \(\sigma ^2\) のとき,母平均 \(m\) に対する信頼度95%の信頼区間は,次の式で表されます。
\(\overline{ X } \ – \ 1.96 \cdot \frac{\sigma}{\sqrt{ n }} \leqq m \leqq \overline{ X } + 1.96 \cdot \frac{\sigma}{\sqrt{ n }}\) …①
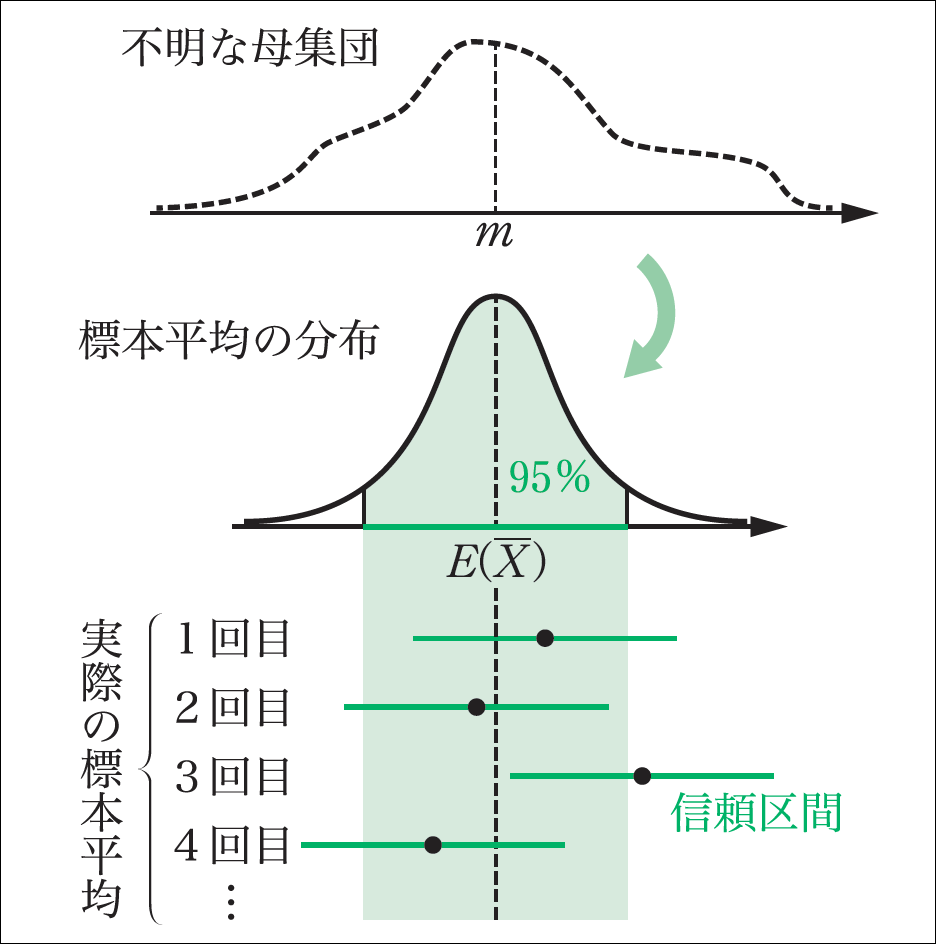
信頼区間を用いた推定における関心は母平均ですが,大数の法則により母平均 \(m\) と標本平均 \(\overline{ X }\) の平均 \(E(\overline{ X })\) は一致します。よって,①で表される区間は,“95%の確率で \(E(\overline{ X })\)を含む 区間”と言い換えることができます。
このことから,標本平均 \(\overline{ X }\) の確率分布において \(E(\overline{ X })\) を中心に95%が分布する区間の幅が,そのまま信頼度95%の信頼区間の幅となることが,次の図からも見てとれます。
さて,信頼区間の学習において鬼門となるのは“95%”の解釈です。次のような例え話を考えてみましょう。
Aさんを含む100人の生徒が,同じ母集団から標本を抽出し,公式に従って95%の信頼区間を求めるという作業を,生徒ごとに行うとします。
標本を抽出する前,Aさんが求める信頼区間が真の母平均を含む確率は“95%”です。
しかし,Aさんが標本を抽出して求めた具体的な区間は,真の母平均を含むか否かのいずれかですが,どちらかは分かりません。
一方で,100人の生徒全体で見ると,求めた区間に真の母平均を含む生徒が(近似的に)95人程度いるはずです。その意味では“95%”は割合です。
このことから,Aさんは「自分が求めた区間に,真の母平均を含んでいる可能性は高いだろう」と推論することができます。そして,その推論の信頼度が“95%”となります。
実際の標本調査では,予算や時間などの都合で標本抽出が1回しかできないこともあり,得られた信頼区間を,信頼度という考え方で解釈するのです。
仮説検定の全体像と評価のポイント
【正規分布と標準化】
初学者にとって,仮説検定の全体像を把握するのは容易ではありません。仮説を自ら設定したり,得られた結果を解釈して判断を下したりする点も独特ですが,問題から結論までの手続きが多い点もその要因となっています。
さて,統計的手法を用いた問題解決の手順に,問題(Problem),計画(Plan),データ(Data),分析(Analysis),結論(Conclusion)の5段階からなる“PPDAC”サイクルがあります。
生徒は,小学校・中学校の統計の学習で幾度もPPDACに触れています。仮説検定の全体像が理解しにくいときは,このPPDACの枠組みを利用して整理することで,見通しがよくなるかもしれません。
ここでは,実際の問題をPPDACの枠組みに当てはめながら,仮説検定の指導と観点別評価のポイントについて整理してみましょう。
これをPPDACの枠組みで整理すると,次のようになります。
| 問題: | 今月製造したお菓子1 袋の重さは基準通りといえるか。 |
| 計画: | 帰無仮説を \(m=80\) とし,大きさ100の標本を抽出して,有意水準5%で両側検定する。 |
| データ: | 標本の平均は81gであった。 |
| 分析: | 帰無仮説に基づいた標本平均の分布において,得られたデータ以上に極端な結果が得られる確率を求める。(計算すると約4.6%) |
| 結論: | 有意水準と比較して帰無仮説を棄却し,お菓子1袋の重さは基準通りでないと判断する。 |
この5段階のうち,生徒が能動的に関わるのは,計画,分析,結論の段階です。それぞれについて,詳しく見てみましょう。
【計画:分析と結論のための前提をつくる】
計画は,分析の枠組みを決め,結論を下すための基準をつくる段階であることを意識するのが大切です。必要なのは,有意水準と検定の方法(片側か両側か),帰無仮説と対立仮説です。
目的に沿った仮説を設定し,それを数学的に表現できるかどうかが,評価の観点(思考・判断・表現)のひとつになります。
【分析:操作と式の意味を意識する】
分析は,仮説に基づいた標本平均の分布を求め,標準正規分布と有意水準を用いて,得られたデータを正しく評価できるかどうかが,評価の観点(知識・技能)のひとつになります。
ここで注意をしたいのが,棄却域を利用した解法です。
得られた標本の平均 \(\overline{ x }=81\) を標準化した値
\(z=\dfrac{81-80}{\frac{5}{\sqrt{ 100 }}}=2\)
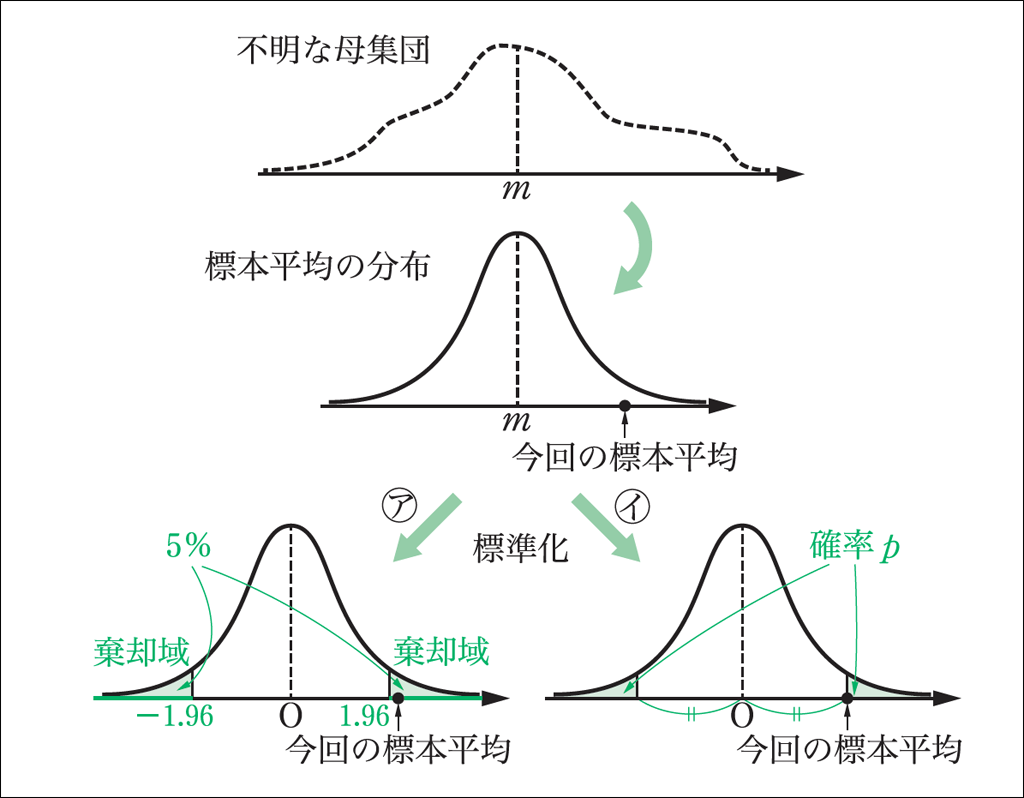
が,両側検定の棄却域 \(|Z|\geqq 1.96\) に含まれるかどうかで,簡便に帰無仮説について判断できます。(前図㋐)
しかし,この方法は,本来の仮説検定の手順である「得られたデータ以上に極端な結果が得られる確率\(p\)と有意水準を比較する」(前図㋑)とは直接対応していません。時間が経てば,なぜ棄却域で帰無仮説を判断できるのか,操作や式の意味が曖昧になる恐れもあります。
本来の手順である確率\(p\)を求める式も,その意味と対応させて理解しておくとよいでしょう。
これと,有意水準 \(P(|Z|\geqq 1.96)=0.05\) を比較します。
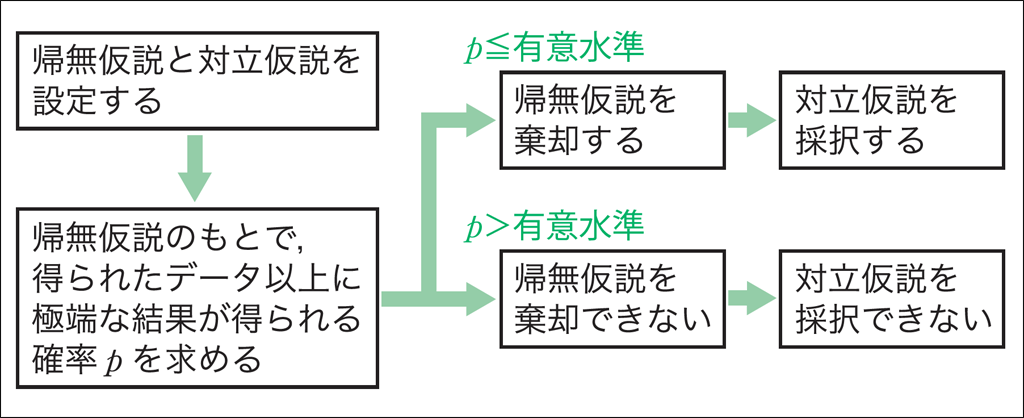
【結論:“仮説検定の考え方”で判断する】
設定した仮説について,得られたデータから正しく推論し結果を解釈できるかどうかが,評価の観点(思考・判断・表現)のひとつになります。
背理法的な“仮説検定の考え方”の論理はやや独特であり,数学Bは分析における計算の負担も大きいため,やはり数学Ⅰの「データの分析」で,あらかじめ“考え方”をしっかり押さえておくことが大切になるでしょう。
帰無仮説について判断をする際は,単に「棄却する」だけでなく,「有意水準5%の両側検定のもとで棄却する」として前提もあわせて捉えると,結論の根拠が明瞭になります。
〈了〉
その他のコンテンツ