特集記事（高校）

数学Advanced・Standard 統計分科会

図や具体例を用いて理解を促す

【正規分布と標準化】

　正規分布は，確率変数を標準化して標準正規分布にすることで，諸々の確率を求めることに利用できます。機械的に標準化してしまいがちですが，分布をどのように操作しているかは，理解しておくとよいでしょう。
　次の問題を例に考えてみます。

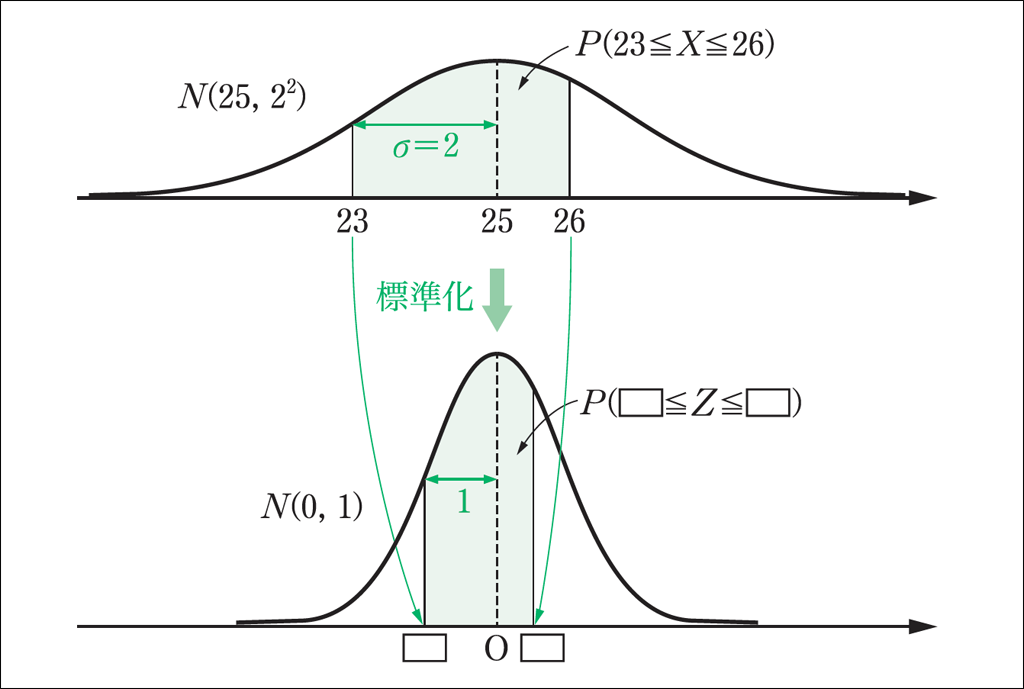
　平均25，標準偏差2の正規分布に従う確率変数を\(X\)とすると，求める割合は，確率\(P(23 \leqq X \leqq 26)\)と一致します。
　しかし，これを直接求めることはできないので，\(X\)を標準化することを考えます。
　\(Z=\frac{X-25}{2}\)とすると，確率変数\(Z\)は標準正規分布\(N(0,1)\)に従います。これは，\(X\)の分布曲線を

• \(x\)軸方向に－25だけ平行移動する
• 曲線の対称軸を基準に\(x\)軸方向に\(\frac{1}{2}\)倍する
• \(\int_{-\infty}^\infty f(x)dx=1\)となるように，\(x\)軸を基準に\(y\)軸方向に2倍する

ことで，標準正規分布の分布曲線に一致させる操作です。

　数学Ⅲの内容にはなりますが，これらは正規分布を与える確率密度関数\(f(x)\)の式

\(f(x)=\displaystyle \frac{1}{\sqrt{ 2\pi }σ}e^{ \tiny{\displaystyle – \frac{( x – m )^2}{2σ^2} } }\)

における\(\sigma\)の役割からも見てとれます。
　なお，\(x=m+σ\)，\(x=m-σ\)に対応する曲線 \(y=f(x)\)上の点は変曲点です。図示の際の手掛かりになります。
　以上より，\(X=23,26\)のそれぞれに対応する\(Z\)の値を求めることで，正規分布表を用いて，\(P(23 \leqq X \leqq 26)\)を求めることができます。

【標本平均の分布と中心極限定理】

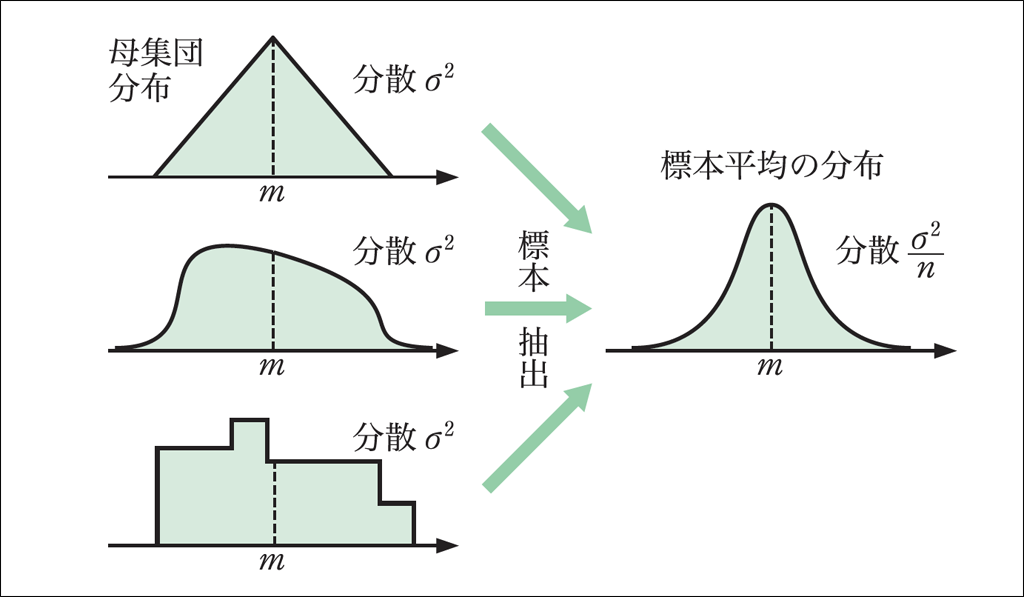
　母集団の分布によらず，標本の大きさが十分大きければ，標本平均の分布は正規分布に近似できます。この性質を中心極限定理といい，正規分布が統計学において重要な位置を占める理由でもあります。中心極限定理は，推定や検定といった章の後半の学習を支える基礎です。

　とはいえ，中心極限定理が示す結果は，私たちの直感とはやや距離があり，一般化された導出だけではイメージしにくい面もあります。
　そこで，具体的な例やシミュレーションを通して，定理の威力を実感してみましょう。

　ここで，\(X_1,X_2, \cdots, X_n\)を母集団から抽出した標本とします。標本平均は

\(\overline{X} = \displaystyle \frac{X_1+X_2+ \cdots +X_n}{n}\)

で求められます。このとき，確率変数\(\overline{X}\)が正規分布に従うことより，和\(X_1+X_2+ \cdots +X_n\)も正規分布に従うことが分かります。

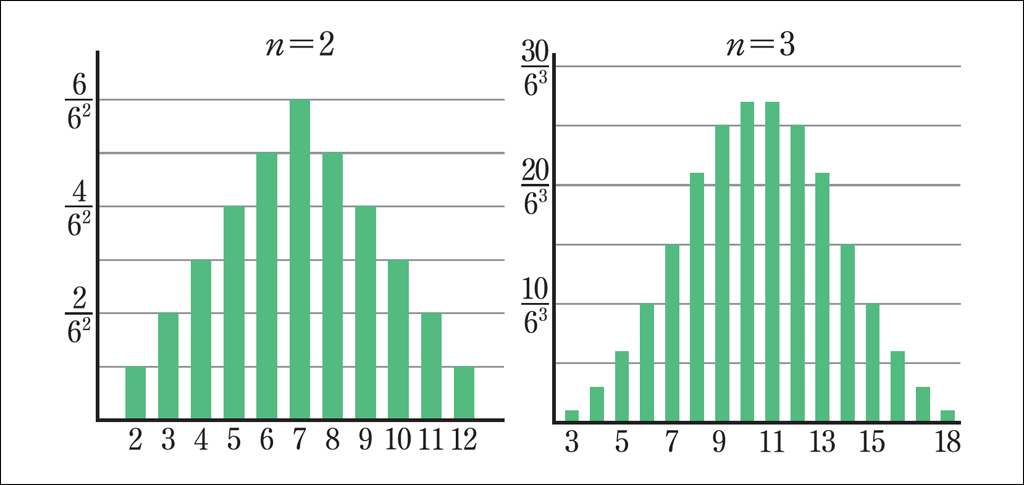
　さて，一般的な六面サイコロを2回振って出た目の和を考えてみましょう。これは，1 から6までの確率変数の値がすべて等確率に分布する母集団から，大きさ2の標本を取り出すことと同じです。
　2つの目の和を確率変数とすると，その確率分布は次の左図のようになります。生徒も，場合の数を用いて自力で求めることができるでしょう。

　母集団分布が一様のため，標本の大きさが2であっても，既に正規分布を思わせる山なりの分布が見て取れます。
　加えて，標本の大きさが3，すなわち，サイコロを3回振って出た目の和の確率分布（先の右図）が，さらに正規分布に近づく様子を見れば，中心極限定理の威力が実感できるでしょう。

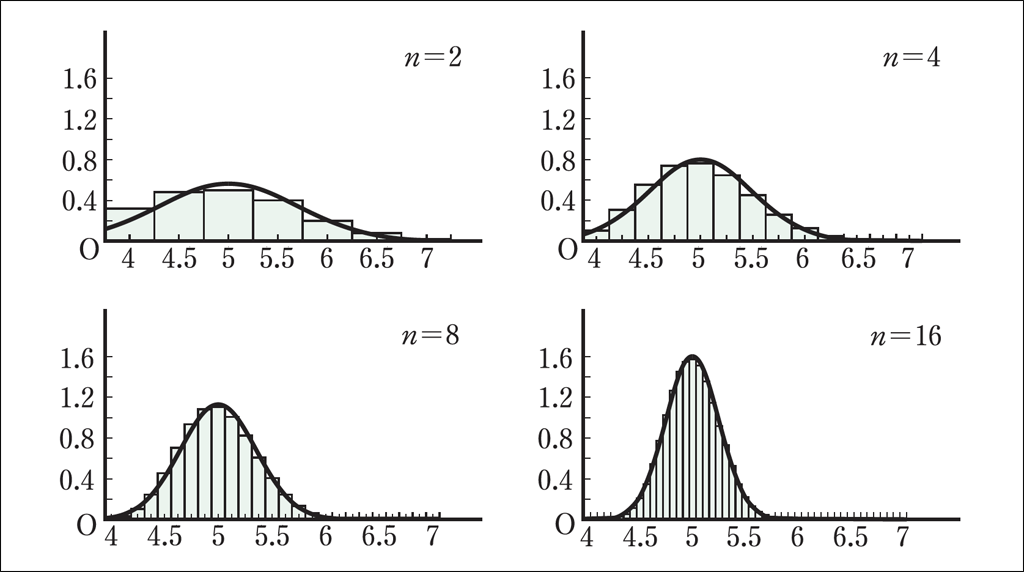
　もちろん，母集団分布に歪みがあっても中心極限定理は成り立ちます。このことを実感するには，実際にシミュレーションをしてみるのがよいでしょう。
　例えば，次の表のような分布の母集団から，

大きさ\(n\)の標本を取り出したときの標本平均の分布は，次のようになります。

　必要であれば，このシミュレーションが可能なMicrosoft Excel ファイルをこちらからダウンロードできます。ご活用ください。
　様々な数値を設定してシミュレーションをすると，一般に，母集団分布の歪みが大きいほど，標本平均が正規分布に近似するために，より大きな標本が必要であることが伺えます。
　このことから，分布が不明な母集団から実際に標本を抽出するときは，ある程度の大きさの標本を確保することが非常に重要であることが理解できます。

※後編では，「信頼区間の意味」，「仮説検定の全体像と評価のポイント」を取り上げます。