特集記事

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　今回は、若手の先生からいただいた困り事について、考えてみたいと思います。

学習評価の工夫を考える 〜「主体的に学習に取り組む態度」編その①

Q　「主体的に学習に取り組む態度」の評価について悩んでいます。生徒のノートやレポート、テストなど様々な方法があるとは思うのですが、実際にはどうすればよいのでしょうか。

Ａ　次のポイントを意識してみましょう。

単元の指導計画を考える際に、教科書等を見て評価場面と評価として期待する姿の具体を検討する

　夏休みが終わり、いよいよ新学期のスタートですね。これまで、数学的に考える資質・能力の育成を目指すための学習評価について考えてきました。これまでは、観点別評価の「知識・技能」「思考・判断・表現」について紹介してきました。

　今回は「主体的に学習に取り組む態度」の評価です。現行の学習指導要領から、「関心・意欲・態度」から変更されています。この学習評価について、どのように取り組めばよいでしょうか。

　従前の「関心・意欲・態度」の観点では、授業で発言した回数や課題（宿題）やレポートの提出状況の把握が評価の根拠とされることが問題視されました。生徒が毎日の学習の取り組みに積極的な関わりを見せていることはとてもよいことですし、むしろ、褒めてあげたいですね。しかし、数学を学習しているということは、“数学への態度”について評価すること本来ではないかということが指摘されるようになり、今に至ります。「主体的に学習に取り組む態度」の評価には、下のような2つの側面があると言われています。

　この2つの側面は相互に関わり合いながら立ち現れるものであり、このことについて生徒の学習の様子を観察し、評価として判断することが求められています。また、実際の評価では、この2つの側面の有無を確認することのみにならないように留意し、学習の調整が知識及び技能の習得に結びついていない場合には、学習の進め方についてまれに指導することも必要です。

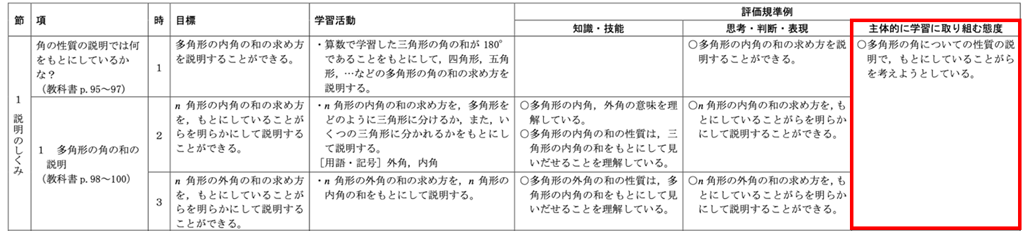
　さて、「主体的に学習に取り組む態度」の評価について具体的に考えてみましょう。この観点の評価を進めるための方法としては、ノートやレポート等における記述、授業中の発言、教師による行動観察や生徒による自己評価の状況等を、評価を行う際の材料として用いるために記録することが必要です。このことは行き当たりばったりとならないように、単元の指導計画を考える際に場面や、学習の調整についての具体を想定しておく必要があります。 下の表は、東京書籍が公表している令和3年度年間指導計画作成資料数学科の「2年学習指導計画・評価規準例」の一部です。これを例として考えます。

https://ten.tokyo-shoseki.co.jp/text/chu/list/keikaku.html

　節「1説明のしくみ」は、新しい数学2のp.95〜100に掲載される多角形の角の和について性質を見いだし、それが成り立つことを説明する学習内容です。多角形の内角の和は、小学校算数第5学年の学習を受けて、さらに、多角形の内角から外角へ見方を拡げてその和を論理的に考えます。上の表の右（赤枠）には、「多角形の角についての性質の説明で、もとにしていることがらを考えようとしている。」が3時間にわたって記載されています。しかし、3時間全てで評価すればよいということでもありませんので、指導される先生が単元全体を見渡して必要な程度を検討し判断するとよいです。

また、評価規準には「もとにしていることがら」と表され、これは1、2時間目については「三角形の内角の和」、3時間目は「多角形の内角の和」をそれぞれ意味し、既に認めた数学的な事実（事柄）のことを用いることで問題解決しようとする態度を評価することが考えられます。このように評価の対象となる数学への態度について具体化し、それを記録して残すのか、あくまで生徒の学習状況の過程として観察することにとどめるのか事前の判断が必要です。

さらに、記録として残す場合には、生徒のノートから読み取るのか、振り返りの場面での記述とするのかについても検討しましょう。 もう少し具体的に考えてみましょう。下の紙面は、新しい数学2 p.100にある「多角形の外角の和の求め方の説明」の一部です。ここでは、多角形の内角から外角に着目を変えて、その和を求める方法について考察します。多角形の外角という用語については前時に確認済みです。

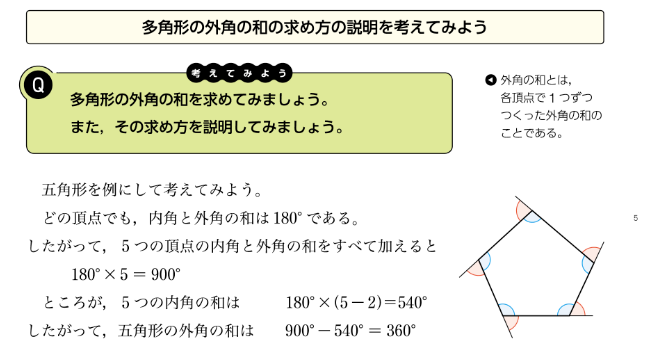
　多角形の外角の和について考える授業では、五角形を例にして「五角形の外角の和を求めるためにはどのような方法があるだろうか」と見通しや構想を立てる場面を設定します。すると、分度器で測ればよいと述べる生徒もいるでしょう。それを否定せずに、「測らなくても分かるものなのかな」と問い返すことで、既に認めた数学を関連付けようとする姿として、「学んだことを使えないか」「多角形の内角の和の性質が使えるかも」などを期待します。各個人の評価とはなりません、黒板に板書して学級で全体での解決の見通しとして確認するとよいでしょう。

　解決場面では生徒がどのように取り組もうとしているかについて観察します。「五角形の外角の和をどのようにして明らかにしようとしているのか」などと問いかけ、問題解決への生徒の粘り強さや自己調整についての状況を把握することができます。このことは、生徒全員には無理かもしれないことから、記録に残す評価としては難しいです。しかし、観察して得られたことをメモしておくことで、授業を進める際の役立つ情報となりますし、最後の振り返りの場面の際に問題解決の過程として紹介し、数学への態度について学級で共有することができるでしょう。

　観察を中心とした「主体的に学習に取り組む態度」の状況把握について紹介しました。次回は「記録に残す」ことについて、みなさんと一緒に考えてみたいと思います。

※参考資料

• 「指導と評価の一体化」のための学習評価に関する参考資料 中学校数学
• 東京書籍 「新しい数学2」

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。