特集記事（小中学校）

「佐藤寿仁先生と考える」では、授業づくりのポイントや教科書の使い方などについて、連載していきます。現場の先生方は、大変お忙しくて教材研究する時間が取りにくいところかと思います。少しお時間をいただき、立ち止まって一緒に考えてみませんか。（佐藤寿仁）

　前回から引き続き、若手の先生からいただいた困り事について考えてみます。今回は「自力解決や比較・検討の場面を考える」の前編となります。

自力解決や比較・検討の場面を考える 〜場面設定の工夫〜

Q　自力解決や比較・検討の場面について、大切なポイントはありますか？

Ａ　次の3つのポイントを意識してみましょう。

1. ① 個と集団の学びを授業に位置付ける際の目的を明確にする
2. ② 個や集団での学び場面を柔軟に考え、比較・検討を充実させる
3. ③ 教科書を活用して、個や集団の探究的な学びを加速させる

　数学の授業では、生徒の問題解決を大切にしています。自力解決や比較・検討の場面を工夫することで、主体的な問題解決を支えることができます。現行学習指導要領においては、指導される先生方の、授業改善の視点を「主体的・対話的で深い学び」としています。問題解決には、集団において協働が求められ、それを進めるためには対話はなくてはならないものです。
　授業では、先生が何もせず、全てを生徒たちで進めることはありません。学年が上がるにつれて、だんだんと先生の手を離れ、自律した学習者となることは大切なことですし、そのような成長を目指します。今回は、そのために自力解決や比較・検討の場面設定での工夫について紹介します。
　「新しい数学1」1章「正負の数」における「正負の数の利用」の第1時（p.55,56）を例に考えてみましょう。

①　個と集団の学びを授業に位置付ける際の目的を明確にする

　導入場面において、問題把握をして解決の結果や方法について見通しや構想を立てて考えた後に、自身で解決を図る「自力解決」の場面が設定されることがあります。

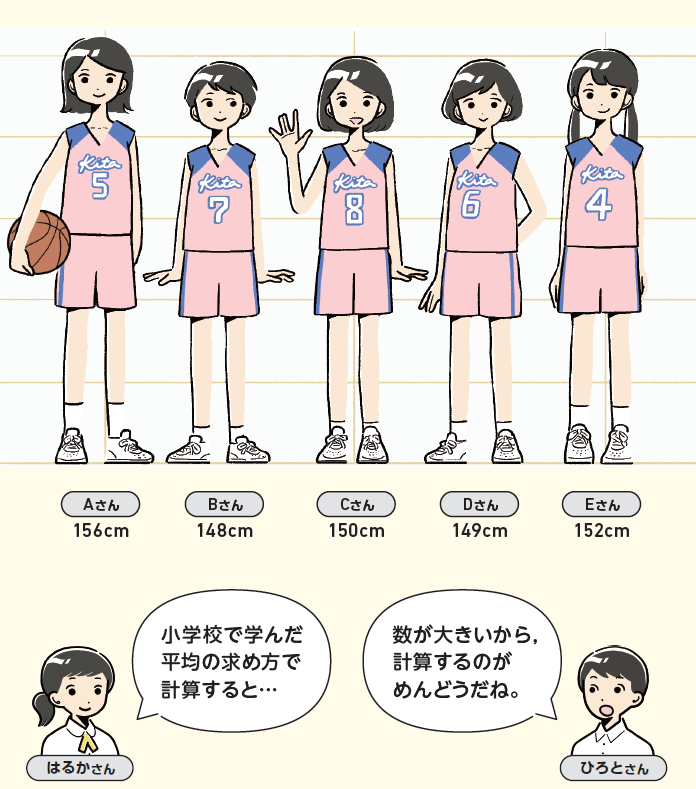
　ここでは、見通しとして、小学校算数での平均の求め方を振り返ります。そして、5人の身長の値を確認し、その値の大小に着目することで、「計算がたいへんそう」「電卓があれば楽なのに…」などが生徒から挙げられるでしょう。たしかに電卓を使えば、簡単に計算できますが、「電卓を使わないで考えるとしたら…」のように投げかけて平均を工夫して求めるという本時に解決すべきことを確認します。そして…、

　「まず、自分一人で考えてみましょう」

　自力解決が始まります。そもそも、どうして自力解決の場面があるのでしょうか。「話し合いの場面の前に、自分でやってみる時間があるのが普通」と考えて授業の型のようにしてはいませんか。自力解決で、すべての生徒が解決できるというわけではありませんが、自分の考えを持つことは大切です。「自力解決」は自分なりに考えて問題解決をする多様な個の学びの場面です。

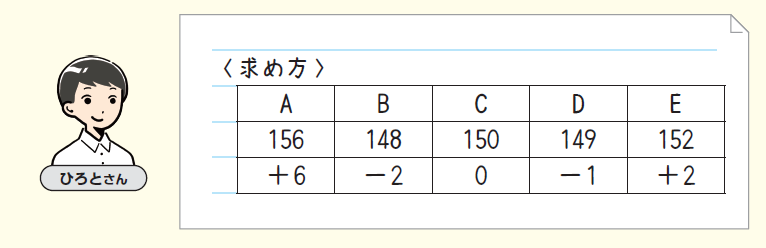
　教科書p.56のひろとさんのように、Cさんの身長150cmを基準にして正負の数を用いて考える生徒がいると思います。このほかにも最小の値であるBさんを基準にする生徒もいるかもしれません。基準をどこに設定しても平均を求めることができるので、自力解決では自分なりに考えた目的でいろいろな値を基準として平均を計算することを期待します。

　しかし、自分で考えることが困難な生徒もいます。自力解決の場面では、どこまで考えることができているか、何で困っているかなど生徒の状況を把握することも大切です。手が止まっている生徒は問題が把握できているかなどを確認することも考えられます。

　「さあ、グループをつくって、みんなで考えてみましょう。」

　授業の場面は、自力解決から話し合いへと移ります。生徒が話し合う場面を設定する際に、どのくらいの時間で設定すればよいかについて悩みますよね。「話し合いの場面にかける時間は○分間」という一般的なきまりはありません。そのことよりも、まず、生徒が問題解決するために話し合いの場面では「何を・どこまで・どんなふうに」話し合うのか、話し合いのゴールを先生が明確にしておくことが大切です。

　教科書P.56の平均の求め方の工夫を考える話し合いでは、例えば、次のようなゴールが考えられます。このことから、どのくらい時間がかかるかを予想し、話し合いの時間を設定するとよいでしょう。

• 何を … 結果（身長の平均は151cm）は同じであること。個人で考えた平均の求め方の具体。
• どこまで … 平均の求める方と、設定した基準の値。
• どんなふうに … 基準を用いて平均を求める式を互いに解釈する。

　前編は、自力解決や比較・検討の場面の下の3つのポイントのうち①について考えてみました。

1. ① 個と集団の学びを授業に位置付ける際の目的を明確にする
2. ② 個や集団での学び場面を柔軟に考え、比較・検討を充実させる
3. ③ 教科書を活用して、個や集団の探究的な学びを加速させる

後編では②、③について考えてみます。

【佐藤寿仁先生　略歴】
岩手県公立中学校で11年、岩手大学教育学部附属中学校で6年教職を務め、岩手県岩泉町教育委員会指導主事、国立教育政策研究所学力調査官・教育課程調査官を経て、令和3年度より岩手大学教育学部准教授。学校教育の充実や現職教員の職業能力開発の支援から、全国調査など国の教育のアセスメントに関わり、これからの教育について幅広く研究を進めている。