特集記事（小中学校）

　第5回の配信は、新しい算数教科書の新ページについてです。
　自ら課題を見出し、問題解決する児童を育むためにはどのような手立てが必要でしょうか？
　「新しい算数」編集委員会では、これまでの問題解決の過程を振り返り、新たな課題を見出し、解決の計画を立て実行することを促す新ページ、「それなら次は？」を生み出しました。
　「それなら次は？」は、第3回の配信でご紹介した新キーワード「同じように考えると」と「それなら」と深く繋がりを持ち、「自分たちで学習を切り拓く」ことをテーマとしています。

　本記事では、新ページ誕生の経緯、一例についてご紹介します。

➡　新しい教科書のキーワードのひみつ　はこちら

新ページ誕生の経緯
〜「それなら次は？」\(=\)「同じように考えると」\(\times\)「それなら」〜

　今、子どもたちには、算数に閉じない未知の問題に出会った際、それまでに獲得したものの見方・考え方を働かせながら、既有の知識・技能や思考力を生かして解決する力をつけることが不可欠です。
　「今、求められるこの力の育成に算数教科書も貢献すべきだ」という編集委員会全会一致の考えのもと、紙面を具現化するための議論を重ねました。
　実は、議論の過程では、まず、育成のためのページとして「それなら次は？」の構想が提案されました。そして、議論を掘り下げるなかで、育成すべき力を「前の学習と今の学習を統合したり関連付けたりすること」と「今の学習を生かして次の学習を創り出すこと」と因数分解的に捉え、「それなら次は？」の素地となるそれぞれの力を適宜育成できるような全体構成が望ましい、という結論となりました。
　つまり、「それなら次は？」を構想する過程で、「同じように考えると」、「それなら」が誕生したのです。
　数学らしく表現すれば、

「それなら次は？」\(=\)「同じように考えると」\(\times\)「それなら」

というイメージです。

自ら課題を見いだし、計画を立て、解決する

　5年下p.55では、台形やひし形の面積について学習します。今日の学習までに、長方形や平行四辺形、三角形の面積について学習しています。

　ページの上段にご注目ください。ここでは、これまでの学習を振り返り、この後の学習計画を立てます。
　まず、これまでの学習を振り返り、台形とひし形の公式を求めていないことを明らかにします。
　次に、学習した平行四辺形と三角形の面積を考えた３つの過程（①面積を求める、②使う長さを考える、③公式をつくる）、ポイントとなる見方・考え方を確認します。
　その上で、児童自らが台形、ひし形の面積の公式をつくる計画を立て、その計画に沿って公式について考えていきます。

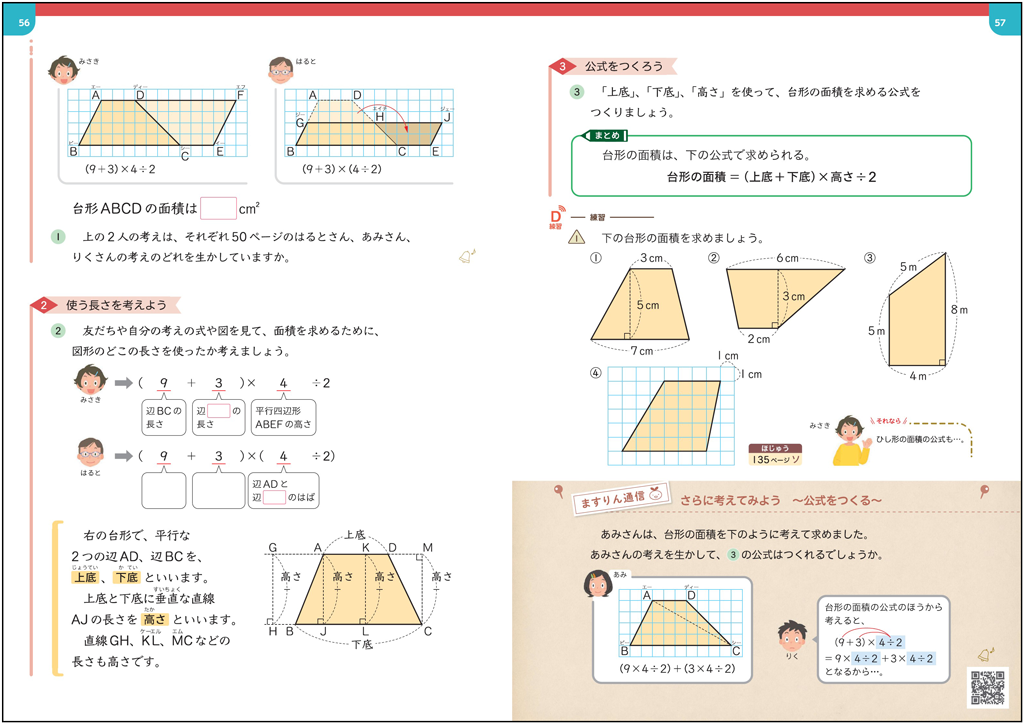
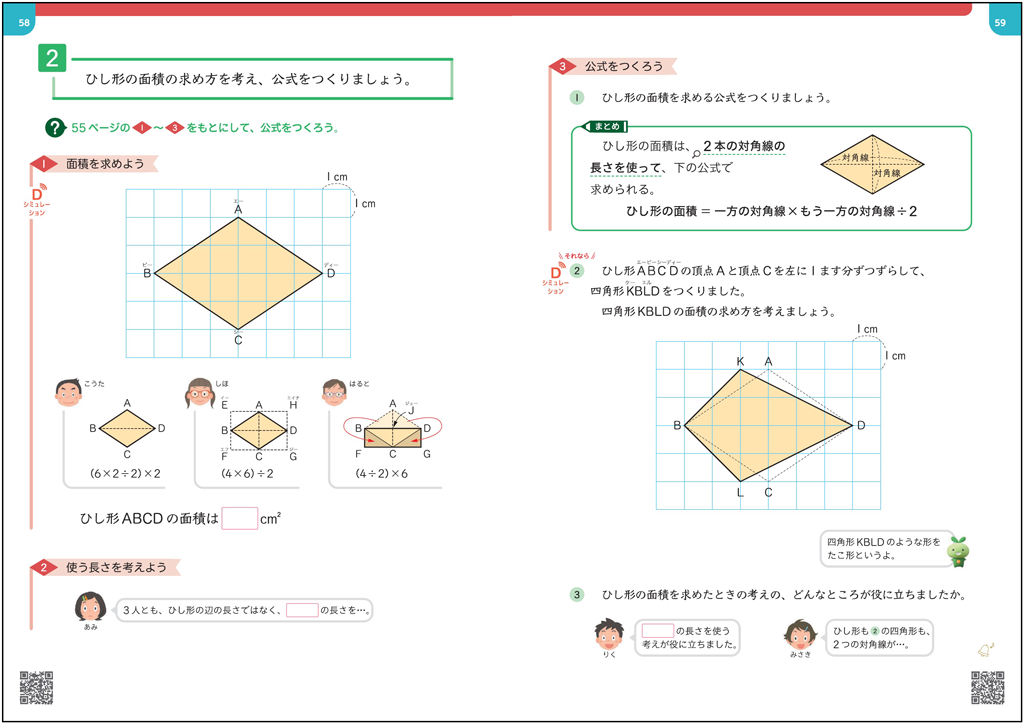
　ページの左側では、導入時に立てた計画のどこに当たるのかをラインで示し、常に計画を意識できるようにしました。
　また、教科書全体を通して、単元の前半はこれまで通り丁寧に記述し、中盤から後半にかけては記述をシンプルにしました。単元の終盤となる本学習では、吹き出しの内容を精選し、児童がこれまで培った力を発揮して解決できるようにしています。

自分たちで学習を切り拓く

　このように、算数の学習を通して、自ら課題を見いだし、学びをつなぎ、計画を立てて解決するという汎用的な力を育むことを願い、新ページを設けています。
　今回の新ページは3年以上に新設しています。ぜひ新ページ「それなら次は？」にご注目ください。

　ここでご紹介した“ひみつ”以外にも「新編 新しい算数」の魅力はまだまだ他にもあります。ぜひバックナンバーもご覧ください。

「新編 新しい算数のひみつにせまる」バックナンバーは こちら

　令和6年度用教科書「新編 新しい算数」特設サイトでは、ここでご紹介した特長のほかにも新しい教科書の情報を掲載しています。ぜひ一度、サイトをご覧ください。

特設サイトは こちら