特集記事（小中学校）

　第3回の配信は、新しい算数教科書の新キーワードについてです。
　現行学習指導要領では、「統合的・発展的に考える」ことが目標の一つとして示され、「思考力・判断力・表現力等の育成」の中の重要な要素として位置づけられています。これは、これまでも先生方が大切にされてきた価値観でもあり、教科書の改訂にあたり、より一層のブラッシュアップを目指しました。
　「統合的・発展的に考える」とはどのようなことでしょうか？「新しい算数」編集委員会では、今の学習を、前の学習やこの先の学習とつなぐことと捉え、前の学習とつなぐキーワードとして「同じように考えると」、次の学習へのつながりをつくるキーワードとして「それなら」を紙面に付記しました。

　本記事では、新キーワード誕生の経緯、一例についてご紹介します。

新キーワード誕生の経緯

　既習を活用して問題解決すること、統合的・発展的に考えることは、これまでの教科書でも扱っていましたが、子どもたちが意識しにくい部分もありました。そこで、子どもたち自身が、より主体的にこのような考え方をできるように、「同じように考えると」「それなら」といった子どもらしい表現で、朱文字でハッキリと明記しています。

「前の」学習とつなぐ「同じように考えると」

　5年下p.49では、三角形の面積の求め方について学習します。今日の学習までに、長方形や平行四辺形の面積については既に学習しています。

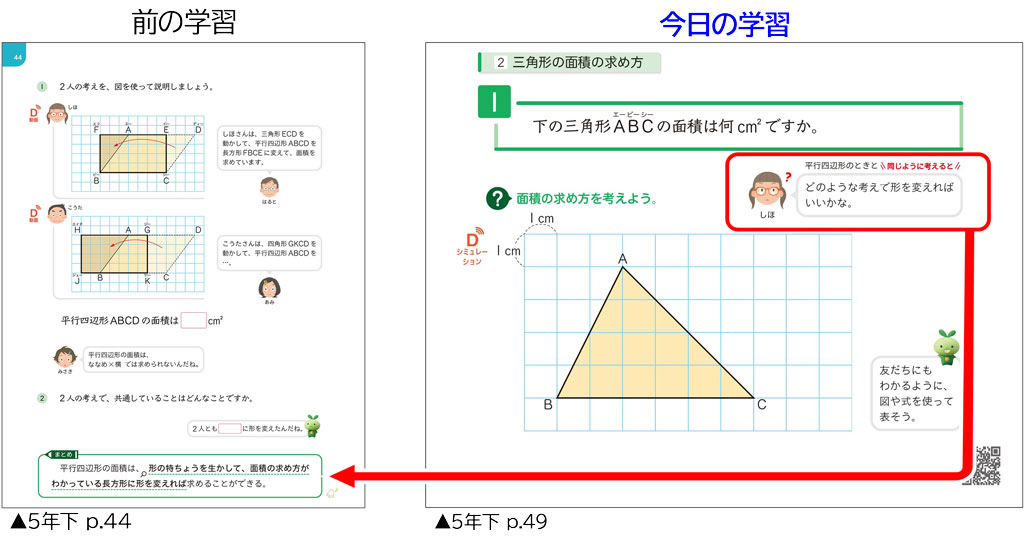
　三角形の面積の求め方を考える問いに対するしほさんの吹き出しにご注目ください。ここでは、前の学習で、平行四辺形の面積を、既習の長方形に変形して求めたことを想起させ、三角形の面積を求める上でも”同じように考えられないか”と促します。
　さらに、”同じように考えると”は、「既習の知識・技能及び考え方を活用することを促す」までにとどめ、吹き出しの内容は現行教科書と比べてシンプルにしています。吹き出しの続きを、子どもたち自身が考えられる余地を残しているので、子どもたちの力を発揮して解決していくことができます。

「次の」学習とつなぐ「それなら」

　そして、5年下p.50では、上記の三角形の面積を求める学習をまとめで確認することができます。

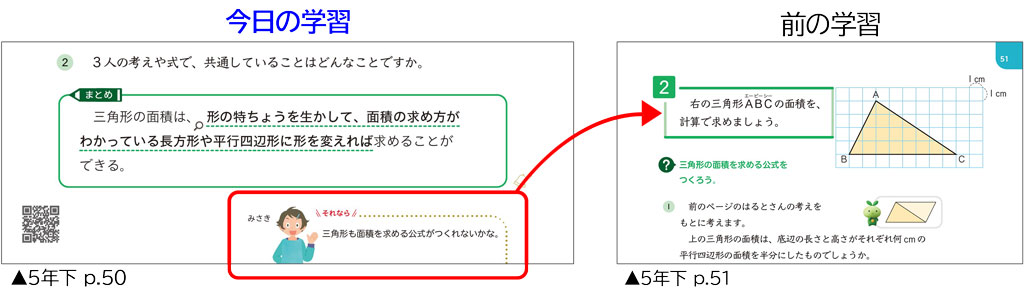
　まとめの後のみさきさんの吹き出しにご注目ください。ここでは、平行四辺形で求積公式をつくった経験から、”それなら三角形でも求積公式をつくれないか（つくれそうだ）”と促します。

統合的・発展的に考える力を育むことを願って

　このように、自ら学習をつないで問題を解決したり、新たな問題を見いだしたりする力を育むことを願い、新キーワードを付記しています。
　今回のキーワードは2年以上の様々な場面に朱文字で設置しています。ぜひ新キーワードが付記されている箇所にご注目ください。

　ここでご紹介した“ひみつ”以外にも「新編 新しい算数」の魅力はまだまだ他にもあります。ぜひバックナンバーもご覧ください。

「新編 新しい算数のひみつにせまる」バックナンバーは こちら

　令和6年度用教科書「新編 新しい算数」特設サイトでは、ここでご紹介した特長のほかにも新しい教科書の情報を掲載しています。ぜひ一度、サイトをご覧ください。

特設サイトは こちら