特集記事（小中学校）

前の学習とつなぐ。次の学習へのつながりをつくる。今も昔も変わることなく、先生方が大切にされてきた価値観です。
「新しい算数」でも大切にしてきた「つなぐ・つながる学び」を、6回に渡ってご紹介します。前回は、測定、変化と関係、データの活用領域における「今日の学習と次時の学習のつながり」を取り上げました。第5回の今回は、「1時間の授業の中で学びをつなぎ、深める授業」に注目します。

3上「大きい数のわり算、分数とわり算」p.116では、1時間の中で学びをつなぎ深めるために、まとめの後に補助発問を設定しています。

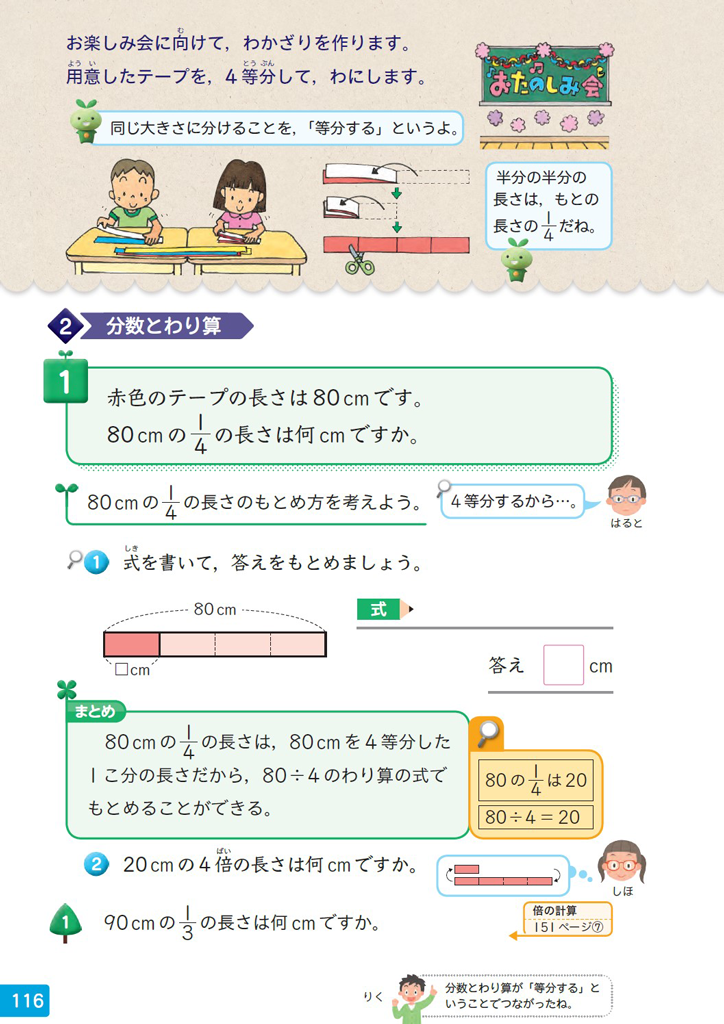
ここでは、80cmの \(\dfrac{1}{4}\) の長さを求めるとき、\(80\div 4\)のわり算で求めることができることをまとめた後、補助発問②で20cmの4倍の長さについて考え、倍と分数の関係について扱っていきます。

まとめの後に扱うことで、全体をもとにした見方だけでなく、部分をもとにした見方で2量の関係をとらえなおすことができ、わり算と分数、倍の関係の理解をより深めることができます。

1時間の中でも、まとめをして終わり、とするのではなく、本時で働かせた数学的な見方・考え方と既習を振り返るなど、発展的・創造的に学びをつなぐことを目指しています。

他にも、1時間の中でさらに理解を深めながら学びをつなぎ、深める補助発問は様々な箇所で設定しています。

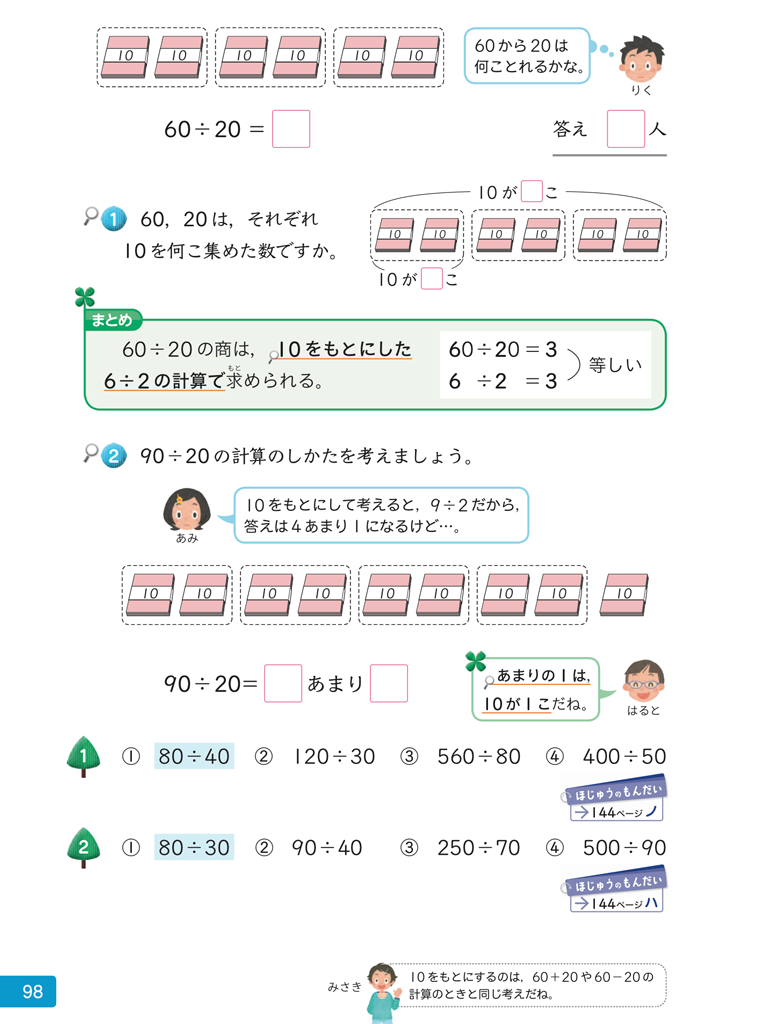
4上p.98では、\(60\div 20\) の計算が10をもとに計算できることをまとめた後、補助発問②で \(90\div 20\) を扱い、余りのある場合について考えていきます。まとめの後に扱うことで、10をもとに考えたことに立ち返り、\(9\div 2\) の余りの意味について考えることができます。

1時間の中でも学びをつなぎ、深める展開にすることで、\(60\div 20\)の計算で働かせた数学的な見方・考え方を振り返り、価値づけることを目指しています。

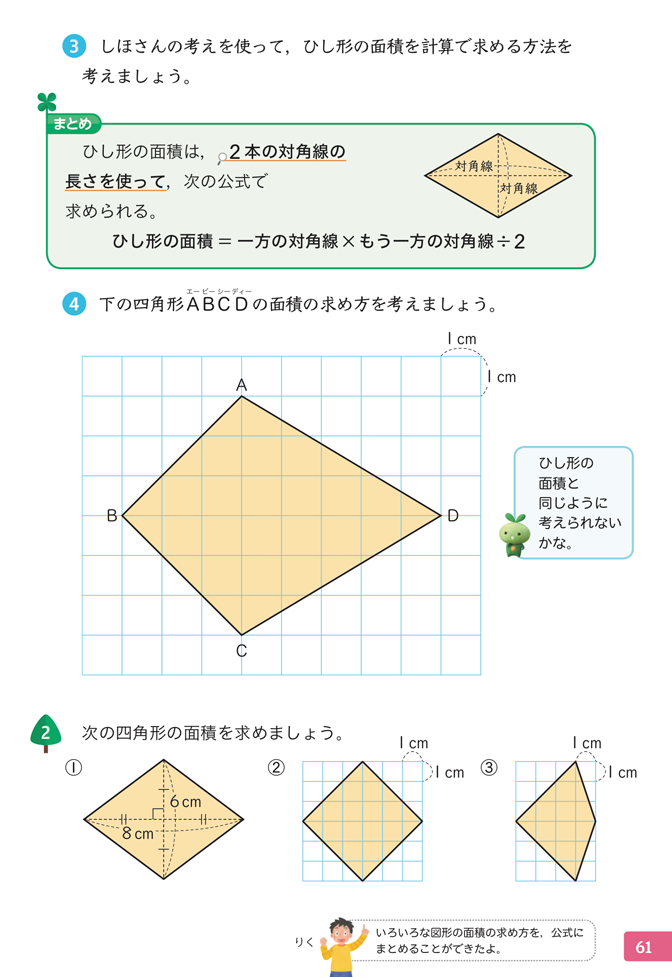
また5下p.61では、ひし形の求積公式をまとめた後、たこ形の図形の面積の求め方を考える補助発問④を設定しています。まとめの後にたこ形の求積を扱うことで、それぞれの図形の性質の共通点に着目し、ひし型の求積時に働かせた数学的な見方・考え方を振り返り、いっそう価値づけることができます。

このように、働かせた見方・考え方を振り返ったり、いかしたりしながら1時間の授業の中で学びをつなぎ、深めるための学習を「新しい算数」では大切にしています。

「つなぐ・つながる学び」については、情報誌math connect Vol.6でも特集しています。
ぜひ一度ご覧ください。